Лінійні перетворення

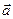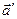Нехай задано векторний простір V_n і вектори і — деякі елементи цього простору.

Означення 10. Перетворення 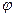, яке переводить кожен вектор 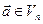у деякий вектор , такий що 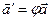, де вектор 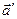є образом вектора 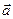, називається лінійним, якщо виконуються властивості:

1. 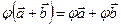. 2. .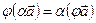

З означення випливає:

.

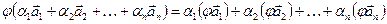Нехай у просторі V_n задано деякий базис:

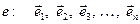. (1.13)

Будь-який вектор 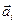у базисі (1.13) однозначно задається співвідношенням

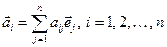. (1.14)

З координат векторів 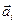у базисі (1.14) можна побудувати квадратну матрицю 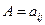, записавши координати векторів 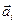як стовпці матриці А, тоді рівність (1.14) у матричному вигляді запишеться так:

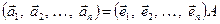. (1.15)

Матриця А задає лінійне перетворення j у базисі (1.13). Якщо через 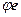позначимо рядок, складений з векторів бази, то з (1.14) і (1.15) випливає матрична рівність між лінійним перетворенням j і матрицею А в базисі е: 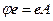. Знаючи матрицю А лінійного перетворення j в базисі (1.13), можна за координатами вектора 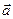в цьому базисі знайти координати його образу 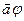за формулою 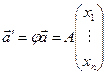, якщо 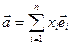. Стовпець координат вектора 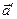(образу) дорівнює матриці А лінійного перетворення j, помноженій справа на стовпець координат вектора 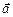. Якщо порівняти останню рівність з рівністю (1.12), очевидна повна їх аналогія, причому матриця Т була невиродженою.

Нехай маємо базиси 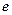і 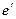у просторі V_n з матрицею переходу Т, тобто

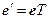, (1.16)

і нехай лінійне перетворення j задається в цих базисах відповідно матрицями А і А¢.

. (1.17)

Остання рівність (1.17) з урахуванням (1.18) записується у вигляді 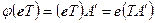. А проте 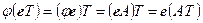. Тому, прирівнюючи праві частини, маємо: . Звідси на підставі лінійної незалежності базису і єдиності розкладу за базисом випливає: 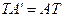. Матриця Т невироджена. Отже, існує Т^–1 і остаточно дістанемо співвідношення .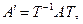

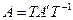Зауважимо, що квадратні матриці В і С називаються подібними, якщо вони пов’язані рівністю 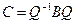, де Q — деяка невироджена квадратна матриця.

Таким чином, матриці, що задають одне й те саме лінійне перетворення в різних базисах, подібні між собою.

Нехай у просторі 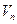задано лінійні перетворення 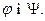Назвемо сумою цих перетворень перетворення 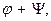якщо

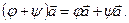
Добутком 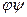назвемо перетворення, для якого виконується рівність 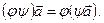Нарешті, добутком лінійного перетворення φ на число 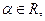є таке перетворення αφ, для якого

Легко показати, що перетворення є лінійними.

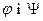Нехай у базисі перетворення задаються відповідно матрицями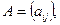 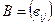, тобто

Тоді для векторів базису маємо:

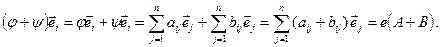
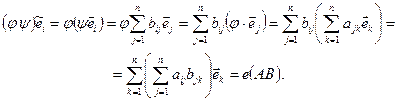
Отже, можна стверджувати, що матриця суми і добутку лінійних перетворень дорівнює відповідно сумі і добутку матриць цих перетворень в одному й тому самому базисі. А операції з лінійними перетвореннями мають ті самі властивості, що й операції з матрицями.