Основні поняття
ЛЕКЦІЯ 7-8. N-ВИМІРНИЙ ВЕКТОРНИЙ ПРОСТІР
ПЛАН
1. Основні поняття
2. Зв’язок між базисами
3. Лінійні перетворення
4. Власні числа і власні вектори матриці
Основні поняття
Означення 1. Сукупність упорядкованих систем з n дійсних чисел, для яких визначено дії додавання і множення на число, утворює n-вимірний векторний простір Vn.
Елементами заданого таким чином простору будуть впорядковані системи чисел, які називатимемо n-вимірними векторами і записуватимемо: 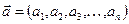 . Числа ai, i = 1, 2, 3, ..., n називаються компонентами вектора
. Числа ai, i = 1, 2, 3, ..., n називаються компонентами вектора 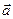 . Якщо розглянути ще один елемент простору Vn — вектор
. Якщо розглянути ще один елемент простору Vn — вектор 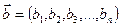 , то у просторі Vn можна виконувати такі дії.
, то у просторі Vn можна виконувати такі дії.
Додавання двох векторів за правилом:
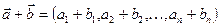 .
.
Множення вектора на число a, 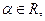 за правилом:
за правилом:
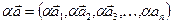 .
.
Означення 2. Два вектори 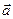 і
і 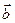 вважаються рівними, якщо виконуються рівності
вважаються рівними, якщо виконуються рівності 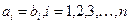 .
.
Роль нуля відіграє 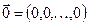 . З означень дій додавання і множення вектора на число випливають властивості:
. З означень дій додавання і множення вектора на число випливають властивості:
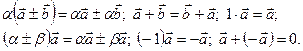
Означення 3.Вектор 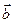 називається лінійною комбінацією векторів
називається лінійною комбінацією векторів 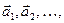
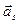 , якщо існують такі числа
, якщо існують такі числа 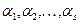 , що
, що 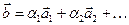
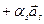 .
.
Означення 4. Система векторів 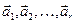 називається лінійно залежною, якщо існують такі числа
називається лінійно залежною, якщо існують такі числа 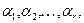 хоча б одне з яких відмінне від нуля, що виконується рівність
хоча б одне з яких відмінне від нуля, що виконується рівність
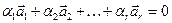 . (1.1)
. (1.1)
Означення 5. Система векторів 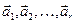 називається лінійно незалежною, коли всі
називається лінійно незалежною, коли всі 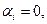
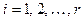 , що виконується рівність
, що виконується рівність
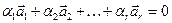 .
.
Постає запитання: а чи існують взагалі системи лінійно незалежних векторів? Розглянемо систему векторів в n-вимірному просторі Vn:
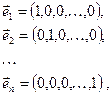
яку далі називатимемо одиничною системою векторів. Покажемо, що така система векторів лінійно незалежна. Для цього утворимо лінійну комбінацію: 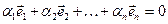 . Ліва частина цієї рівності є вектор
. Ліва частина цієї рівності є вектор 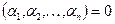 . Звідси випливає, що всі
. Звідси випливає, що всі 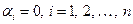 .
.
Згодом побачимо, що у просторі Vn існує безліч лінійно незалежних систем векторів.
Сформулюємо таке важливе твердження.
Дата добавления: 2015-10-05; просмотров: 1000;
