Власні числа і власні вектори матриці

Нехай 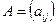— деяка квадратна матриця розміру 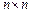з дійсними елементами, 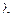— деяке невідоме число. Тоді матриця 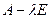, де Е — одинична матриця, називається характеристичною матрицею для матриці А:

.

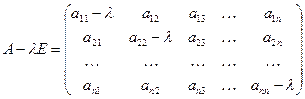Поліном n-го степеня 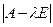називається характеристичним поліномом матриці А, а його корені – власними числами матриці А.

Можна стверджувати, що подібні матриці мають однакові характеристичні поліноми і, як наслідок, однакові власні числа.

Наслідок. Лінійне перетворення j в різних базисах має різні матриці, але всі вони мають однакові власні числа. Тому можна стверджувати, що лінійне перетворення j характеризується набором власних чисел, які далі називатимемо спектром лінійного перетворення j, або спектром матриці А.

Розглянемо лінійне перетворення j у просторі V_n, таке що переводить відмінний від нуля вектор 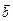у вектор, пропорційний до самого вектора :

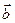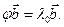(1.19)

Такий вектор 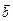називатимемо власним вектором перетворення j, а 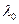— власним числом, що відповідає цьому власному вектору.

Розглянемо тепер задачу відшукання такого базису для лінійного перетворення j, в якому б його матриця мала найпростіший діагональний вигляд.

Вважатимемо, що лінійне перетворення j має такий характеристичний поліном, що всі його корені дійсні і різні. Тобто, розв’язавши рівняння n-го порядку 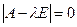, знайдемо n різних дійсних коренів 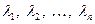. Якщо виконується така умова, то лінійне перетворення j дійсного лінійного простору V_n має простий спектр.

Кожному власному числу lі відповідає певний власний вектор. Власних векторів у цьому разі буде також n. Вони утворюють лінійно незалежну систему векторів. Їх можна розглядати як базис Vn, в якому матриця лінійного перетворення A набирає найпростішого діагонального вигляду.