Арифметические операции над двоичными числами
Над двоичными числами можно выполнять те же арифметические операции, что и с обычными числами, но в соответствии со следующими правилами двоичной арифметики:
| сложение | вычитание | умножение |
| 0 + 0 = 0 | 0 - 0 = 0 | 0 * 0 = 0 |
| 0 + 1 = 1 | 1 - 0 = 1 | 0 * 1 = 0 |
| 1 + 0 = 1 | 1 - 1 = 0 | 1 * 0 = 0 |
| 1 + 1 = 10 | 10 - 1 = 1 | 1 * 1 = 1 |
Сложение чисел независимо от системы счисления выполняется поразрядно, начиная с младшего. Если при сложении цифр одного разряда сумма равна основанию системы счисления, образуется единица переноса в соседний старший разряд, а в разряде суммы записывается нуль. В случае сложения двух единиц разряда с единицей переноса из младшего разряда, образуется единица переноса в старший разряд, а в разряде суммы записывается единица.
Действия двоичной арифметики можно проверить, если перевести все операнды (слагаемые и сумму и т.д.) в десятичную систему счисления.
При вычитании в данном разряде из нуля необходимо занять единицу из соседнего старшего разряда, которая равна двум единицам данного разряда.
Пример 4.9. Найти разность A-B, где A=1011,0012 ; B=1001,101 2 .
Запишем исходные числа в столбик.
|
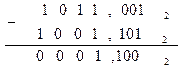
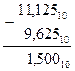
Умножение двоичных многоразрядных чисел производится путем образования частичных произведений и последующего их суммирования. В соответствии с таблицей двоичного умножения каждое частичное произведение равно нулю, если в соответствующем разряде множителя стоит ноль, или равно множимому, сдвинутому на соответствующее число разрядов влево, если в разряде множителя стоит единица. Таким образом, операция умножения многоразрядных чисел сводится к операциям сдвига и сложения. Положение запятой определяется также, как при умножении десятичных чисел.
Пример 4.10. Умножить 1011,12*101,01 2
|
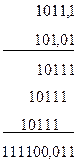
Деление чисел производится по правилам умножения и вычитания, как и в десятичной системе счисления. Особенности выполнения деления двоичных чисел поясняются примером:
Пример 4.11.Найти частное от деления А на В, где А = 100011,112, В=110,12.
1000111,1| 1101
1101 101,1
1101
11 01
11 01
Проверка
35,7510:6,510=5,5 10
Деление начинается с того, что в делимом и делителе запятая переносится вправо на одинаковое количество разрядов так, чтобы делитель стал целым числом. Затем от делимого слева отделяется минимальная группа разрядов, которая, рассматриваемая как число, превышает или равна делителю. Дальнейшие действия выполняются по обычным правилам, причем последняя цифра частного получается тогда, когда все цифры делимого исчерпаны, либо когда достигнута заданная точность.
Дата добавления: 2015-10-13; просмотров: 1502;
