Зауваження до аксіоми I
Аксіома I у списку аксіом стереометрії набуває іншого змісту, ніж вона мала у планіметрії. У планіметрії ця аксіома стверджує існування точок поза даною прямою на площині, у якій лежить пряма. Саме в такому розумінні ця аксіома застосовувалася у процесі побудови геометрії на площині. Тепер ця аксіома стверджує взагалі існування точок, що не лежать на даній прямій. З неї безпосередньо не випливає, що існують точки поза даною прямою на площині, у якій лежить пряма. Це потребує спеціального доведення. Дамо таке доведення.
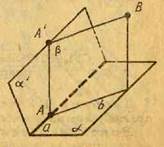 Нехай α — площина і а — пряма в цій площині (рис. 7). Доведемо існування точок у площині α, що не лежать на прямій а. Позначимо точку А на прямій а і точку А' поза площиною α. Через пряму а і точку А' проведемо площину α '.
Нехай α — площина і а — пряма в цій площині (рис. 7). Доведемо існування точок у площині α, що не лежать на прямій а. Позначимо точку А на прямій а і точку А' поза площиною α. Через пряму а і точку А' проведемо площину α '.
Візьмемо точку В поза площиною α' і проведемо через пряму АА' і точку В площину β. Площини α і β перетинаються по прямій b, що проходить через точку А и відмінна від прямої а. Точки цієї прямої, відмінні від А, лежать у площині α поза прямою а, що й треба було довести.
Рис. 7
Мал.7
Дата добавления: 2015-10-19; просмотров: 1067;
