Існування площини, що проходить через три дані точки
Теорема 1.3. Через три точки, що не лежать на одній прямій, можна провести площину, і тільки одну.
Доведення. Нехай А, В, С — три дані точки, що не лежать на одній прямій (рис. 6). Проведемо прямі АВ і АС; вони різні, тому що точки А, В, С не лежать на одній прямій. За аксіомою С3 через прямі АВ і АС можна провести площину α. Ця площина містить точки А, В, С.
Доведемо, що площина α, що проходить через точки А, В, С, єдина. Дійсно, площина, що проходить через точки А, В, С, за теоремою 1.2 містить прямі АВ і АС. А за аксіомою С3 така площина єдина.
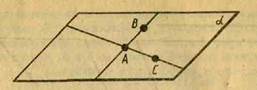 |
Мал.6
Дата добавления: 2015-10-19; просмотров: 1139;
