Задание 23.

Какие отношения между фигурами устанавливают, и какие опе­рации над фигурами выполняют дошкольники, получив следующие задания:

а) Нарисуй круг и квадрат так, чтобы:

- круг находился в квадрате (рис.37),

- квадрат находился в круге (рис.38),

- квадрат и круг пересекались (рис.39),

- квадрат и круг не пересекались (рис.40).

Рис. 37 Рис. 38 Рис. 39 Рис. 40

б) Закрась:

- часть фигуры между границей круга и квадрата (рис.41);

- общую часть фигур (рис.42);

- всю фигуру, которая получилась (рис.43).

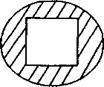
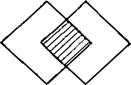
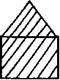
Рис.41 Рис. 42 Рис. 43

Свойства геометрических фигур изучает наука геометрия.

Планиметрия - часть геометрии, изучающая фигуры на плос­кости.

Стереометрия - часть геометрии, изучающая фигуры в про­странстве.

Дошкольники знакомятся с плоскими и пространственными фигурами, учатся устанавливать между ними связи (куб – квад­рат, шар – круг,...).

Геометрическая фигура называется плоской, если все точки фигуры принадлежат одной плоскости. На плоскости различают выпуклые и невыпуклые фигуры.

Геометрическая фигура называется выпуклой, если она цели ком содержит отрезок, концами которого служат любые две точки, принадлежащие фигуре (рис.44).

Выпуклые Невыпуклые

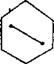
Рис. 44

При обучении дошкольников мы не даем явных определений фигур, а знакомим с их внешним видом, названием, свойствами, отношением равенства между фигурами.

Геометрия Евклида (древнегреческий ученый, III в. до н.э.), которую мы изучаем, построена по такому принципу:

1. Часть понятий вводится без определения (точка, прямая, плоскость ...). Другие понятия определяются, как правило, через род и видовое отличие.

2. Часть свойств фигур вводится через аксиомы. (Например, через две точки можно провести единственную прямую.)

3. Другие свойства фигур формулируются в виде теорем и доказываются с использованием аксиом и ранее доказанных теорем.