Рівняння пресування по Куніну і Юрченко
Серед рівнянь пресування, виведених різними авторами, багато одержаниі емпірично, тобто шляхом математичної обробки експериментальних даних. В цьому відношенні є типовим рівняння по Н. Ф. Куніну і В. Д. Юрченко.
Своє рівняння пресування автори одержали математичною обробкою експериментальних даних, отриманих при ущільненні пластичних і крихких порошків (  , графіту, селітри, кам'яної солі і ін.). Побудовані залежності показали, що для всіх досліджуваних матеріалів при збільшенні тиску пресування р об'єм матеріалу, що ущільнювався
, графіту, селітри, кам'яної солі і ін.). Побудовані залежності показали, що для всіх досліджуваних матеріалів при збільшенні тиску пресування р об'єм матеріалу, що ущільнювався 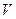 , зменшується, а щільність
, зменшується, а щільність 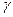 збільшується. У вузькому інтервалі тиску збільшення щільності пропорційне початковій щільності і приросту тиску
збільшується. У вузькому інтервалі тиску збільшення щільності пропорційне початковій щільності і приросту тиску 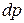 :
:
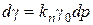 , (2.117)
, (2.117)
де 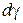 – збільшення густини при прирості тиску на величину
– збільшення густини при прирості тиску на величину 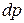 ;
;
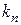 – множник пропорційності,
– множник пропорційності, 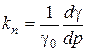 , який показує відносну зміну щільності на одиницю тиску;
, який показує відносну зміну щільності на одиницю тиску;
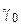 – насипна щільність.
– насипна щільність.
Оскільки,  , то автори пропонують ввести поняття коефіцієнта пропорційності, або коефіцієнта пресування:
, то автори пропонують ввести поняття коефіцієнта пропорційності, або коефіцієнта пресування:
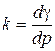 (2.118)
(2.118)
і використовувати його надалі при висновку рівняння пресування.
Побудовані на підставі експериментальних даних залежності  і
і 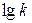 від тиску пресування мають однаковий вигляд для всіх ущільнюваних матеріалів (рис.31).
від тиску пресування мають однаковий вигляд для всіх ущільнюваних матеріалів (рис.31).
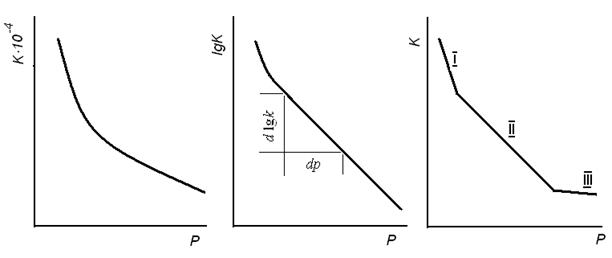

а б в
Рисунок 31 – Залежність коефіцієнта пресування  і
і 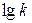 від тиску пресування
від тиску пресування
Проводячи аналіз одержаних залежностей, можна дійти висновку, що весь процес ущільнення можна розбити на три стадії (області) пресування. У кожній з них протікають процеси, відмінні один від одного (рис.31, в).
На першій стадії пресування (ділянка I, рис. 31) відбувається зближення і ущільнення частинок без їх деформації – ділянка підпресовування. На другій стадії (ділянка II) відбуваються пластична і крихка деформації частинок, взаємне їх обтікання, заповнення міжкристалітних проміжків і утворення компактного тіла.
На третій стадії (ділянка III ) відбувається об'ємне стиснення компактного тіла, що утворилося. При переході від першої області ущільнення до другої і третьої зменшується коефіцієнт пресування, тобто швидкість ущільнення матеріалу.
Для практики найважливіше значення має друга область, де відбувається основне формування властивостей пресовок.
Як видно з рисунку 31, а, залежність  від
від  визначається деякою функцією, яка для другої області має експоненціальний хід. Підтвердженням цього є залежність
визначається деякою функцією, яка для другої області має експоненціальний хід. Підтвердженням цього є залежність 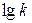 від
від  (рис.31, б), яка в інтервалі практичного тиску виражається прямими лініями, тобто
(рис.31, б), яка в інтервалі практичного тиску виражається прямими лініями, тобто
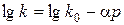 , (2.119)
, (2.119)
або
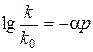 , (2.120)
, (2.120)
або після потенціювання
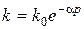 (2.121)
(2.121)
де 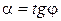 (
( 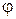 – кут нахилу прямих на рисунку 31, б до осі абсцис);
– кут нахилу прямих на рисунку 31, б до осі абсцис);
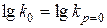 , тобто значення
, тобто значення 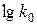 отримуємо при перетині прямих на рисунку 31, б з віссю ординат.
отримуємо при перетині прямих на рисунку 31, б з віссю ординат.
Якщо узяти елементарну ділянку на прямій (рис. 31, б), то можна записати
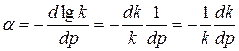 . (2.122)
. (2.122)
Виходячи з цього можна сказати, що коефіцієнт характеризує відносне зменшення коефіцієнта пресування при зміні тиску на одиницю. Іншими словами, його можна назвати коефіцієнтом втрати стисливості. Для даного матеріалу за одних і тих же умов пресування він постійний.
З виразів (139) і (140), одержимо диференціальне рівняння пресування по Куніну і Юрченко:
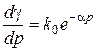 . (2.123)
. (2.123)
Або, інтегруючи його:
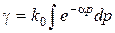 (2.124)
(2.124)
Приймаючи, що 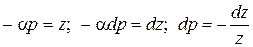 , одержуємо
, одержуємо
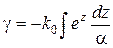 або
або 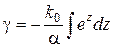 .
.
Або після інтегрування:
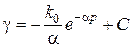 . (2.125)
. (2.125)
Якщо прийняти, що рівняння (147) справедливе до нескінченно великого тиску і щільності 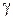 при цьому нескінченно великому тиску рівна
при цьому нескінченно великому тиску рівна 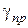 (гранична щільність), то при
(гранична щільність), то при 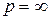 і
і 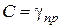 . Тоді рівняння (2.125) прийме вигляд:
. Тоді рівняння (2.125) прийме вигляд:
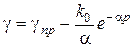 . (2.126)
. (2.126)
Рівняння (2.126) являє собою закон пластичного пресування порошкоподібних тіл в інтегральній формі. У нього входять три константи (параметра), які характеризують матеріал, який ущільнюється: 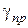 – умовна гранична щільність;
– умовна гранична щільність; 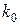 – початковий коефіцієнт пресування, г/(кг∙см);
– початковий коефіцієнт пресування, г/(кг∙см); 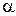 – коефіцієнт втрати стисливості, см2/кг.
– коефіцієнт втрати стисливості, см2/кг.
Умовна гранична щільність 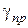 чисельно рівна тій щільності, яка досягається при нескінченно великому тиску. Насправді рівняння (2.126) відображає процес пресування тільки в так званій "пластичній області", де ущільнення відбувається за рахунок пластичної і крихкої деформації частинок порошку. У зв'язку з цим екстраполяція на нескінченно великий тиск носить чисто умовний характер і це робиться для зручності визначення постійної в рівнянні (2.126) при інтегруванні диференціального рівняння.
чисельно рівна тій щільності, яка досягається при нескінченно великому тиску. Насправді рівняння (2.126) відображає процес пресування тільки в так званій "пластичній області", де ущільнення відбувається за рахунок пластичної і крихкої деформації частинок порошку. У зв'язку з цим екстраполяція на нескінченно великий тиск носить чисто умовний характер і це робиться для зручності визначення постійної в рівнянні (2.126) при інтегруванні диференціального рівняння.
Не дивлячись на те, що 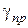 визначається екстраполяцією, вона достатньою мірою відображає властивості пресованого матеріалу в другій області.
визначається екстраполяцією, вона достатньою мірою відображає властивості пресованого матеріалу в другій області.
Якби рівняння (2.126) було справедливе до нескінченно великого тиску, то 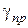 повинна б дорівнювати густині монокристала. Насправді ж вона виявляється дещо вищою.
повинна б дорівнювати густині монокристала. Насправді ж вона виявляється дещо вищою.
При розрахунках процесу пресування необхідно знати значення 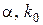 і
і 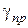 . Один з шляхів їх визначення – складання системи трьох рівнянь з трьома невідомими. Для цього визначається густина пресовок при трьох тисках. Рішення цих рівнянь дає шукані величини. У зв'язку з тим, що рівняння типу (2.126) дещо складні для сумісного вирішення, зручніше користуватися графічним способом.
. Один з шляхів їх визначення – складання системи трьох рівнянь з трьома невідомими. Для цього визначається густина пресовок при трьох тисках. Рішення цих рівнянь дає шукані величини. У зв'язку з тим, що рівняння типу (2.126) дещо складні для сумісного вирішення, зручніше користуватися графічним способом.
Для цього на підставі експериментальних даних будується графік в координатах 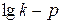 (рис.31, б) і з нього визначається коефіцієнт втрати здатності до стискання:
(рис.31, б) і з нього визначається коефіцієнт втрати здатності до стискання:
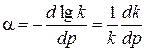 .
.
Знаючи 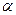 і
і 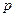 визначають величину
визначають величину 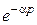 і будують графічну за\
і будують графічну за\
]’
]ежість в координатах 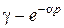 (рис. 32).
(рис. 32).

|
| Рисунок 32 – До визначення постійних в рівнянні (148) |
Якщо тиск і щільність при випробуваннях відповідають області пластичного пресування, то всі крапки знаходитимуться на одній прямій. Продовження цієї прямої до перетину з віссю ординат дає значення 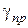 .
.
Тангенс кута нахилу прямої до осі абсцис рівний відношенню 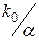 . Знаючи
. Знаючи 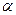 , знаходимо
, знаходимо 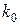 .
.
Розглянуте рівняння Н. Ф. Куніна і В. Д. Юрченка описує з достатнім ступенем точності процес пресування тільки тих порошків, для яких воно було виведене, що є істотним недоліком.
Дата добавления: 2015-09-07; просмотров: 1027;
