Рівняння пресування по Ждановичу

При виведенні своїх рівнянь Г.М. Жданович використовував два підходи. У одному випадку він виводить рівняння виходячи з рішення контактної задачі на підставі уявлень про деформаційний механізм ущільнення порошкового тіла.

Як було встановлено ним , зусилля пресування 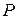розглядається як сума проекцій опорних контактних сил всіх частинок перетину пресовки відповідно до рівняння (2.40):

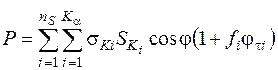
або при переході до середньостатистичних величин відповідно до рівняння (2.41):

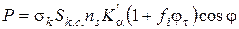
Беручи до уваги, що середньостатистичне число частинок даного шару пресування 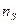відповідно до (2.19)

,

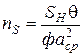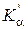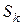а і відповідно до (2.26) і (2.27):

; ,

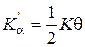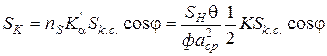Визначаємо ,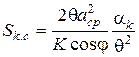

де 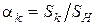– безрозмірна відносна величина проекції сумарної контактної поверхні пресування в даний момент пресування.

Підставивши значення (2.19), (2.26) і (2.28) в (2.41) і розділивши його на 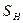, одержимо вираз для тиску пресування:

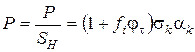(2.58)

або з урахуванням того, що, ,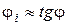

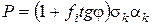, (2.59)

По Ждановичу контактна напруга для пластичних металів з урахуванням їх зміцнення при деформації в процесі ущільнення порошкового тіла пов'язано з відносною щільності пресовки залежністю

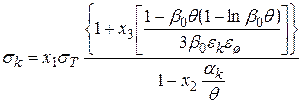, (2.60)

де 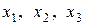– постійні коефіцієнти, залежні від фізичних властивостей матеріалу частинок;

;

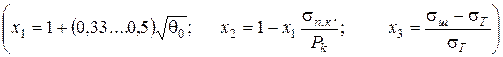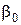– відносний об'єм пресування в початковий момент пресування (відносний об'єм насипки);

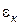– приведена відносна деформація пресовки при 100%-й щільності пресовки;

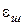– відносна деформація, відповідна початку утворення шийки між частинками при їх деформації при ущільненні;

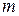*– показник зміцнення.

Для крихких матеріалів, 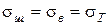, а 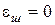, тому

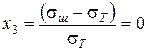(2.61)

і, отже, контактна напруга 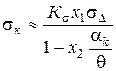, (2.62)

де .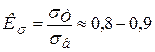

Підставляючи значення з (2.60) і (2.62) в (2.59), одержуємо рівняння для визначення тиску пресування порошків пластичних (2.63) і крихких (2.64) матеріалів:

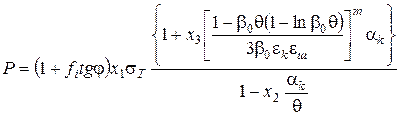(2.63)

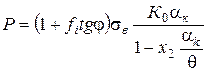, (2.64)

У ці рівняння входять змінні величини, 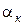, 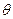і 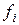, що утрудняє їх практичне використання. У зв'язку з цим Жданович запропонував інтерполяційне рівняння:

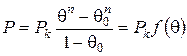, (2.65)

де 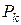– тиск, необхідний для 100%-го ущільнення порошкового тіла;

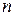– показник ступеня, який необхідно визначити.

Для цього розглянемо спільно вирази (2.63), (2.64) і (2.65) і одержимо для випадку ущільнення порошків з пластичних матеріалів ( ):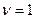

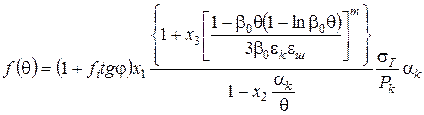(2.66)

для крихких ( ):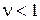

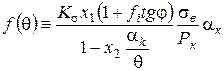. (2.67)

Інтерполяційна форма вибрана Ждановичем таким чином, що при певному значенні показника ступеня 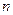може бути досягнутий достатньо високий ступінь наближення. Видно, що початкова і критична краєві умови дотримуються при будь-яких кінцевих значеннях показника ( ).

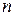Якщ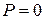о, , то ,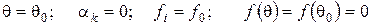

а якщ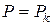о , то .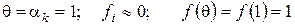

У зв'язку з цим показник ступеня доцільно визначати при деякому середньому значенні відносної щільності пресовки .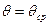

Як середнє значення 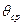приймається середня геометрична щільність пресовк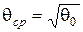и . При 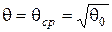матимуть місце співвідношення:

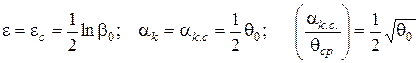. (2.68)

З урахуванням співвідношень (2.68) залежності (2.66) і (2.67) приймуть вигляд

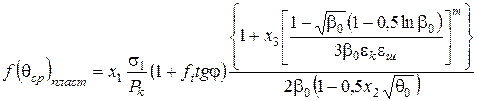; (2.69)

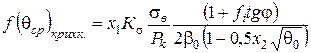. (2.70)

З інтерполяційної формули (85) виходить, що:

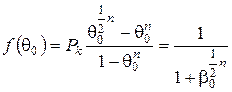(2.71)

Вирішуючи цей вираз відносно 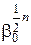, одержуємо:

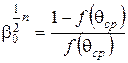(2.72)

Далі вирішуючи вираз (2.72) знаходимо:

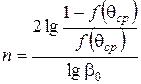(2.73)

Таким чином, аналізуючи одержаний вираз (2.73), слід зазначити, що показник ступеня 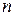залежить від механічних властивостей порошку 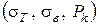коефіцієнт контактного тертя 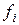, відносної густини насипання порошкового тіла ( 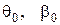), тобто практично від всіх чинників, що мають вплив на процес ущільнення порошкових матеріалів.

Остаточне рівняння пресування, одержане Ждановичем має вигляд:

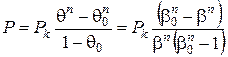, (2.74)

або відносно 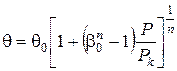(2.75)

По Ждановичу можливий також інший підхід до рішення задачі про оптимальний тиск пресування. Оскільки пресування – складний процес пружно-пластичної деформації великого числа частинок, при якому і відносне розташування частинок, і картина їх взаємодії безперервно змінюються, виведення рівняння може бути обгрунтоване виходячи не з деформації одиночного шару частинок, а з поведінки такої частини об'єму порошкового тіла, що складається з частинок з середнім розміром 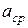, яка характеризує і зберігає всі фізичні властивості даного тіла, що знаходиться під тиском. Оскільки розмір пресованого виробу в більшості випадків більше 30 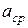, то можна застосувати гіпотезу суцільності.

У цьому випадку виведення рівняння пресування Жданович засновує на наступному:

1 Процес пресування порошкового тіла розглядається як процес пружно-пластичної деформації деякого умовного суцільного тіла, яке в процесі деформації зміцнюється і змінює свої розміри.

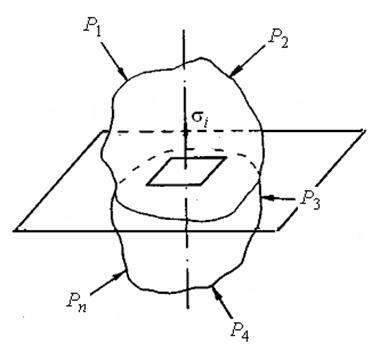
2Частинка порошку (рис. 24), виділена з пресовки, що знаходиться під середнім тиском пресування ( 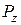) у даному перетині брикета, перебуває в рівновазі під дією системи сил, прикладених в місцях контакту – .

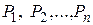Під дією зовнішніх сил в тілі частинки виникають внутрішні сили. Нормальна складова напружень, створених внутрішніми силами в кожній точці частинки може бути визначена: 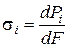(2.76)

де 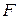– площа поперечного перетину даної частинки в площині, перпендикулярній до напряму руху пуансона – осі .

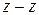Рисунок 24 – Частина порошкового тіла, що знаходиться в рівновазі під дією зовнішніх сил

З урахуванням гіпотези суцільності передбачається, що фізичні всіх частинок однакові. Тоді напруження 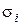, створені внутрішніми силами в даному перетині уздовж осі 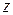, будуть постійними, отже, виконуватиметься рівність

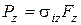, (2.77)

де 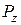– зусилля преса;

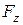– площа "металевого" перетину пресовки при зусиллі пресування .

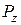Щоб перейти до тиску пресування 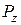, обидві частини рівняння (2.77) необхідно розділити на площу перетину брикета :

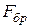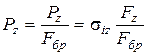, (2.78)

звідки

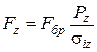. (2.79)

Оскільки із зростанням 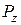збільшуються 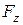і 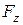, то рівняння можна записати в диференціальній формі:

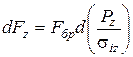, (2.80)

тобто зміна площі металевого перетину прямо пропорційна зміні відношення .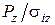

3 Відношення площі металевого перетину до номінальної площі

пресовки Жданович називає фактором суцільності :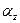

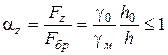, (2.81)

де 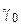– початкова щільність брикета;

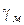– густина компактного матеріалу;

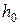– початкова висота брикета;

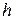– поточна висота брикета.

4Процес деформації пористого брикета супроводжується зміцненням, яке пов'язане із збільшенням щільності і зростанням контактної поверхні, наклепом частинок, і, отже, із збільшенням опірності деформації. Весь цей процес називається процесом сумарного приведеного, або ефективного зміцнення брикета.

Як критерій такого зміцнення може служити статична функція від чинника суцільності:

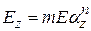, (2.82)

де 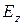– модуль зміцнення пресування при тиску Р;

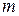– коефіцієнт пропорційності, що враховує фізичні властивості матеріалу порошку, обумовлені способом його отримання;

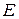– модуль пружності матеріалу порошку;

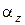– чинник суцільності;

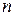– показник зміцнення.

Підставивши у вираз (103) значення 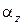з (102), знаходимо

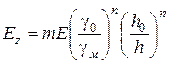(2.83)

5Внутрішні напруження в брикеті прямо пропорційні модулю зміцнення брикета і його відносної деформації:

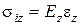, (2.84)

або

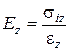, (2.85)

де ,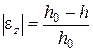

або в диференціальній формі

d 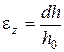. (2.86)

Знак "–" вказує на те, що приріст внутрішньої напруги пропорційний негативній зміні висоти пресовки.

Тоді

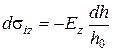. (2.87)

6 Враховуючи, що 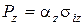, і рівняння (2.83) (2.85), можна записати

,

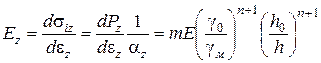або

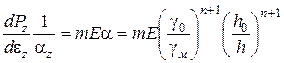. (2.88)

Вирішуючи спільно рівняння (109) і (107), знаходимо:

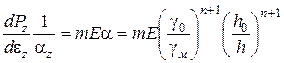. (2/89)

Отже, 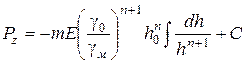. (2.90)

Інтегруючи вираз (111), одержимо

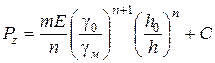. (2.91)

Аналізуючи вираз (2.91), помічаємо, що при . Тоді

.

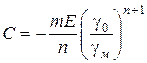Підставивши значення постійної інтегрування у вираз (2.91) одержимо

,

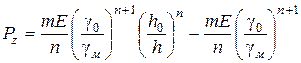або 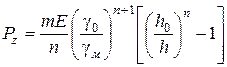. (2.92)

Проводячи подальший аналіз, відзначаємо, що при ,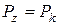

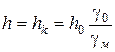де 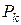– критичний тиск пресування, відповідне 100%-й щільності пресовки, який дорівнює напрузі витікання (течії) максимально зміцненого матеріалу, причому для даного металу ;

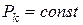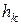– приведена, або критична, висота пресовки, відповідна 100%-й щільності.

Підставивши у вираз (2.92) значення 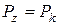і 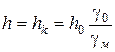і вирішуючи його відносно 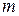, одержимо

,

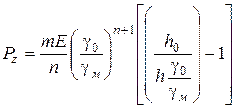звідки 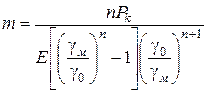. (2.93)

Далі, підставивши значення в рівняння (113), одержимо:

,

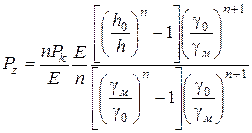або після спрощення 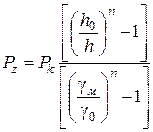. (2.94)

Вирішуючи рівняння (2.94) відносно 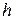, одержуємо

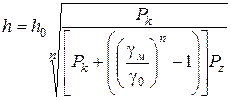. (2.95)

Рівняння (2.94) і (2.95) при 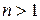є деякими гіперболічними функціями вищого порядку, що відображають кількісні закономірності процесу пресування металевого порошку у всьому інтервалі тиску пресування від 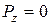до 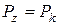(рис.25).

Аналіз рівнянь Ждановича показує, що вони справедливі у всьому інтервалі тиску. Проте рівняння було виведене виходячи з припущення, що відсутнє тертя об стінки прес-форми.

Для того, щоб скористатися рівнянням в практиці з урахуванням сил зовнішнього тертя об стінки прес-форми, необхідно мати в своєму розпорядженні закономірність зміни середнього тиску пресування 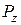по висоті пресовки (функція ).

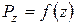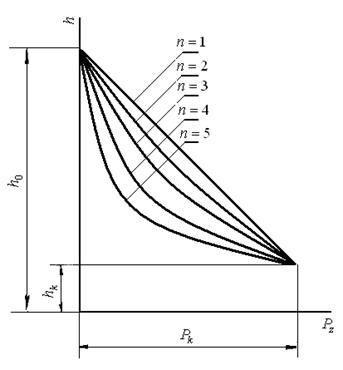
Аналіз напруженого стану ущільнюваного елементу об'єму дозволив Ждановичу одержати цю залежність (рис.26):

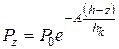, (2.96)

де 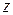– відстань від дна прес-форми до даного перетину пресування.

Рисунок 25 – Графічний вид рівняння (2.95)

Аналіз рівняння (2.96) і (рис.26) дає можливість дійти висновку, що у будь-який момент пресування тиск нетто рівний середньому тиску на неробочому (нижньому) пуансні:

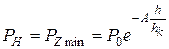, (2.97)

де 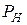– зусилля, що необхідне для пресування без урахування сил зовнішнього тертя;

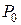– загальне необхідне зусилля з урахуванням втрат на зовнішнє тертя.

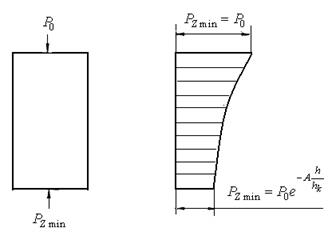
Рисунок 26 – Графічний вид рівняння (2.96)

Враховуючи вираз (2.96), рівняння пресування можна записати у вигляді

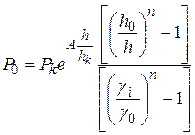,(2.98)

або відносно h

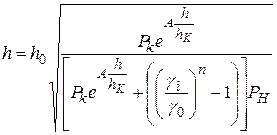. (2.99)

У рівняннях (2.98) і (2.99)

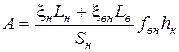, (2.100)

де 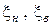– коефіцієнт бічного тиску відповідно на зовнішню і внутрішню бічну поверхню пресування (додаток 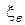пропадає у разі відсутності останньої);

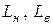– довжина параметрів або контурів відповідно зовнішньої і внутрішньої бічних поверхонь пресування;

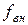– коефіцієнт зовнішнього тертя пресування об стінки прес-форми; 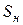– номінальна площа перетину пресування.

Величина 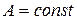, проте, якщо одна з величин 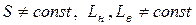, то і .

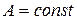Для остаточного використання рівнянь (2.94), (2.95), (2.98), (2.99) необхідно визначити величини 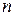і 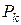. Показник 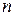може бути обчислений за формулою (2.73) або визначений експериментально. Для порошків багатьох металів ( 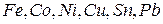) він трохи відрізняється від значення 4. У зв'язку з цим при розрахунках можна приймати 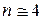з внесенням при цьому помилки 5–8%)

Величина 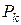визначається на практиці шляхом пресування дослідних зразків в малогабаритній прес-формі.

При цьому використовується вираз (2.97), звідки

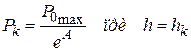(2.101)