Рівняння пресування по Бальшину

При математичному описі процесу пресування, тобто з'ясуванні кількісної закономірності зміни щільності порошкового тіла від тиску пресування, часто використовують спрощений підхід, приймаючи при виведенні рівнянь пресування певні допущення. До таких рівнянь слід віднести одне з перших в теорії пресування порошкових матеріалів, запропоновані М.Ю. Бальшиним. При виведенні своїх рівнянь він зробив наступні допущення.

1 Деформація порошкових тіл подібно компактним, тобто якщо зусилля пресування віднести до площі контактного перетину, то межа міцності або межа текучості не залежатиме від пористості і буде однаковою як для пористого, так і для компактного тіла.

2 Деформація частинок підпорядковується закону Гука аж до досягнення межі текучості.

3 Контактна поверхня змінюється тільки внаслідок пластичної деформації частинок, оскільки при відносно високому тиску пресування приростом контактної поверхні завдяки переміщенню частинок одина відносно одної можна знехтувати.

4 Нагартування матеріалу частинок, в процесі пресування відсутній, внаслідок чого на контактних ділянках критична напруга ( 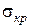) залишається постійною.

Крім того, М. Ю. Бальшин також допускає, що сумарна відносна деформація частинок в контактних ділянках рівна відносній зміні висоти брикета. Приймається також, що площа пресування дорівнює 1 см² і замість зусилля пресування можна використовувати тиск пресування.

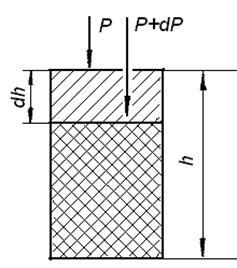
Схема пресування по М.Ю. Балишину показана на рисунку 27.

Передбачається, що в циліндровій прес-формі ущільнюється пресовка з приведеною висотою 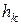. Під навантаженням Р вона має висоту h. При збільшення тиску на dP висота зменшується на величину dh.

В цьому випадку напруга в порошковоій пресовці визначається діленням приросту тиску на площу контактного перетину S_k, тобто залежність має такий же вигляд, як і у разі пружної деформації компактного металу, що підкоряється закону Гука:

Рисунок 27 – Схема пресування по Бальшину

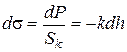, (2.102)

де 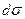– приріст напруги;

dP – приріст навантаження;

S_k – площа контактного перетину;

k_ч – постійний коефіцієнт пропорційності у разі відсутності нагартування.

Щоб зробити коефіцієнт k незалежним від розмірів пресовки, dh в рівнянні (123) необхідно розділити на її первинну висоту h₀. Проте в практичному відношенні деформацію dh зручніше відносити до приведеної висоти h_k, тобто до висоти пресовки при її 100%–й щільності.

Враховуючи викладене, а також відповідно до прийнятих допущень замість сумарного тиску P беремо тиск р на одиницю номінального поперечного перетину пресовки, рівняння (2.102) можна записати так:

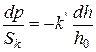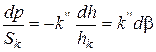, або , (2.103)

де 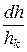, яке можна замінити на 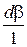, оскільки при постійному перетині пресовки об'єм змінюється так само, як і її висота;

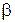– відносний об'єм пресовки.

Можна записати вираз для :

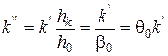, (2.104)

де 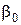– відносний об'єм насипання порошку;

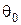– відносна щільність порошку до пресування.

Якщо врахувати, що при ущільненні деформується не весь об'єм, а тільки об'єм, які займають пори, то деформацію можна відносити не до початкового і кінцевого об'єму (висоти), а до початкового об'єму пор. В цьому випадку рівняння (2.103) можна переписати

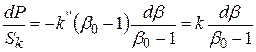, (2.105)

де 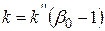– модуль пресування.

Рівняння (2.103) незручне тим, що в нього входить контактний перетин

,

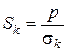де 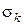– критична напруга (напруга, при якій починається пластична деформація матеріалу).

Рівняння (2.105) можна записати так: ,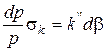

або 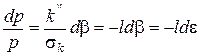, (2.106)

де 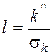– чинник пресування;

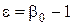– коефіцієнт пористості, який показує відношення об'єму пор до всього об'єму сипкого тіла (от 0 до ).

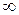Величина 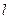пов'язана з модулем пресування 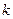таким чином:

,

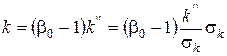або, враховуючи, що , .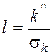

Чинник пресування 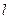у разі відсутності нагартування – величина постійна, не залежна від тиску, мало залежна від властивостей порошку і найбільш залежна від об'ємних характеристик порошку:

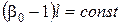. (2.107)

Слід зазначити, що насправді нагартування має дуже велике значення, величини 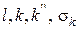помітно залежать від тиску і вираз (2.107) не зовсім точно передає дійсну залежність.

Інтегруючи рівняння (2.106):

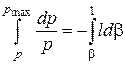, (2.108)

одержуємо ,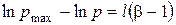

або, переходячи до десяткових логарифмів і враховуючи, що 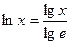, одержуємо: ,

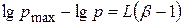або 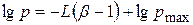(2.109)

де 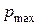– тиск, відповідний максимальному ступеню ущільнення, коли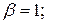

.

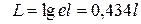Рівняння (2.109) в координатах 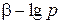, яке називають перршим рівнянням М.Ю. Бальшина, може бути графічно представлене прямою лінією (рис. 28, 1), яка характеризується двома параметрами: 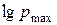– перетин прямої з віссю ординат; 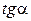– рівний чиннику пресування L.

Значення 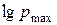для випадку нетто тиску, тобто за відсутності втрат тиску на тертя, дуже легко визначити. При максимальному ступені ущільнення площа контактного перетину рівна всій площі поперечного перетину, в даному випадку одиниці (оскільки тиску 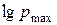відповідає перетин, рівний одиниці). При цьому 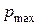, потрібне для доведення пресування до 100% густини 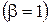, повинне дорівнювати критичній напрузі 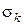, тобто

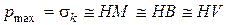
де 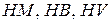– твердість відповідно по Мейеру, Бринелю, Віккерсу ( 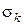більше на 5–20% ніж ).

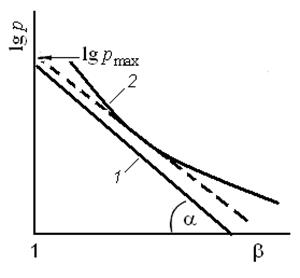
Рисунок 28 – Ідеалізована (1) і реальна (2) діаграми пресування по М. Ю. Бальшину

Іншими словами, критична напруга, при якій починається пластична деформація матеріалу частинок порошку в зоні контакту або руйнування контактних зв'язків (крихка деформація розглядається як випадок пластичної деформації), – величина постійна.

Як вже наголошувалося, чинник пресування за відсутності зміцнення матеріалу - також величина постійна. Насправді це не зовсім так.

Як видно з реальної діаграми пресування (рис.28, 2), 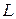– величина непостійна, і визначається в кожній точці кривої тангенсом кута дотичної до цієї крапки з віссю абсцис. Непостійність 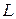можна пояснити наступним. Чинник пресування 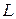, як випливає з висловленого раніше, пов'язаний з критичною напругою:

,

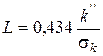де 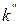– приведений модуль пресування, до певної міри аналогічний модулю Юнга (по Бальшину).

Встановлено, що 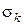не залишається постійним, а підвищується унаслідок зміцнення металу в процесі пресування.

Для деяких матеріалів в певному інтервалі тиску цією зміною можна нехтувати, а в інших випадках зміни 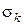і 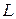настільки великі навіть в невеликих інтервалах зміни тиску пресування, що в практичних цілях рівняння (130) використати неможливо.

Бальшин відзначає, що спроби дати рівняння пресування з постійним коефіцієнтом 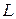для всіх порошків і у всіх інтервалах тиску приречені на невдачу.

Проте для більшості металів середньої твердості (наприклад, мідь, залізо) чинник пресування 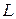може бути з достатньою для практики точністю виражений в диференціальному рівнянні:

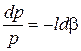
у вигляді наступної функції:

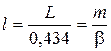, (2.110)

де 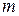– показник пресування, приблизно постійний в значному інтервалі тиску.

Підставивши вираз (2.110) в рівняння (2.108), одержимо:

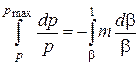. (2.111)

Інтегруючи це рівняння, одержуємо:

;

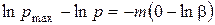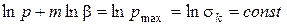(2.112)

або після потенціювання одержуємо друге рівняння Бальшина:

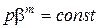(2.113)

Рівняння (2.113) можна представити так:

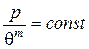. (2.114)

якщо врахувати, що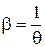

Логарифмуючи рівняння (2.113) і (2.114, одержуємо одержуємо друге рівняння М.Ю. Бальшина:

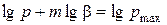, (2.115)

або 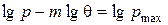(2.116)

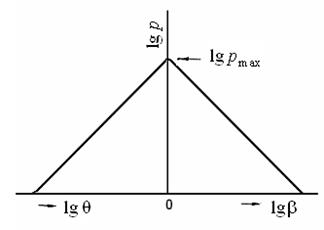Рисунок 29 – Графічний вид рівнянь (136) і (137)

Рівняння (2.115) і (2116) в графічному вигляді мають вид прямих, показаних на рисунку 29.

Тангенс кута нахилу прямих до осі абсцис визначає показник 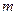, а відрізок, прямий, що відсікається, від осі ординат, рівний логарифму максимального питомого тиску пресування (у ідеальному випадку за відсутності втрат на тертя в прес-формі ).

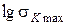На практиці діаграми 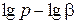в деяких випадках відрізняються від прямолінійності (рис. 30).

Якщо крива має вигин опуклості вниз ( 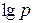зростає швидше), то в процесі пресування 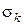не залишається постійним, а росте із збільшенням тиску пресування.

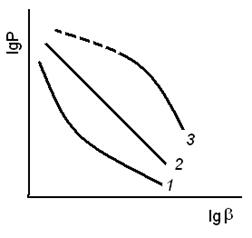Рисунок 30 – Реальні діаграми пресування

Слід мати на увазі, що вказане явище спостерігається не тільки унаслідок підвищення твердості контактних ділянок за рахунок зміцнення (по Бальшину), але і ще з двох причин:

1) унаслідок збільшення ефекту тертя між частинками, який гальмує деформацію частинок при їх взаємному стисненні (у зв'язку із збільшенням розмірів контактних ділянок);

2) унаслідок посилення об'ємних напружень, що накопичуються в частинках у міру їх деформації.

У разі, коли крива 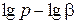має опуклість вгору (сповільнюється в зростанні 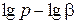), зовнішні шари частинок виявляються твердішими (через окиснення, зміцнення або яких-небудь інших причин).

Властивості частинок (форма, розмір, насипна щільність ) не впливають на 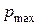. Останнє завжди, рівно тиску витікання і залежить від хімічного складу порошку.

При отриманні пресовок з щільність менше 100% властивості порошків сильно впливають на тиск пресування, необхідний для досягнення певної щільності пресовок з причин, розглянутих раніше.

На закінчення можна сказати, що, на думку Ждановича, логарифмічні і напівлогарифмічні рівняння пресування Бальшина, виведені з фізичних передумов, лише приблизно відображають суть процесу в цілому, маючи достатню точність при постійних значеннях коефіцієнтів і показників тільки в обмеженому діапазоні тиску.