Пресування за О.П.Реутом, Л.С.Богінським, Е.Е.Петюшиком

Теоретичні розрахунки на міцність, технологические процессы передбачають обов’язковим присутність в рівняннях стану емпіричних констант. При цьому наявність таких трьох констант матеріалу задовольняє як задовільну точність розрахунків, так і можливість подальшого теоретичного аналізу процесів з врахуванням структури та особливостей матеріалу.

З математичної точки зору якщо теоретична модель матеріалу вміщує в собі вплив на досягнення пластичної течії першого і другого інваріантів напружень І₁ і І₂, використання трьох емпіричних констант дозволяє інтерпретувати критерій пластичності у просторі головних напружень у вигляді поверхні другого ступеня:

(2.146)

Ця поверхня симетрична до напрямів трьох головних напружень.

Замкнута поверхня навантаження порошкових матеріалів у напрямі гідростатичної вісі стискання може мати вигляд

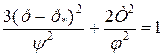. (2.147)

де 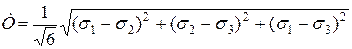– інтенсивність дотичних напружень;

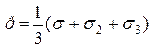– гідростатичний тиск;

– параметр зміщення центру еліпсоїду впродовж гідростатичної вісі, який враховує різницю в опорі пресовок розтягуванню та стисненню;

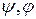– функції механічних характеристик матеріалу, що ущільнюється.

Для другої поверхні (рис. 35) навантаження у вигляді зсунутого еліпсоїду обертання рівняння поверхні має вигляд:

Рисунок 35 – Вигляд поверхні навантаження згідно рівняння (2.147)

Для випадку пресування порошкових матеріалів явний вигляд поверхні еліпсоїду навантаження по розрахунковим або емпіричним оцінкам опору деформації порошкових пресовок різної щільності буде залежати від схеми навантаження.

Так для гідростатичного стиснення, коли 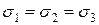і Т=0 з рівняння (2.147) отримуємо:

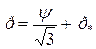(2.148)

Якщо рахувати, що опір порошку гідростатичному стисканню описується рівнянням Г. М. Жданович, яке враховує властивості порошку та його зміцнення у вигляді:

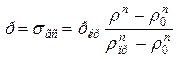, (2.149)

де р_кр – критична (максимальна) гідростатична напруга стискання, яка необхідна для отримання максимальної щільності пресовки (густини компактного матеріалу) , коли ;

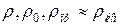– щільність пресовки, насипна щільність порошкового матеріалу та щільність компактного матеріалу відповідно;

n – показник інтенсивності зміцнення порошкового матеріалу в умовах гідростатичного стиснення;

– опір порошкових матеріалів гідростатичному стисненню.

Прирівнюючи рівняння (2.147) та (2.148), отримуємо

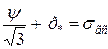. (2.150)

При вільній осадці , а 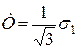. При цьому рівняння (2.148) для випадку пресування вільною осадкою можна представити у вигляді

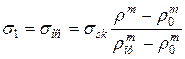, (2.151)

де – опір деформації порошкової пре совки при щільності ;

m – казник , який характеризує інтенсивність збільшення опору деформації порошкового матеріалу зі збільшенням його щільності в умовах вільної осадки;

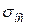– опір деформуванню порошкових матеріалів при вільній осадці.

Враховуючи це , рівняння (2.146) перетворюється у вигляд:

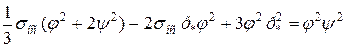(2.152)

У випадку осьового пресування у закритій пресформі без врахування сил зовнішнього тертяприймаємо

,

де 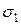– напруження пресування (тиск пресування); – опір деформуванню порошкових матеріалів при осьовому пресуванні в закритих пресформах без врахування сил зовнішнього тертя.

Тоді :

,

де 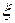– коефіцієнт бокового тиску, який залежить від щільності пресовки та властивостей порошку, .

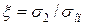У цьому випадку:

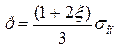а 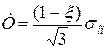. (2.153)

Для визначення можна використати також рівняння Г.М.Ждановича , яке для випадку осьового пресування в закритих пресформах без врахування сил зовнішнього тертя можна представити у вигляді:

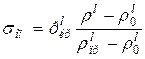, (2.154)

де 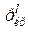– критичні (межеві) напруження, які необхідні для отримання максимальної щільності ( ) при пресуванні в закритій пресформі без врахування сил зовнішнього тертя;

l – показник зміцнення.

Тоді рівняння (2.147) приймає вигляд:

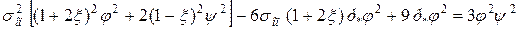(2.155)

Для визначення 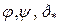по відомим виразам для та 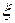необхідно вирішити систему рівнянь (2.150), (2.151), (2.2.155).

Визначимо 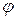з рівняння (2.152). Маємо :

(2.156)

З врахуванням рівняння (2.155) отримаємо:

(2.157)

Прирівнюючи праві частини (2.156) та (2.157) та враховуючи, що

, визначимо .

Тоді отримаємо :

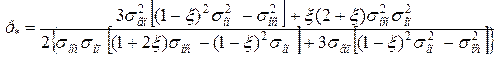. (2.158)

Враховуючи те, що з (2.3) 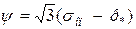, підставляючи цей вираз в (2.156), маємо:

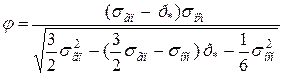. (2.159)

Таким чином, умова пластичності (2.147) для випадку осьового пресування в закритих матрицях буде мати вигляд:

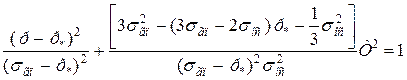(2.160)

Для визначення опорів деформації при вибраних схемах навантаження можна також скористатись іншими рівняннями пресування, наприклад рівняннями М. Ю. Бальшина або Н. Ф. Куніна і Б. Д. Юрченка . Важливо тільки, щоб вони максимально точно описували процес ущільнення порошку з врахуванням зміни щільності та структури матеріалу. Це можуть бути рівняння запропоновані М.Ю. Бальшиним і С.С. Кіпарісовим та Г.М.Ждановичом, які отримані виходячи з контактної теорії пресування.

Спільний розгляд традиційних поглядів про процеси ущільнення порошкових матеріалів з континуальним підходом дозволить отримати найбільш повну картину поведінки порошкових тіл при деформації.

Рисунок 36 – Слід поверхні навантаження в р-Т площині

На рисунку 36 показано слід поверхні навантаження в координатах Р і Т. Модель пластичності (2.15) враховує ефект різниці межі текучості при розтягуванні та стисканні. Рівняння, які входять до неї (2.4), (2.6), (2.7) (2.9) і визначають математичне формулювання , вміщують параметри, що враховують зміцнення та структуру порошкового тіла. Відомо, що коефіцієнт бокового тиску, який визначається при осьовому пресуванні в матриці, залежить від коефіцієнту міжчастинкового тертя і, тим самим, від матеріалу порошку, розміру та форми частинок, щільності. Таким чином можна комплексно врахувати структурні зміни у процесі пресування.

Модель пластичності (2.160) порошкового тіла, що ущільнюється, у вигляді зсунутого еліпсоїду обертання є багатопараметричною. Вона визначає зв’язок компонент тензора напружень з щільністю, структурними характеристиками пресовки і може бути основою для розрахунків основних схем ущільнення порошку.