Принципом возможных перемещений

Силовой расчет и динамическое исследование механизма можно всегда произвести, если использовать принцип возможных перемещений.

Принцип возможных перемещений гласит: если на какую либо механическую систему действуют силы, то, прибавляя к заданным силам силы инерции и давая ей возможные перемещения, получаем ряд элементарных работ, сумма которых должна равняться нулю. Т.е.:

В=S P

α

DS

б)

М

φ

Рисунок 3.12, а-б

между вектором действия силы и проекцией элементарного перемещения; М-момент, действующий на систему; Dφ - элементарный угол, на который поворачивается система.

Чтобы система находилась в равновесии, на механизм должна действовать уравновешивающая сила Р_ур. Элементарная работа под действием этой силы вычисляется по формуле (3.28). Подставляя формулы (3.28) и (3.29) в уравнение (3.27) и учитывая уравновешивающую силу, имеем:

SDA_ί = SР_ίDS_ίcosα_ί + SМ_ίDφ_ί - Р_ур DS_урcosα_ур = 0. (3.30)

Т.к. механизм является кинематической цепью принужденного движения не зависящего от времени, то возможные перемещения можно принять за действительные. Т.е.:

SdA_ί =SР_ίdS_ίcosα_ί + SМ_ίdφ_ί - Р_урdS_урcosα_ур = 0. (3.31)

Но, разделив обе части уравнения на dt и учитывая, что dS/dt = υ, dφ/dt = ω, получим:

SР_ίυ_ίcosα_ί + SМ_ίω _ί - Р_урυ _урcosα_ур = 0. (3.32)

Отсюда выразим уравновешивающую силу Р_ур

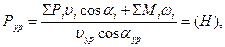(3.33)

где Р_ί - сила i-того звена, υ_ί - скорость точки, к которой приложена уравновешивающая сила, α_ί - угол, образованный между линией действия силы и вектором скорости; М_ί - момент i-того звена; ω_ί - угловая скорость i-того звена.

Т.к. угол α_ур = 0^о (рис. 3.10), cosα_ур = 1 и скорость приложена к т. А, тогда формула (3.33) примет вид

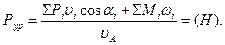(3.34)

Применим этот метод на конкретном примере.