Кинетостатический (силовой) расчет шестизвенного

механизма (пример выполнения)

Исходные данные для расчета: ℓ_ОА, ℓ_АВ, ℓ_ВС - длины звеньев в м; ℓ_ОС-межосевое расстояние в м; ℓ_У - расстояние до хода ползуна 5 в м; ℓ_О1_S1, ℓ_А_S2, ℓ_С_S3 - расстояния до центров масс в м; m₁, m₂, m₃, m₅ - массы звеньев в кг; φ - угол положения кривошипа.

Определить: Скорости и ускорения всех точек звеньев механизма; R₆₁, R₂₁, R₂₃, R₆₃, R₆₅– реакции в кинематических парах; Р_ур- уравновешивающую силу.

Решение.

1. Изображение механизма в масштабе μ_ℓ. Высчитываем масштабный коэффициент по формуле (2.1): μ_ℓ= ℓ_О1А/ОА = (м/мм). Затем считаем чертежные значения межосевого расстояния ОС = ℓ_ОС/μ_ℓ, расстояния y = ℓ_y/μ_ℓ и длин звеньев АВ = ℓ_АВ/μ_ℓ, ВС = ℓ_ВС/μ_ℓ в мм. Откладываем межосевое расстояние ОС и под углом φ проводим длиной ОА положение кривошипа. После этого из точки А проводим дугу, равную радиусу R₁=[АВ], а из точки С проводим дугу, равную радиусу R₂ = [ВС]. На пересечении этих двух дуг получаем точку В. Далее проводим горизонтальную линию на расстоянии у и отмечаем точку D. Изображаем опоры и кулисный камень (рисунок 3.14, а).

2. Кинематическое исследование механизма (определение скоростей и ускорений всех точек звеньев механизма методом планов).

Кинематический анализ механизма начинается с 1-го (ведущего) звена, т.к. известны его положение и длина. Высчитываем скорость точки А по формуле (2.26)

υ_А= ω₁ℓ_ОА=(м/с),

а затем масштабный коэффициент плана скоростей по формуле (2.30)

μ_υ= υ_А/[Р_υа] = ( ).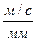

К механизму I класса присоединяется структурная группа 2-3. Она является группой II класса 1 вида. Методика построения плана скоростей и ускорений этой группы рассмотрена в п. 2.4.2, Задача 1. Остановимся кратко. Скорости внешних шарниров А и С известны: υ_А рассчитана выше, а υ_С = 0. Для определения скорости точки В запишем векторные уравнения:

υ_В= υ_А+ υ_ВА ^ АВ

υ_В= υ_С+ υ_ВС ^ ВС.

Начинаем построение плана скоростей. Из произвольно выбранной точки полюса Р_υ проводим вектор скорости υ_А^ ОА в сторону угловой скорости ω₁ длиной [Р_υа]. Затем из точки а проводим линию, перпендикулярную звену АВ, а из точки Р_υ – линию, перпендикулярную звену ВС. На пересечении получаем точку в. Вектора направляем к ней (рисунок 3.14, б). Рассмотрим группу 4-5. Она является группой II класса 4 вида. Методика рассмотрена в п. 2.4.2, Задача 4. В точке D соединяется 4 звена. Поэтому будет четыре точки – D₃, D₄, D₅, D₆. Скорость υ_D3 найдем по правилу подобия, т.к. эта точка расположена на продолжении звена ВС. Составим пропорцию по уравнению (2.43)

ℓ_ВС/ℓ_С_D3= [вс]/[Р_υd₃].

Выразив отрезок [Р_υd₃] в мм, отложим его на продолжении вектора Р_υd₃, так, чтобы порядок букв соответствовал порядку букв на схеме механизма. Далее находим точку D₄, скорость которой равна скорости точки D₅ (υ_D4= υ_D5). Для этого составляем векторные уравнения:

υ_D₄= υ_D₃+ υ_D₄_D₃ êêВD

υ_D5= υ_D6+ υ_D5_D6 êêх-х.

Из точки d₃ проводим линию, параллельную ВD, а из полюса (т.к. υ_D6= 0) проводим линию, параллельную горизонтальной линии х-х. На пересечении получаем точку d₄=d₅. Вектора также направляем к найденной точке (рисунок 3.14, б). После построения плана скоростей, высчитываем все действительные значения линейных и угловых скоростей, а также определяем их направления:

υ_В= υ_ВC= [Р_υв] μ_υ=

υ_D₅= [Р_υd₅] μ_υ= (м/с);

υ_ВА = [ав] μ_υ=

υ_D3_D4= [d₃d₄] μ_υ =

ω₂= υ²_ВА/ℓ_АВ =

ω₃= ω₄= υ²_ВС/ℓ_ВС = (с^-1).

Для определения направления угловых скоростей, нужно векторы относительных скоростей перенести в точку В и мысленно поворачивать звенья АВ и ВС относительно точек А и С. Направление ω₂ получилось против часовой стрелки, а ω₃ – по часовой стрелке (рисунок 3.14, а).

Начинаем построение плана ускорений. Считаем ускорение точки а_А

а_А=аⁿ_АО=ω₁²ℓ_ОА =(м/с²).

Затем высчитываем масштабный коэффициент плана ускорений:

μ_а= а_А/[Р_аа] =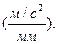

Запишем векторные уравнения ускорений для точки В:

а_В= а_А+ аⁿ_ВАêêАВ + а^τ_ВА^АВ

а_В= а_С+ аⁿ_ВСêêВС + а^τ_ВС^ВС.

Считаем нормальные ускорения в м/с² по формулам (2.38)

аⁿ_ВА= υ²_ВА/ℓ_АВ

аⁿ_ВС= υ²_ВС/ℓ_ВС,

а затем вектора нормальных ускорений в мм:

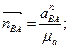
Из произвольно выбранной точки полюса Р_а откладываем вектор ускорения точки А параллельно ОА к центру вращения (к точке О) длиной [Р_аа]. Затем из точки а проводим вектор нормального ускорения аⁿ_ВА параллельно звену АВ к точке А длиной 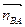. Через конец вектора 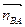проводим линию действия тангенциального ускорения а^τ_ВА перпендикулярно звену АВ. После этого из полюса Р_а откладываем вектор нормального ускорения аⁿ_ВС параллельно звену ВС в сторону к точке С длиной 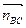. Через конец вектора 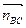проводим линию действия тангенциального ускорения а^τ_ВС перпендикулярно звену ВС. На пересечении этих линий действия получаем точку в (рисунок 3.14, в). Точку d₃ находим по правилу подобия:

ℓ_ВС/ℓ_С_D3 = [вс]/[Р_аd₃].

Отрезок [Р_аd₃] откладываем на продолжении вектора [Р_ав]. Для нахождения скорости точки D₄,₅ составим векторные уравнения

а_D₄= а_D₃+ а^K_D₄_D₃+ а^r_D₄_D₃ || ВD

а_D5= а_D6+ а^к_D5_D6+ а^r_D5_D6 || х-х.

Высчитываем кориолисово ускорения по формулам

а^к_D4_D3=2ω₄υ_D4_D3; а^к_D5_D6= 0,

а затем чертежные значения

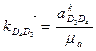= (мм).

Из точки d₃ проводим вектор кориолисова ускорения перпендикулярно звену ВС длиной 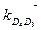, повернув вектор относительной скорости υ_D4_D3 на 90^о в сторону ω₄. Через конец вектора 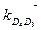проводим линию действия релятивного (относительного) ускорения а^r_D4_D3 параллельно звену ВD. Затем из полюса откладываем линию действия относительного ускорения а^r_D5_D6 параллельно горизонтальной оси х-х. На пересечении этих линий действия получаем точку d_4,5. Высчитываем действительные значения всех ускорений:

а_В= [Р_ав]μ_а = (м/с²);

а_D5= [Р_аd₅]μ_а = (м/с²);

а^τ_ВА= [n_ВАв]μ_а = (м/с²);

а^τ_ВС= [n_ВСв]μ_а= (м/с²);

ξ₂= а^τ_ВА/ℓ_АВ = (с^-2);

ξ₃ = а^τ_ВС/ℓ_ВС = (с^-2).

Для определения направления угловых ускорений, нужно вектора тангенциальных ускорений мысленно перенести в точку В на схеме механизма и вращать звено АВ относительно точки А, звено ВС относительно точки С. Получается, что ξ₂и ξ₃направлены по часовой стрелке (рисунок 3.14, а).

Определим ускорения центров масс. Сначала отметим точки S₁, S₂, S₃, S₅ на схеме механизма. Для этого вычислим расстояния: ОS₁= ℓ_OS1/μ_ℓ, AS₂ = ℓ_AS1/μ_ℓ, CS₃= ℓ_CS3/μ_ℓ, S₅= D₅. Эти же точки найдем на плане ускорений по правилу подобия, используя соотношение отрезков

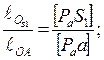
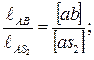
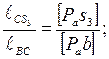
т. s₅= т. d₅.

Выражаем из этих пропорций отрезки [Р_аS₁], [aS₂], [Р_аS₃] и откладываем их на соответствующих векторах плана ускорений (рисунок 3.14, в). Соединяем эти точки с полюсом Р_а и высчитываем ускорения центров масс:

a_S₁= [Р_аS₁] μ_а = (м/с²);

a_S₂= [Р_аS₂] μ_а= (м/с²);

a_S₃ = [Р_аS₃] μ_а = (м/с²); (3.40)

a_S₅= а_D5=[Р_аd₅]μ_а = (м/с²).

После расчетов всех скоростей и ускорений приступаем к выполнению силового расчета, т.е. к нахождению реакций и силы Р_ур.

а) Схема механизма μ_ℓ = б) План скоростей μ_υ=

B 2 A υ_D5D3 d₃ υ_D3 P_υ υ_A a

ξ₃ ω₂ d₅υ_BA

3 ω₃ ξ₂ 1 ω₁ υ_D5 υ_В в

C O

6 в) План ускорений μ_а=.

D у 6 k d₃

4 6 P_a

5 d₅, S₅ S₃

n_ВС

г) Структурная группа 4-5 и ее план сил в

R₃₄ μ_Р₁=… S₁ S₂

P_и₅ R₆₅ P_P R₃₄

D a n_ВА

G₅ R₆₅

G₅ P_и₅

μ_Р2=…

д) Структурная группа 2-3 и ее план сил Rⁿ₁₂

P^´_и2 P^´_и3 P_P

h₃R₆₃ R₁₂

М_РИ₂ G₃ R^t₁₂

h₄ B S₂ T₂ A Rⁿ₆₃

P^´_и₃ Rⁿ₁₂ R₄₃ G₂

М_Ри₃ S₃K₃ R₆₃ G₂ R^t₁₂ R₁₂ R^t₆₃P^´_и₂

R^t₆₃ C ж) Рычаг Жуковского μ_υ=…

h₂ h₁ P_и₅

Rⁿ₆₃ G₃ d₅ d₃

G₅

R₄₃

P_υ h₁

е) Механизм I класса и его план сил Р_и3 h₅

R₂₁ μ_Р₃=… P_P Р_и₁

P_и₁ R₆₁ Р^´_и₃ s₃ s₁

A h₂ k₃ G₁

P_ур s₁R₆₁ G₁ G₃ Р^´_и₂

O R₂₁ в s₂ t₂ a

G₂ h₄

h₁ P_и₁ P_ур h₃h₂

G₁

Рисунок 3.14 - Пример силового расчета шестизвенного механизма

3. Силовой (кинетостатический) расчет шестизвенного механизма.

Определяем силы тяжести: G₁= m₁g = (H), G₂= m₂g = (H),

G₃= m₃g = (H), G₅= m₅g = (H).

Определяем силы инерции: Р_и1= -m₁a_S₁ = (Н), Р_и2= -m₂a_S₂ = (Н),

Р_и3= -m₃a_S₃ = (Н), Р_и5= -m₅a_S₅ = (Н).

Определяем моменты от сил инерции: М_Ри2= -ξ₂J_S2 = (Нм),

М_Ри3= -ξ₃J_S3 = (Нм), М_Ри1= М_Ри4= М_Ри5 = 0.

Определяем направление моментов. Момент от силы инерции направлен в противоположную сторону угловому ускорению. Т.е.: М_Ри2 и М_Ри3 направлены против часовой стрелке (рисунок 3.14, а).

Определяем реакции в кинематических парах. Для этого выполняем структурный анализ (глава 1, §1.7). В данном механизме имеется одна структурная группа II класса 1 вида и одна структурная группа II класса 4 вида. Как указывалось в п. 3.1.4.1, силовой расчет начинаем с последней группы, т.е. с группы 4 вида. Порядок проведения силового расчета данной структурной группы рассмотрен в п. 3.1.4.3, Задача 4. Изображаем структурную группу в том же масштабе и том же положении, что и схема механизма (рисунок 3.14, г). Прикладываем G₅ вертикально вниз и Р_и5 в обратную сторону вектору а_D5. Составляем векторное уравнение плана сил, из которого находим R₆₅ и R₃₄:

, .

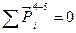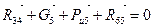Высчитываем масштабный коэффициент плана сил μ_Р1 =Р_и5/[Р_и5] =(Н/мм). Затем считаем вектор силы тяжести [G₅] = G₅/μ_Р1 = (Н). Построение начинаем согласно уравнению с вектора G₅. К концу вектора G₅ прикладываем вектор Р_и5. Направление реакций нам известны: R₆₅ направлена вертикально, R₃₄ направлена перпендикулярно звену ВD (глава 3, п. 3.1.4.1). Поэтому из начала построения проводим линию действия R₃₄ перпендикулярно ВD , а из конца Р_и5 – линию действия R₆₅ вертикально. Точка пересечения даст начало R₃₄ и конец R₆₅ (рисунок 3.14, г). Определяем действительные значения реакций

R₆₅= [R₆₅] μ_Р1 = (Н);

R₃₄ = [R₃₄] μ_Р1 = (Н).

Приступаем к силовому расчету структурной группы 1 вида (группа 2-3). Изображаем ее в том же масштабе, что и схема механизма (рисунок 3.14, д). В точке S₂ прикладываем G₂ вертикально вниз Р_и2 в обратную сторону вектору a_S₂. В точку S₃ прикладываем G₃ и Р_и3. Прикладываем направления моментов. Заменяем момент инерции и силу инерции одной силой, приложенной не в центре масс. Для шатуна имеем: h_Ри2= М_Ри2/Р_и2μ_ℓ =(мм); для кулисы - ℓ_СК3= ℓ_С_S3+(Ј_S3/m₃ℓ_С_S3) = (м). Переносим силу Р_и2 параллельно самой себе на величину h_Ри2, получаем замененную силу Р′_и2 и точку ее пересечения со звеном АВ (точку Т₂). Для нахождения точки приложения Р′_и3 необходимо от точки С в сторону к точки В отложить расстояние СК₃= ℓ_СК3/μ_ℓ = (мм) и перенести силу Р_и3 параллельно самой себе в точку К₃. По величине и направлению замененные силы будут равны действительным, т.е.:

Р′_и2= Р_И2; Р′_и3= Р_и3.

Прикладываем реакции: в точках А и С будут действовать нормальные составляющие Rⁿ₁₂ и Rⁿ₆₃, направленные параллельно звеньям, и тангенциальные составляющие R^t₁₂ и R^t₆₃, направленные перпендикулярно звеньям. В точке D будет действовать реакция R₄₃, которая равна по величине реакции R₃₄, но противоположна по направлению: R₄₃= -R₃₄.

Далее расчет ведем аналогично п. 3.1.4.3, Задача 1. Составляем уравнения моментов каждого из звеньев относительно точки В:

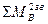= 0, R^t₁₂ АВ - Р′_и2h₃+ G₂ h₁= 0;

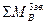= 0, R^t₆₃ СВ - Р′_и3h₄+ G₃h₂+ R₄₃CD = 0.

Из этих уравнений выражаем тангенциальные реакции. Составляем векторное уравнение плана сил:

, .

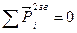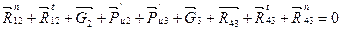Высчитываем масштабный коэффициент плана сил

μ_Р2= R^t₁₂/[R^t₁₂] = (Н/мм).

Построение векторного многоугольника начинаем с реакции R^t₁₂. Далее к концу каждого вектора прибавляем следующий согласно уравнению. Вектора сил переносим параллельно со структурной группы. Дины векторов высчитываются по формуле

[G₂] = G₂/μ_Р2= (мм), [Р′_и2] = Р′_и2/μ_Р2 = (мм) и т.д.

Затем из начала построения проводим линию действия Rⁿ₁₂ параллельно АВ, а из конца построения – линию действия Rⁿ₆₃ параллельно BD. На пересечении получаем точку, которая является началом Rⁿ₁₂ и концом Rⁿ₆₃. Соединяем начало Rⁿ₁₂ с концом R^t₁₂ – получаем вектор реакции R₁₂. Соединяем начало R^t₆₃ с концом Rⁿ₆₃ – получаем вектор R₆₃ (рисунок 3.14, д). Найдем реакцию во внутреннем шарнире R₂₃ (см. п.1.4.3, Задача 1). Составим уравнение:

, .

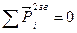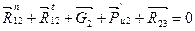Находим действительные значения полученных реакций

R₁₂= [R₁₂]μ_Р2 =

R₆₃ = [R₆₃]μ_Р2 = (Н).

R₂₃ = [R₂₃]μ_Р2 =

Приступаем к силовому исследованию ведущего звена (механизму I класса). Изображаем кривошип с опорой в том же масштабе и положении. В точку S₁ прикладываем силу тяжести G₁ вертикально вниз и силу инерции Р_и1, которая параллельна ускорению a_S₁, но направлена в противоположную сторону. К точке А прикладываем реакцию R₂₁, которая по величине равна R₁₂, но противоположна по направлению (R₂₁=-R₁₂). В точку А прикладываем и уравновешивающую силу Р_ур, которая направлена перпендикулярно звену ОА (рисунок 3.14, е). Силовой расчет проводим по 1-му методу (п. 3.1.5). Составляем уравнение моментов относительно точки О:

∑М^._О= 0, Р_урОА - R₂₁h₂+ G₁h₁= 0,

из которого выражаем уравновешивающую силу Р_ур. Составляем векторное уравнение механизма I класса:

, .

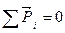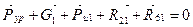План сил строим аналогично (см. п. 1.4.3). Соединяя начало вектора силы Р_ур с концом вектора R₂₁, получаем вектор реакции R₆₁ и находим действительное ее значение

R₆₁ = [R₆₁]μ_Р3 = (Н).

Итак, мы определили реакции в кинематических парах и Р_ур методом планов. Рассчитаем уравновешивающий момент

М_ур=Р_урℓ_OA=(Нм)

и мощность двигателя

N_дв= М_урω₁ = (Вт).

Теперь выполним проверку определения Р_ур методом Н.Е.Жуковского.

4. Рычаг Н.Е. Жуковского. Строим план скоростей, повернутый на 90^о в сторону вращения угловой скорости (можно в обратную) относительно точки полюса Р_υ. Точки s₁, s₂, s₃, t₂ и k₃ находим по п.2. правила подобия (п. 2.4.2):

ℓ_OS1/ℓ_OA=[Р_υs₁]/[Р_υa];

ℓ_AВ/ℓ_AS2=[aв]/[as₂];

ℓ_CS3/ℓ_BC=[Р_υs₃]/[Р_υв];

ℓ_AВ/ℓ_AТ2=[aв]/[at₂];

ℓ_CК3/ℓ_BC=[Р_υk₃]/[Р_υв].

Определяем отрезки [Р_υs₁], [as₂], [Р_υs₃], [at₂], [Р_аk₃] в мм и отмечаем их на соответствующих векторах. Со структурных групп и с механизма I класса параллельно переносим все силы. Силы тяжести G₁, G₂, G₃ прикладываем в точки s₁, s₂, s₃; силу инерции Р′_и2 прикладываем в точку t₂; Р′_и3 – в точку k₃; Р_и1 – в точку s₁; G₅ и Р_и5 – в точку d₅; Р′_ур – в точку a. Реакции не прикладываются! Составляем сумму моментов относительно полюса Р_υ:

SМ_Рυ= 0, Р′_ур[Р_υa]+G₁h₁-G₂h₂-G₃h₃+ Р′_и2h₄+ Р′_и3h₅+ Р_и5[Р_υd₅] = 0

и выражаем Р′_ур. Рассчитаем процент ошибки между двумя методами. Расхождение не должно составлять более 5%:

Δ=(Р_ур- Р´_ур)/ Р_ур≤5%.

Определяем мощность двигателя

N_дв = Р_ур υ_А.= (Вт).

На этом силовой расчет шестизвенного механизма считается законченным.

<24 25 262728 29 30 >

Дата добавления: 2015-10-19; просмотров: 1061;