Система счисления

Для записи чисел в конкретной системе счисления используется некоторый конечный алфавит, состоящий из цифр a₁ а₂ а₃ ... а_n, которые называются базисными числами. В современном мире наиболее распространенными являются представление чисел посредством арабских цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. В римской системе счисления базисными являются числа 1, 5, 10, 50, 100, 500, 1000, которые обозначаются I, V, X, L, C, D, M, а другие получаются путем сложения и вычитания базисных. Напр. 146 – CXLVI (C- 100, XL-40, VI-6). Римская система счисления является непозиционной. Непозиционные системы в ЭВМ не применяются.

Существуют позиционные и непозиционные системы счисления.

В непозиционных системах счисления вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позициив записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.

Сама же запись числа 757,7 означает сокращенную запись выражения:

700 + 50 + 7 + 0,7 = 7+10² + 5*10 + 7*10⁰ + 7*10^-1= 757,7.

Любая позиционная система счисления характеризуется своим основанием.

За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения:

a_n-1 q^n-1 + a_n-2 q^n-2 + ... + a₁ q¹ + a₀ q⁰ + a_-1 q^-1 + ... + a_-m q^-m,

где a_i —цифры системы счисления; n и m — число целых и дробных разрядов, соответственно, q- основание системы.
Например:

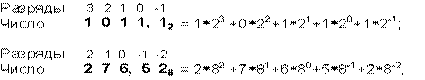
§ Самая маленькая система счисления – это двоичная, имеющая только две цифры: 0, 1.

§ в троичной системе: 0, 1, 2.

§ в пятеричной системе: 0, 1, 2, 3, 4.

§ в восьмеричной системе: 0, 1, 2, 3, 4, 5, 6, 7.

В компьютере используются следующие системы счисления:

· двоичная (используются цифры 0, 1);

· восьмеричная (используются цифры 0, 1, ..., 7);

· шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1, ..., 9, а для следующих чисел — от десяти до пятнадцати — в качестве цифр используются символы A, B, C, D, E, F).

Таблица соответствия систем счисления:

Двоичная система счисления получила самое широкое распространение в ЭВМ благодаря тому, что очень проста в применении с точки зрения технической реализации процесса представления чисел в ЭВМ. Т.е. для физического представления чисел необходимы элементы, которые могут находиться в одном из двух устойчивых состояниях: выключатель включен(этому состоянию логически соответствует 1) и выключатель выключен (0).