Перевод из 10-ой системы счисления в q-ую (2, 8, 16-ую систему счисл.)
Перевод целой и дробной частей числа производится раздельно по определенным алгоритмам. Для целой части этот метод называется методом последовательного деления на основание системы счисления, а для дробной части методом последовательного умноженияна основание системы.
а) для целой части числа:
Число А многократно делим на основание системы счисления р (2, 8 или 16) до тех пор, пока частное от деления не станет меньше делителя. При этом первый остаток будет младшим разрядом, а последнее частное является старшим разрядом. Все остатки записываются по порядку «справа-налево».
Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
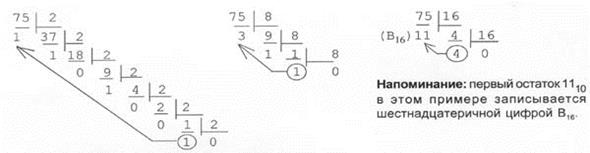
Ответ: 7510 = 1 001 0112 = 1138 = 4B16.
b) для дробной части числа:
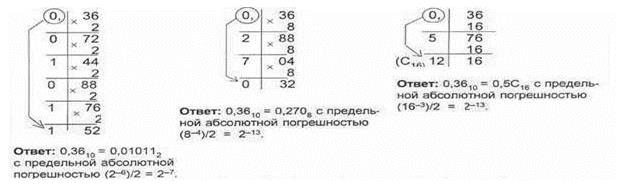
Число А многократно умножается на основание системы счисления q (2, 8 или 16) до тех пор, пока не будет получен 0 в дробной части, либо до определенного количества значащих цифр. Разряды записываются «сверху-вниз».
Пример. Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
4.2.2 Перевод из q-ой системы счисления (2, 8, 16-ой) в 10-ую:
| Перевод в десятичную систему числа x, записанного в q-ичной cистеме счисления (q = 2, 8 или 16) сводится к вычислению значения многочлена x10 = an qn+ an-1 qn-1 + ... + a0q0 + a-1 q-1 + a-2 q-2 + ... + a-m q-m средствами десятичной арифметики. |
Примеры:

4.2.3 Перевод из 2-ой системы в 8, 16-ую систему счисления и наоборот:
| Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой. |
Например,

Старшая группа разрядов исходного числа при необходимости дополняется слева нулями до триады (тетрады).
| Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр). |
Например:

Дата добавления: 2015-10-19; просмотров: 1417;
