Логические операции и таблицы истинности

Например, составное высказывание F=«2*2=4 или 3*3=10» истинно (F=1), поскольку первое простое высказывание истинно (А=1), а второе – ложно (В=0).

3. Инверсия (логическое отрицание, частица не(not))делает истинное высказывание ложным и, наоборот, ложное - истинным.

Запись:

Пример. "Луна — спутник Земли" (А); "Луна — не спутник Земли" ( ).

4. Операция XOR – исключающее ИЛИ (сложение по модулю 2, отрицание равнозначности)

Обозначается оборотом речи «либо…, либо…» Составное утверждение «либо A, либо B» считается истинным, когда истинно либо A, либо B, но не оба сразу; в противном случае составное утверждение ложно.

Т.е. результат истинен (равен 1), если A не равно B (A≠B).

Эту операцию нередко сравнивают с дизъюнкцией потому, что они очень похожи по свойствам, и обе имеют сходство с союзом «или» в повседневной речи. Сравните правила для этих операций:

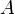1. истинно, если истинно или 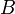, или оба сразу.

2. 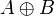истинно, если истинно 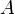или 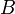, но не оба сразу.

Операция исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ». Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.

5. Импликация (логическое следование)образуется соединением двух высказываний в одно с помощью оборота речи «если …, то ….».

Запись: А®В

Составное высказывание, образованное с помощью операции импликации, ложно тогда и только тогда, когда из истинной предпосылки (первого высказывания) следует ложный вывод (второе высказывание).

Т.е. если из 1 следует 0, то результат – 0, в остальных случаях – 1.

Например, высказывание «Если число делится на 10, то оно делится на 5» истинно, т.к. истинны и первое и второе высказывание.

Высказывание «Если число делится на 10, то оно делится на 3» ложно, т.к. из истинной предпосылки делается ложный вывод.

"Данный четырёхугольник — квадрат" (А) и "Около данного четырёхугольника можно описать окружность" (В). Тогда составное высказывание , читается как "Если данный четырёхугольник квадрат, то около него можно описать окружность".

В обычной речи связка "если ..., то" описывает причинно-следственную связь между высказываниями. Но в логических операциях смысл высказываний не учитывается. Рассматривается только их истинность или ложность. Поэтому не надо смущаться "бессмысленностью" импликаций, образованных высказываниями, совершенно не связанными по содержанию. Например, такими: "если президент США — демократ, то в Африке водятся жирафы", "если арбуз — ягода, то в бензоколонке есть бензин".

6. Эквивалентность (логическое равенство, ~ º Û) образуется соединением двух высказываний в одно с помощью оборота речи « …тогда и только тогда, когда ...»

Составное высказывание, образованное операцией эквивалентности, истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.

Например, высказывание «Компьютер может производить вычисления тогда и только тогда, когда он включен» и «Компьютер не может производить вычисления тогда и только тогда, когда он не включен» - истинны, поскольку оба простых высказывания одновременно истинны.