Кирхгоф заңдары және олардың тізбектерді есептеуде қолданылуы

Электр тізбектеріндегі негізгі заңдылық Кирхгоф заңдары болып есептеледі. Олай болу себебі - тізбектерге жүргізілген қандай да талдау немесе есептеулер болмасын олардың барлығы Кирхгоф заңдарына сүйенеді. Сондықтан тізбектерді есептеудің түрлі тәсілдерін қарап жатпай, Кирхгоф заңдарын тікелей қолдануды қарастырса жеткілікті.

Г.Р.Кирхгоф (1824-1887) неміс физигі, аталмыш заңдарды 1847 жылы тапқан.

Тізбектерді есептеу деп олардың белгісіз параметрлері мен электрлік шамаларын табуды айтады. Әдетте ЭҚК не толық кернеу және кедергілер белгілі де, оларды пайдаланып тізбек элементтерінің токтарын, кернеулерін және қуаттарын анықтау керек болады.

Қарастырып отырған тізбекте (3-сурет) ЭҚК-тің және кедергілердің сан мәндері белгілі екен делік. Тізбекті құрастырғаннан және ЭҚК көзіне қосқан кейін тармақтармен ток жүре бастайды. Электр тогын зарядтардың (ұйықтардың) бір бағыттағы тәртіптелген қозғалысы деп түсінсек қанша заряд түйінге келіп жетсе, сонша заряд түйіннен кетіп отырады: түйінге келіп жеткен зарядтар онда тоқталып немесе жиналып қалмайды. Міне осы факт Кирхгофтың бірінші заңы болып есептеледі. Оны математика тілінде былай жазуға болады:

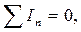(1)

яғни түйінде тоғысқан токтардың алгебралық қосындысы нөлге тең.

Тізбектің (3-ші сурет) а түйінде

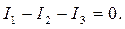
Мұнда түйнге бағытталған ток І₁ плюс таңбасымен, ал түйіннен шығып жатқан токтар І₂ және І₃ минус таңбасымен алынған.

Элементтермен ток жүрген кезде олардың бастапқы және соңғы нүктелерінің потенциалдарының айырымы, яғни кернеуі, элементтердің параметрінің қосындысы, яғни бастапқы және соңғы нүктелерінің патенциалдар айырымы, ЭҚК-ке тең болады.

Мысалы, сыртқы өңбой cE₁abR₄c үшін

(2)

мұндағы φ_е, φ_а, φ_b, φ_c, - нүктелердің потенциалдары.

Міне осы факт Кирхгофтың екінші заңы болып есептеледі. Оны былай жазуға болады:

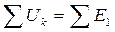не (3)

яғни тұйықталған өнбойда (контурда) ЭҚК-тердің алгебралық қосындысы кернеулердің түсіунің алгебралық қосындысына тең.

Тізбектерді Кирхгоф заңдарын пайдаланып есептеу тәртібі төмендегідей:

1. Схемада токтардың бағыты еркінше тандап алынады. Әдетте ЭҚК-тің бағытымен сәйкес алынады.

2. Өнбойды жүріп өту бағыты қалауынша алынады.

3. Кирхгофтың бірінші заңы бойынша бір түйіннен басқа түйіндердің барлығы үшін теңдеулер жазылады. Егер барлық түйіндер үшін де теңдеулер жазса, онда олардың біреуі басқалармен үйлесімді болады.

4. Жетіспеген теңдеулер (теңдеулер саны белгісіз шамалардың санына тең болуы керек) Кирхгофтың екінші заңы бойынша өзара тәуелсіз өнбойлар үшін жазылады.

5. Осы құрылған теңдеулер жүйесін шешіп, белгісіз токтарды анықтайды.

6. Токтың нақты бағыты анықталады, өйткені есепті шешу кезінде кейбір ток теріс мән алуы мүмкін. Минус таңбасы токтың еркінше таңдап алынған бағытының қателегін, яғни, оның бағытының керісінше екендігін көрсетеді. Егер ЭҚК көзінде ЭҚК-тің бағыты мен токтың бағыты сәйкес келмесе, онда бұл ЭҚК энергия көзі емес, керісінше электр қабылдағыш ретінде жұмыс істеп, электр энергиясын тұтынып тұр деп есептелінеді.

Белгісіз токтарды табу үшін Кирхгофтың бірінші заңы бойынша жазылған теңдеулер жүйесі:

а түйінде (4)

b түйінде 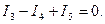(5)

Тізбекте бес ток бар. Бұл токтарды табу үшін тәуелсіз бес теңдеу құру керек. Ендеше қалған үш теңдеу Кирхгофтың екінші заңы бойынша тәуелсіз контур үшін жазылады (контурларды жүріп өту бағыты сағат тілімен бағыттас алынған):

І контурда (6)

ІI контурда (7)

IIІ контурда 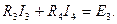(8)

Құрылған теңдеулер жүйесі (4) ...(8) Крамер өрнектері бойынша, Жордан-Гаусс немесе матрица әдістері қолданылып шешіледі. Көп белгісізді теңдеулер жүйесін электронды есептеу машинасының көмегімен шығару үшін матрицалық әдіс қолайлырақ.

Иллюстрация ретінде бірнеше мысалдар есептерін қарастырылған.