Момент силы. Условие равновесия тела, имеющего ось вращения

Моментом силы называют величину, способную вызывать и изменять вращение тела. При этом выделяют момент силы относительно точки (центра) и относительно оси.

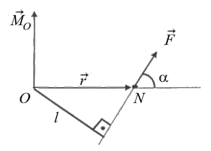
Рис. 4.2

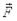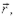Момент силы относительно неподвижной точки О представляет собой вектор определяемый векторным произведением радиуса-вектора проведенного из точки О в точку N приложения силы, на силу 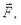рис. 4.2:

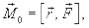(4.5)

где модуль момента силы М =Frsina=F×l(l¾плечо силы, то есть, кратчайшее расстояние между линией действия силы и точкой О). Направлен вектор 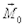перпендикулярно плоскости, проходящей через центр О и силу 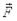в сторону, откуда поворот, вызываемый силой, виден против хода часовой стрелки.

Пример. Пусть точечный груз массой m подвешенный на нерастяжимой и невесомой нити длиной R к гвоздю, вбитому в потолок, совершает колебания около положения равновесия, рис. 4.3.

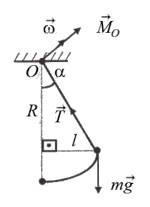
Рис. 4.3

Для рассматриваемого момента времени, когда груз возвращается в положение равновесия, вектор момента силы 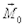совпадает по направлению с вектором угловой скорости 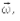его модуль равен M₀=mgl=mgRsina; момент силы натяжения нити Т всегда равен нулю, так как плечо этой силы равно нулю.

Момент силы относительно неподвижной оси zявляется алгебраической величиной, равной проекции на эту ось вектора 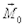момента силы, определенного относительно произвольной точки Она оси z, рис. 4.4.

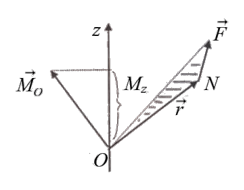
Рис. 4.4

Для решения обычных школьных задач достаточно рассмотрения момента силы относительно оси z, перпендикулярной плоскости, в которой лежат векторы 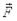и 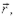рис. 4.5.

Направление оси при этом выбирают таким образом, чтобы момент был положительным, если он вызывает вращение по часовой стрелке.

Рис. 4.5

На любое тело могут действовать моменты различных сил, однако, для его равновесия, при наличии неподвижной оси вращения z, необходимо, чтобы алгебраическая сумма моментов всех сил, действующих на тело, относительно этой оси была равна нулю

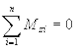(4.6)

или, формулируя более простым языком, моменты всех сил M_z, вращающих тело по часовой стрелке, должны быть равны моментам всех сил, вращающих его против часовой стрелки. При этом тело будет либо покоиться, либо равномерно вращаться вокруг оси.

Если у тела отсутствует закрепленная ось вращения, для его равновесия необходимо и достаточно выполнение условий (4.1) и (4.6) относительно любой возможной оси.

Условия равновесия часто используются для измерения неизвестных сил путем их сравнения с известными силами. Например, величину различных сил (гравитационных, электростатических, магнитных) измеряют, сравнивая их с силой упругости. В частности силу тяжести, действующую на тело, можно определить по показаниям пружинного динамометра.

Важной задачей статики является определение центра тяжести тела или системы тел.Центром тяжести является точка приложения равнодействующей всех сил тяжести, действующих на тело при любом его положении в пространстве (обычно находится путем пересечения линий подвеса тела). Сумма моментов всех элементарных сил тяжести относительно любой оси, которая проходит через центр тяжести, равна нулю.

У однородного тела центр тяжести находится на оси симметрии и пересечении осей симметрии, при этом он может оказаться вне самого тела (например, у кольца).

Пример. Два человека, массой m₁ = 60 кг и m₂ = 100 кг находятся в равновесии на разных концах горизонтально расположенной однородной прямоугольной доски, длиной l = 3 м и массой m₃ = 30 кг, имеющей одинаковую толщину и расположенной на поваленномдереве, рис. 4.6. На каком расстоянии х от правого края доски находится центр тяжести системы, состоящей из доски и двух человек или, иными словами, точка касания доски с деревом?

Рис. 4.6

Решение.Согласно условию (4.2) равнодействующая сил тяжести 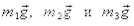по модулю равна модулю вектора 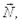т. е.m₁g+m₂g+m₃g=N. Данное выражение полезно для общих рассуждений и правильного построения рисунка, но для решения задачи вполне достаточно воспользоваться условием (4.6):

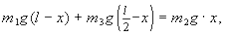(4.7)

откуда

Пример.Человек удерживает за один конец лестницу массой mтак, что она образует с горизонтом уголa,рис. 4.7. С какой силой 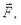направленнойперпендикулярно лестнице, он действует на нее в этом положении? Центр тяжести лестницы делит ее высоту пополам.

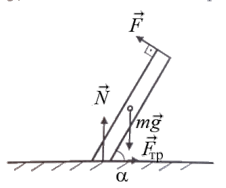
Рис. 4.7

Решение. Согласно условию (4.6)

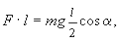(4.8)

где l ¾ длина лестницы. В результате имеем