Энергия. Закон сохранения механической энергии

Энергия ¾ это общая количественная мера движения и взаимодействия всех видов материи. Закон сохранения энергии гласит, что энергия не возникает из ничего и не исчезает бесследно, она может только переходить из одной формы в другую в эквивалентных количествах.

Различным формам движения материи соответствуют различные формы энергии: внутренняя, механическая, электромагнитная и т. д. Однако, это деление условно. Так, например, внутренняя энергия газа по сути представляет собой механическую и электромагнитную энергию отдельных молекул.

Рис. 3.5

Рассмотрим механическую систему. Пусть 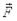¾единственная сила, действующая на движущуюся материальную точку (рис. 3.5). В любой точке траектории ее можно представить в виде касательной и нормальной к траектории составляющих

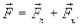(3.13)

Элементарная работа, совершенная силой 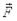на каждом перемещении

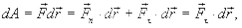(3.14)

тaк кaк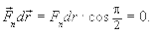

Сила 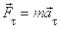имеет такое же направление, как и касательное ускорение 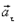и изменяет лишь абсолютную величину скорости dv=а_tdt,тогда

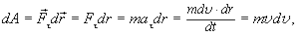(3.15)

или иначе

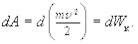(3.16)

Таким образом, работа, совершаемая силой 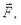изменяет характеристику движения частицы, равную

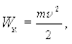(3.17)

которую называют кинетической энергией. Кинетическая энергия ¾ это энергия, обусловленная движением тела.

Очевидно, работа, совершаемая на участке траектории L_1-2 равна

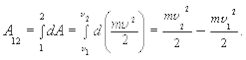(3.18)

Таким образом, при движении материальной точки в поле сил по траектории L₁₂ совершается работа. Можно показать, что для многих распространенных в природе сил величина этой работы зависит только от начального и конечного положения траектории и не зависит от ее вида. Такие силы называются консервативными или потенциальными. Поля таких сил также называют потенциальными или консервативными. Дляконсервативных сил справедливо следующее утверждение: работа консервативных сил по замкнутому пути равна нулю.

В механике к числу консервативных сил относятся гравитационная сила, а также сила упругости.

Для потенциальных полей можно ввести понятиепотенциальной энергии. Потенциальная энергия ¾ это такая функция координат поля консервативных сил, разность значений которой в любых точках поля равна работе сил поля при перемещении тела между этими точками. Для элементарных перемещений имеем

dA = -dW_п. (3.19)

Знак «минус» показывает, что работа потенциальной силы приводит к уменьшению потенциальной энергии тела.

Сила и скорость изменения потенциальной энергии в заданном направлении связаны между собой, так что

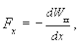(3.20)

то есть проекция консервативной силы на заданное направление равна скорости изменения потенциальной энергии, взятой с обратным знаком. Знак «минус» означает, что сила направлена в сторону убывания потенциальной энергии.

Можно показать, что численное значение потенциальной энергии тела в гравитационном поле земного тяготения, поднятого над поверхностью Земли на высоту h

W_п = mgh,

а потенциальная энергия упругих деформаций

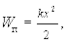
где k ¾ жесткость системы.

В целомпотенциальная энергия ¾ механическая энергия системы тел, определяемая их взаимным расположением и видом сил взаимодействия между ними.

При движении материальной точки в поле консервативных сил совершается работа, равная убыли потенциальной энергии

dA = -dW_п.

Одновременно работа сил поля приводит к изменению кинетической энергии частицы

dA = dW_к.

Тогда

dW_к = - dW_п, или

d(W_к + W_п) = 0

Введем полную механическую энергию частицы, равную сумме ее кинетической и потенциальной энергий

W = W_к + W_п (3.21)

В этом случае dW = 0 или

W = const (3.22)

Полученное соотношение представляет собойзакон сохранения механической энергии, который в общем виде формулируется следующим образом: полная механическая энергия замкнутой системы тел, взаимодействующих посредством консервативных сил, сохраняется неизменной.

Если в системе существуют неконсервативные силы, то часть механической энергии может перейти в другие виды энергии. Энергия в системе единиц СИ измеряется в джоулях.

Пример № 1. Тело массой m свободно падает без начальной скорости с высоты h на Землю. Считая поверхность Земли за нулевой уровень отсчета потенциальной энергии закон сохранения энергии запишется в следующем виде (тело упало на Землю):

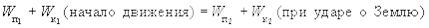
(3.23)

где по

Пример № 2. В примере № 1 тело толкнули вниз вдоль вертикали к поверхности Земли со скоростью v₀. В момент падения тела на Землю имеем

(3.24)

Пример № 3. Пусть в предыдущем примере в некоторый момент времени тело оказалось в результате падения на высоте h₁. Тогда закон сохранения энергии для этого случая будет иметь другой вид:

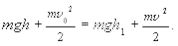(3.25)

Пример № 4. В примере № 3 учесть наличие силы сопротивления воздуха. В этом варианте получим

(3.26)