Закон сохранения импульса. Рассмотримзамкнутую систему, состоящую из n материальных точек (в механике ¾ это система, на тела

Рассмотримзамкнутую систему, состоящую из n материальных точек (в механике ¾ это система, на тела, входящие в которую не действуют внешние силы от тел вне данной системы, или когда геометрическая сумма воздействующих на систему внешних сил равна нулю).

Опытным путем установлено, что в такой системе взаимодействие материальных точек осуществляется так, что

(3.1)

где 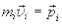¾импульс конкретной точки,

а 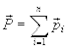¾полный импульс замкнутой системы материальных точек.

Таким образом, полный импульс замкнутой системы материальных точек не изменяется с течением времени. Это утверждение носит названиезакона сохранения импульса.

Конечно, под действием внутренних сил (сил внутри замкнутой системы), которые согласно III закону Ньютона попарно скомпенсированы, может меняться импульс отдельных частиц замкнутой системы, но для всей системы в целом полный импульс сохраняется.

Закон сохранения импульса является прямым следствием законов Ньютона. Это удобно показать на примере замкнутой системы, состоящей из двух тел.

Пример.Пусть замкнутая система состоит из двух взаимодействующих материальных точек, у которых по III закону Ньютона внутренние силы равны 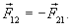Если время взаимодействия Dt,то 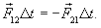Согласно II закону Ньютона импульс силы 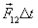равен приращению импульса второй точки 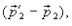а импульс силы 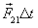¾первой 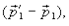откуда

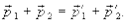(3.2)

Все тела, находящиеся на поверхности Земли всегда подвержены действию силы тяжести, но если ее воздействие скомпенсировано, то закон сохранения импульса выполняется. Он работает ивтом случае, когда изменение импульса за счет внешней силы значительно меньше, чем за счет импульсной (например, при столкновениях, взрывах и т. д.).

Для проекций импульсов на оси координат условие (3.1) записывается следующим образом:

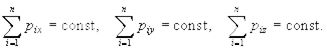(3.3)

Пример.Два хоккеиста, движущиеся навстречу друг другу по гладкой горизонтальной поверхности, сталкиваются и далее перемещаются вместе (рис. 3.1). Первый хоккеист, масса которого m₁ = 120 кг двигался со скоростью v₁ = 3 м/с, а скорость второго при массе m₂ = 80 кг была равна v₂ = 6 м/с. В каком направлении и с какой скоростью о они будут двигаться после столкновения?

Рис. 3.1

Решение. Применим закон сохранения импульса, предположив, что направление движения первого хоккеиста совпадает с направлением оси х,и что горизонтальные силы практически отсутствуют. В проекции на эту ось закон запишется в виде

m₁v₁ - m₂v₂ = (m₁ + m₂)v, (3.4)

откуда

Знак «минус» показывает, что после столкновения хоккеисты будут двигаться в направлении движения второго хоккеиста.

Пример. Призма, масса которой М, а угол уклона a, находится на гладкой горизонтальной поверхности льда. На призме стоит человек, масса которого m (рис. 3.2). С какой скоростью и будет двигаться призма, если человек пойдет вверх по поверхности призмы со скоростью и относительно нее? Трением между призмой и льдом пренебречь.

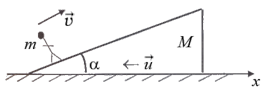
Рис. 3.2

Решение. Согласно закону сохранения импульса, записанному в проекции на горизонтально направленную ось координат х (рис. 3.2), имеем m(vcosa + и) + М × и = 0, (3.5)

откуда

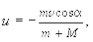
где и ¾ проекция скорости призмы на ось х,знак которой раскрывается в ответе, или, как второй возможный вариант, считая v и и ¾ модулями соответствующих векторов, с учетом направления движения тел системы, запишем

m(vcosa - и) - М × и = 0, (3.6)

откуда получим значение модуля вектора и

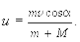
Закон сохранения импульса объясняет такие явления, как реактивное движение, отдача при выстреле, движение лодки с помощью весел и т. д.

Реактивное движение ¾ это движение тела (ракеты), которое возникает в результате выброса им вещества. Законы движения тел переменной массы (реактивное движение) были исследованы русскими учеными И.В. Мещерским (1859-1935 гг.) и К.Э. Циолковским (1857-1935 гг.).