Система отсчета. Язык кинематики
Раздел 1. Механика
Тема 1. Кинематика
Основные вопросы для повторения:
1. Что такое физика?
2. Дайте определение основных разделов классической механики.
3. Введите понятие системы отсчета.
4. Дайте определение основных кинематических параметров: путь, перемещение, скорость и ускорение.
5. Что такое траектория?
6. Рассмотрите на примерах касательное и нормальное ускорение тел.
7. Какие виды движения Вы знаете?
8. Запишите основные уравнения равномерного и равнопеременного движений, дайте их графическое представление.
9. Введите основные параметры вращательного движения.
Система отсчета. Язык кинематики
Классическая механика ¾ раздел физики, в котором изучаются закономерности механического движения тел и причины, влияющие на это движение. При этом под механическим движением обычно понимается изменение взаимного расположения тел или их частей относительно друг друга с течением времени.
Физика, как и любая другая наука, использует при рассмотрении конкретных ситуаций довольно много весьма полезных приближений ¾ абстракций. Например, при решении целого ряда задач, связанных с движением тела пренебрегают его деформацией, вводя понятие абсолютно твердого тела, у которого взаимное расположение его частиц не меняется при движении, или используют понятие материальная точка, под которой имеют ввиду тело, размерами которого в данной задаче можно пренебречь, а внутреннюю структуру не учитывать.
Механика обычно делится на три больших раздела: кинематику, динамику и статику.
Кинематика изучает движение тела без учета причин, вызывающих и изменяющих движение. Динамика эти причины исследует, формируя законы движения. Статика рассматривает условия равновесия тел и, по сути, законы статики являются частным случаем законов динамики.
Наша первая лекция посвящена кинематике. Остановимся на основных понятиях этого раздела.
Механическое движение относительно. Говоря о движении какого-либо тела, необходимо указать относительно каких других тел перемещается рассматриваемый объект. Тело (или совокупность тел), которое условно считается неподвижным и по отношению к которому рассматривается движение других тел называется телом отсчета. Движение тел рассматривают в системе отсчета, представляющей собой тело отсчета, жестко связанную с ним систему координат и выбранный способ измерения времени.
Пример. Пусть материальная точка переместилась за время Dt из позиции N в позицию M, которые мы фиксируем в прямоугольной (декартовой) системе координат, рис. 1.1.
В заданный момент времени положение точки по отношению к этой системе характеризуется тремя координатами х, у, zили радиусом-вектором 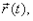 проведенным из начала координат в данную точку.
проведенным из начала координат в данную точку.

Рис. 1.1
Движение материальной точки определяется скалярными уравнениями
x = x(t); y = y(t); z = z(t), (1.1)
которым соответствует векторное уравнение
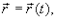 (1.2)
(1.2)
где 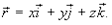 В данном обозначении
В данном обозначении 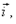
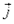 и
и 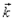 являются единичными векторами (ортами) координатных осей х, у и z.
являются единичными векторами (ортами) координатных осей х, у и z.
Совокупность последовательных положений, которые занимает материальная точка при своем движении, называетсятраекторией (годограф вектора 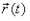 ).
).
Путь ¾ это неотрицательная скалярная величина, равная расстоянию, пройденному материальной точкой вдоль ее траектории (s или в обозначении на рис. 1.1 ¾ Ds).
Вектор 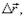 проведенный из начального положения движущейся точки (в момент времени t, см. рис. 1.1) в положение, занимаемое ей в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени Dt), называетсяперемещением (при этом
проведенный из начального положения движущейся точки (в момент времени t, см. рис. 1.1) в положение, занимаемое ей в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени Dt), называетсяперемещением (при этом 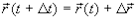 ).
).
При прямолинейном движении модуль перемещения 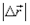 равен пройденному телом пути Ds, если движение происходило в неизменном направлении.
равен пройденному телом пути Ds, если движение происходило в неизменном направлении.
Векторную величину, характеризующую направление и быстроту перемещения материальной точки относительно тела отсчета, называютскоростью. В нашем случае
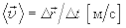 (1.3)
(1.3)
является вектором средней скорости, его направление совпадает с направлением 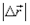 и зависит от Dt. При неограниченном уменьшении Dtсредняя скорость
и зависит от Dt. При неограниченном уменьшении Dtсредняя скорость 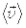 стремится к предельному значению, которое получило названиемгновенной скорости (начало дифференциального исчисления в математике):
стремится к предельному значению, которое получило названиемгновенной скорости (начало дифференциального исчисления в математике):
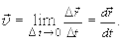 (1.4)
(1.4)
Таким образом,мгновенная скорость 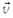 есть векторная величина, равная первой производной радиуса-вектора движущейся материальной точки по времени. В пределе (см. рис. 1.1) вектор
есть векторная величина, равная первой производной радиуса-вектора движущейся материальной точки по времени. В пределе (см. рис. 1.1) вектор 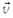 будет совпадать с касательной к траектории в направлении движения, путьDsбудет практически неотличим от
будет совпадать с касательной к траектории в направлении движения, путьDsбудет практически неотличим от 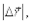 т. к.
т. к. 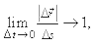 поэтому модуль мгновенной скорости можно представить в виде:
поэтому модуль мгновенной скорости можно представить в виде:
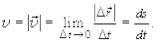 (1.5)
(1.5)
Часто приходится рассчитыватьсреднюю путевую скорость(скалярная величина)
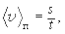 (1.6)
(1.6)
которую на транспорте называют маршрутной скоростью (маршрутная скорость московского метро составляет около 40 км/ч).
Пример. Катер двигался по течению реки из пункта А в пункт Б со скоростью v1,а обратно со скоростью v2. Найти маршрутную скорость катера при движении.
Решение: 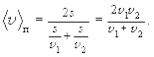
Скорость тел при движении может изменяться. Физическую величину, характеризующую быстроту изменения скорости по модулю и направлению, назвалиускорением.
Средним ускорением является отношение
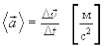 (1.7)
(1.7)
мгновенным ¾ первая производная скорости по времени
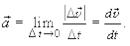 (1.8)
(1.8)
В декартовой системе координат модуль мгновенного ускорения определяется как
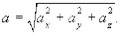 (1.9)
(1.9)
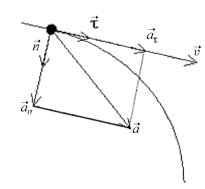
Рис. 1.2
Как показывает эксперимент, вектор ускорения при криволинейном движении направлен под произвольным углом к направлению вектора скорости (рис. 1.2, подробнее в динамике). Его можно разложить на две составляющих: 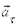 ¾касательное или тангенциальное ускорение и
¾касательное или тангенциальное ускорение и 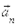 ¾нормальное или центростремительное ускорение, то есть
¾нормальное или центростремительное ускорение, то есть
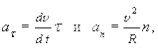 (1.10)
(1.10)
при этом 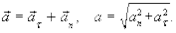
В данном случае 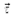 и
и 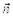 ¾единичные векторы в направлении соответственно вдоль и перпендикулярно вектору скорости, R¾радиус кривизны траектории. Дело в том, что любой небольшой участок произвольно искривленной линии можно приближенно рассматривать как дугу окружности, которая будет сливаться с линией на бесконечно малом ее участке. Радиус этой окружности и получил название радиуса кривизны траектории.
¾единичные векторы в направлении соответственно вдоль и перпендикулярно вектору скорости, R¾радиус кривизны траектории. Дело в том, что любой небольшой участок произвольно искривленной линии можно приближенно рассматривать как дугу окружности, которая будет сливаться с линией на бесконечно малом ее участке. Радиус этой окружности и получил название радиуса кривизны траектории.
Нормальное ускорение аn характеризует быстроту изменения скорости по направлению,касательное аt¾ по модулю.
Пример. Баллистическое движение, рис. 1.3.
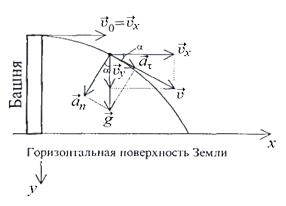
Рис. 1.3
Примечание:для случая свободного падения (в вакууме) Галилей постулировал, что все тела будут падать с одинаковым постоянным ускорением 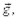 его значение равно g»9 8 м/с2.
его значение равно g»9 8 м/с2.
Пример.Равномерное  движение точки по окружности, рис. 1.4.
движение точки по окружности, рис. 1.4.
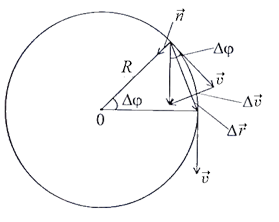
Рис. 1.4
Примечание: из подобия треугольников имеем
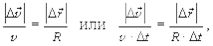
откуда 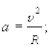 в пределе при Dt®0,
в пределе при Dt®0, 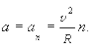
Дата добавления: 2015-10-19; просмотров: 923;
