Равнопеременное движение

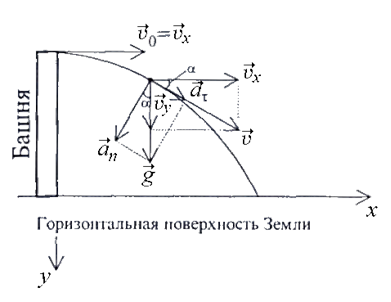
Равнопеременное движениеточки соответствует условию, когда касательное ускорение (в случае прямолинейного движения полное ускорение) постоянно. Важно понять, что движение с постоянным ускорением может и не быть прямолинейным, например, при невертикальном бросании тела с башни (см. рис.) полное ускорение 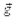всегда направлено к центру Земли, если, конечно, отсутствует боковое усилие в процессе его полета.

В качестве примера равнопеременного движения рассмотрим движение материальной точки в направлении оси х, рис. 1.6.

Рис. 1.6

Если при равнопеременном прямолинейном движении направление вектора ускорения 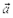совпадает с направлением вектора начальной скорости 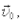то такое движение называется равномерно ускоренным (обычно называют просто ¾равноускоренным), если ¾противоположно, то равномерно замедленным(равнозамедленным).

Из определения ускорения имеем:

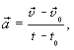(1.20)

если для удобства анализа возьмем t₀ = 0, то получим

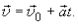(1.21)

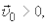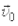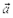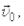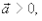В нашем примере (рис. 1.6) так как вектор направлен вдоль положительного направления оси х. Если ускорение совпадает с направлением вектора то если не совпадает, то 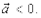Следует иметь в виду, что при 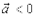величина вектора скорости может оказаться и отрицательной. Можно внести знак плюс или минус в саму формулу (1.21), тогда

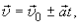(1.22)

в этом варианте v ¾ величина скорости материальной точки и а представляет собой модуль ее ускорения.

С учетом (1.22) координата х может фиксироваться с помощью уравнения

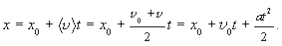(1.23)

Если направление вектора 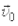по оси х имеет два варианта (вдоль и против положительного направления), то выражение (1.23) запишется как

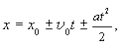(1.24)

где v₀ ¾ модуль вектора начальной скорости.

Если в системе уравнений (1.22), (1.23) исключить время, то получим весьма полезное при решении ряда задач уравнение (следует запомнить):

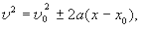(1.25)

которое при движении в одном направлении имеет вид¹

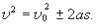(1.26)

Мы рассмотрели движение материальной точки вдоль одной из осей координат. Это удобно, так как при прямолинейном движении декартову систему координат можно развернуть таким образом, чтобы движение происходило в направлении выбранной оси.

В общем случае, если мы имеем в пространстве векторы, характеризующие движение:

равномерное прямолинейное

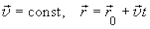(1.27)

равноускоренное движение 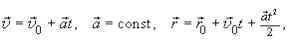(1.28)

то для построения графиков движения и проведения расчетов (векторную функцию нельзя изобразить в виде графика) осуществляют проекцию векторов на оси координат.