Равномерное движение. Если материальная точка за равные, сколь угодно малые промежутки времени, проходит одинаковые пути, то такое ее движение называетсяравномерным

Если материальная точка за равные, сколь угодно малые промежутки времени, проходит одинаковые пути, то такое ее движение называетсяравномерным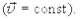

В случае равномерного прямолинейного движения сохраняется и направление вектора скорости, то есть

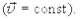(1.11)

Согласно (1.5) модуль вектора скорости можно представить как первую производную от пути по времени, откуда

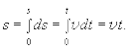(1.12)

Пример. Материальная точка равномерно движется вдоль прямой.

Если ось координат х взять вдоль направления движения, то проекция скорости точки v_х, будет равна величине вектора скорости v_х = v, поэтому, опуская индекс х, запишем

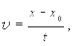(1.13)

где х₀ ¾ координата материальной точки в момент времени t = 0.

В результате имеем

x = x₀ + vt. (1.14)

Если скорость направлена в направлении противоположном оси х, то часто записывают

x = x₀ - vt, (1.15)

где под v уже однозначно понимают модуль вектора скорости, или же в выражении (1.15) сохраняют знак плюс, в таком случае считая v величиной вектора скорости.

Рассмотрим равномерное движение при вращении какого-либо тела, выделяя в нем конкретную точку, поворачивающуюся относительно, например, оси у на угол Djили взяв в качестве примера обращение материальной точки относительно этой же оси, рис. 1.5 (точка O¾начало координат, точка O'¾центр окружности, ось у ¾ось вращения). При вращательном движении вводят понятие ¾вектор угла поворота 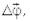который направлен вдоль оси вращения. Ориентация этого вектора определяется правилом буравчика (рукоятка буравчика вращается вслед за рассматриваемой точкой ¾рис. 1.5, а направление его поступательного движения задает направление вектора 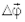).При векторной форме задания угла поворота, его величина считается небольшой.

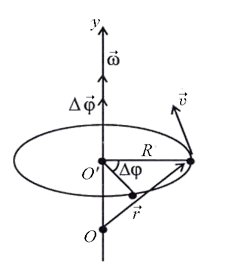
Рис. 1.5

Векторная величина w (омега), характеризующая быстроту поворота точки, называется ееугловой скоростью:

Векторная величина w (омега), характеризующая быстроту поворота точки, называется ееугловой скоростью:

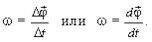(1.16)

При равномерном вращении угловая скорость постоянна:

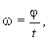(1.17)

где j ¾ угол поворота за время t. Угол поворота измеряется в радианах (рад), угловая скорость (рад/с).

При равномерном вращении постоянен и модуль линейной скорости |v| (упрощенно просто v). Исходя из того, что радиан соответствует расстоянию по окружности, равному ее радиусу имеем:

v = w × R (1.18)

В более общем плане v = [w, r].

Равномерное вращение характеризуется периодом вращения Т, под которым понимают промежуток времени за который рассматриваемая точка поворачивается на угол j = 2p. В результате можем записать

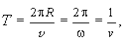(1.19)

где v ¾ частота вращения, равная числу оборотов в единицу времени. Модуль угловой скорости w часто называют круговой частотой.