Законы Ньютона. В основе динамики лежат три закона Ньютона, сформулированные в 1687 г

В основе динамики лежат три закона Ньютона, сформулированные в 1687 г. в его знаменитой работе «Математические начала натуральной философии». Рассмотрим последовательно эти законы.

Системы координат можно связывать с различными телами. Особо важный класс тел представляют невзаимодействующие или свободные тела. Свободным называют тело, настолько удаленное от всех остальных, что их воздействие на движение данного тела пренебрежимо мало. Размерами свободных тел часто можно пренебречь, считая их материальными точками. Свяжем с группой одинаково движущихся свободных тел систему координат. В такой системе отсчета, как показывает опыт, все другие свободные тела движутся равномерно и прямолинейно. Таким образом, для свободных тел справедливо утверждение: существуют системы отсчета, в каждой из которых невзаимодействующие тела могут двигаться равномерно и прямолинейно (или, как частный случай такого движения, находиться в состоянии покоя). Это утверждение носит названиеI закона Ньютона или закона инерции (основные выводы получены еще Г. Галилеем). Системы отсчета, связанные со свободно движущимися телами называютинерциальными системами отсчета. При условии введения меры механического воздействия ¾ силы, этот закон можно сформулировать следующим образом:материальная точка сохраняет состояние покоя или равномерного прямолинейного движения, если на нее не действуют никакие силы или действие сил взаимно скомпенсировано, то есть

если 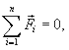то v=0 или v=const, (2.1)

где 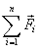¾равнодействующая всех сил, приложенных к данной точке. Таким образом, сила не накапливается, а ее компенсация приводит к равномерному прямолинейному движению.

Взаимодействие тел, как показывает опыт, вызывает изменение их скоростей

v_i = v_i(t). (2.2)

и, как следствие, их импульсов. Импульсом тела называют динамическую характеристику его движения, равную

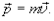(2.3)

Это векторная величина, которая в каждый момент времени совпадает по направлению с вектором мгновенной скорости. Коэффициент пропорциональности в (2.3) характеризует объект движения и его называют массой тела (измеряется в системе единиц СИ в килограммах ¾ кг).

Таким образом, в процессе воздействия на данную материальную точку других тел ее импульс изменяется. В этом плане в качестве меры взаимодействия тел выбирается физическая величина, которая выражается через скорость изменения импульса и которую в динамическом понимании назвали силой:

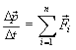или точнее 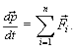(2.4)

Представленное равенство (2.4) носит названиеII закона Ньютона. Это фундаментальный закон классической физики:скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил. Его можно записать и в другой форме

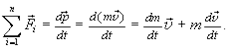(2.5)

Если m = const, то

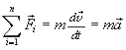(2.6)

или

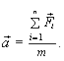(2.7)

Ускорение материальной точки пропорционально равнодействующей всех приложенных к ней сил, обратно пропорционально ее массе и сонаправлено с равнодействующей сил (II закон Ньютона). Согласно (2.7) сила измеряется в кг × м/с, эта единица измерения получила название ньютон (Н).

Выражение (2.7) позволяет конкретизировать понятие массы. Из этого уравнения видно, что при одинаковой величине силы, воздействующей на тело, ускорение материальной точки тем меньше, чем больше ее масса. Свойство тел сохранять состояние покоя или равномерного прямолинейного движения называется инертностью (инерцией). Таким образом, материальная точка, получившая меньшее ускорение, будет более инертной, т. е. масса, входящая в формулу II закона Ньютона, характеризует инерцию тела и ее называют инертной массой. Опыт показывает, что с массой также связана способность тел притягиваться друг к другу (гравитационная масса).