Тема 4. Дисконтирование денежных потоков
Временная ценность денежных вложений относится к одной из основных концепций, используемых в инвестиционном анализе. Необходимость учета временного фактора заставляет особое внимание уделять оценке базовых финансовых показателей. Разность в оценке текущих денежных средств и той же их суммы в будущем может быть вызвана:
- негативным воздействием инфляции, в связи с чем происходит уменьшение покупательной способности денег;
- возможностью альтернативного вложения денежных средств и их реинвестирования в будущем (фактор упущенной выгоды);
- ростом риска, связанного с вероятностью невозврата инвестированных средств (чем длительнее срок вложения капитала, тем выше степень риска);
- потребительскими предпочтениями (лучше получить меньше доход в ближайшем периоде, чем ожидать большее, но в отдаленной перспективе).
В планируемом периоде анализ предстоящей реализации различного вида инвестиционных проектов может осуществляться по двум противоположным направлениям. С одной стороны, определяется будущая стоимостная оценка первоначальной величины инвестиций и доходов (дивидендов, процентов, прибыли, денежных потоков и пр.), полученных в результате осуществления этих капиталовложений. С другой стороны, приращенные в ходе инвестирования денежные средства оцениваются с позиции их текущей (настоящей) стоимости. В соответствии с этим в финансово-инвестиционном анализе используются операции дисконтирования и наращения капитала. Принципиальная схема инвестиционного анализа, осуществляемого с учетом временной ценности денежных вложений, представлена на рис. 1.
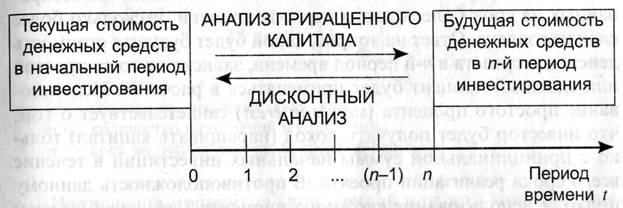
Рис. 1. Схема проведения инвестиционного анализа с использованием операций наращений и дисконтирования капитала
При разработке оптимальных финансовых решений в определенных ситуациях требуется проведение оценки будущей стоимости инвестированных денежных средств. Нахождение будущей стоимости денежных средств по истечении одного периода времени и при известном значении темпа их прироста осуществляется по следующей формуле:
FV1 = PV + PV*r = PV(1+r),
где FV1 — будущая стоимость денежных средств в конце первого периода инвестирования (t + 1), тыс. руб.;
PV— первоначальная (принципиальная) сумма денежных средств, инвестированных в начальный период времени (t = 0), тыс. руб.;
r — темп прироста денежных средств, коэф.
Процесс, в котором при заданных значениях PV и r необходимо найти величину будущей стоимости инвестированных средств к концу определенного периода времени (FV), называется операцией наращения. В практике инвестиционного анализа «темп прироста» денежных средств принято называть «процентом», «ставкой процента» или «нормой рентабельности», а первоначальную сумму денежных средств — «текущей стоимостью» (PV).
Из предыдущей зависимости FV1 от PV темп прироста денежных средств исчисляется по формуле
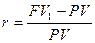
Оценка будущей стоимости денежных вложений, инвестированных на срок более одного периода времени, несколько более сложная задача. Ответ на вопрос, какой будет будущая стоимость денежных средств в n-й период времени, зависит от того, простой или сложный процент будет применяться в расчетах. Использование простого процента (simple interest) свидетельствует о том, что инвестор будет получать доход (наращивать капитал) только с принципиальной суммы начальных инвестиций в течение всего срока реализации проекта. В противоположность данному подходу использование сложного процента (compound interest) свидетельствует о том, что полученный доход (проценты, дивиденды или пр.) периодически добавляется к сумме начальной инвестиции, в результате помимо первоначальной суммы денежных средств процент берется также из накопленной в предыдущих периодах суммы процентных платежей или любого другого вида доходов. В математическом исчислении операция наращения с использованием сложных процентов к концу второго периода реализации проекта определяется по формуле
FV2 = PV(1 +r)(l + r) = PV(1 + r)2.
В конце n-го периода времени будущая стоимость денежных средств (FVn) исчисляется по следующей формуле:
FVn = PV (1 + r)n.
Данная формула расчета FVn является базовой в инвестиционном анализе. Для облегчения процедуры нахождения показателя FVn предварительно рассчитывается величина множителя (1 + r)n при различных значениях r и п. В этом случае FVn определяется по формуле
FVn = PV*FVIFr, n,
где FVIF r, n — фактор (множитель) будущей стоимости денежных вложений, коэф.
В инвестиционном анализе под стандартным временным интервалом принято рассматривать один год. В случае когда дополнительно оговаривается частота выплаты процентов по вложенным средствам в течение года, формула расчета будущей стоимости инвестированного капитала может быть представлена в следующем виде:
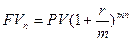
где r — годовая процентная ставка, коэф.; т — количество начислений в году, един.; п — срок вложения денежных средств, год.
Начисление процентов (дивидендов или др.) может осуществляться ежедневно, ежемесячно, поквартально, раз в полугодие и раз в год. Характерно, что чем больше количество раз в течение года будут начисляться проценты, тем больше будет FV в конце n-го периода времени. Для целей анализа отношение r/m принято рассматривать в качестве процентной ставки, а произведение п*т — в качестве срока инвестирования. Этот случай соответствует следующей экономической ситуации.
Коммерческая организация приняла решение инвестировать на пятилетний срок свободные денежные средства в размере 30 тыс. руб. Имеются три альтернативных варианта вложений. По первому варианту средства вносятся на депозитный счет банка с ежегодным начислением сложных процентов по ставке 20% годовых. По второму варианту средства передаются сторонней организации в качестве займа, при этом на переданную в долг сумму ежегодно начисляется 25%. По третьему варианту средства помещаются на депозитный счет коммерческого банка с начислением сложных процентов по ставке 16% годовых ежеквартально. Если не учитывать уровень риска, наилучший вариант вложения денежных средств может быть определен при помощи показателя FVn. По варианту I: FVn = 30 тыс. руб. * (1 + 0,2)5 = 74,7 тыс. руб. По варианту II: FVn = 30 тыс. руб. + 5*(30 тыс. руб.*0,25) = = 67,5 тыс. руб. По варианту III: FVn = 30 тыс. руб. * (1 + 0,16/4)5*4 = = 65,7 тыс. руб. В данных условиях первый вариант более предпочтителен для предприятия.
Наращение денежных средств имеет свое максимальное (предельное) значение, когда интервал наращения становится бесконечно малым (количество начислений в году стремится к бесконечности). В этом случае показатель FVn определяется по формуле
FVn = PV*еr*n,
где е — трансцендентное число е, равное 2,718281... (постоянная величина).
В ходе анализа эффективности двух или более инвестиций с различными интервалами наращения капитала необходимо использовать обобщающий финансовый показатель, позволяющий проводить их объективную сравнительную оценку. Таким показателем является эффективная годовая процентная ставка (EAR), рассчитываемая по формуле

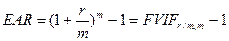
В финансовых расчетах часто возникает потребность в оценке текущей стоимости будущих денежных потоков (PV). Данного рода процедуры осуществляются с целью определения ценности будущих поступлений от реализации того или иного проекта с позиции текущего момента времени. Процесс конвертирования планируемых к получению в предстоящих периодах времени денежных потоков в их текущую стоимость называется операцией дисконтирования. Процентная ставка, используемая в подсчете PV, называется дисконтной ставкой. Показатель текущей стоимости рассчитывается по формуле
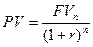
Отношение 1/(1 + r)n известно как фактор (множитель) текущей стоимости (PVIFr,n). Формула расчета PV уравнивает, с точки зрения инвестора, ценность денежных средств сегодня и ожидаемого к получению денежного потока в будущем.
Как и в случае с наращением капитала, для оптимального принятия финансовых решений чрезвычайно важно знать и учитывать в анализе временной интервал дисконтирования. Если начисление процентов планируется (или произошло) более одного раза в год, формулу для нахождения PV необходимо представить в следующем виде:
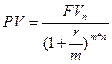
Возможности практического использования показателя PV раскрываются в различных экономических ситуациях, когда возникает необходимость обоснования финансово-инвестиционных решений с учетом временной ценности денежных вложений. Одна из типичных ситуаций в инвестиционной деятельности хозяйствующих субъектов представлена ниже.
Коммерческая организация планирует приобрести помещения под склад и офис. Эксперты оценивают будущую стоимость недвижимости в размере 10 млн. руб. По банковским депозитным счетам установлены ставки в размере 32% с ежегодным начислением сложных процентов и 28% с ежеквартальным начислением сложных процентов. При помощи показателя PV можно определить, какую сумму средств необходимо поместить на банковский депозитный счет, чтобы через два года получить достаточную сумму для покупки недвижимости. Расчет оптимального варианта инвестирования осуществляется следующим образом: в первом случае PV = 10 млн .руб. * (1/[1 + 0,32]2) = 5,739 млн. руб.; во втором случае PV = 10 млн руб. * (1/[1 + 0,28/4]2*4) = 5,82 млн. руб. Очевидно, что более выгодным для предприятия является вложение меньшей суммы средств, т.е. первый вариант.
При заданной величине дисконтной ставки текущая стоимость денежных потоков будет достигать своего минимально возможного значения при непрерывном дисконтировании. В этом случае (когда 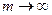 ) текущая стоимость исчисляется по формуле
) текущая стоимость исчисляется по формуле
FVn = PV*е-r*n
На практике встречается ситуация, когда необходимо оценить денежные потоки, произведенные инвестицией в различные периоды времени. В этой связи одной из важных задач, встречающихся перед специалистами в области инвестиционного анализа, является оценка аннуитета.
Аннуитет представляет собой равные по величине денежные потоки, возникающие в каждом периоде определенного временного интервала. Примером аннуитета могут служить периодическая выплата процентов по заемным средствам финансирования, купонного дохода по облигациям, перечисление арендной платы и пр. Поступления и выбытия средств могут происходить как в начале (обязательный аннуитет), так и в конце каждого конкретного периода (обыкновенный или отложенный аннуитет). В практике финансовых расчетов наиболее часто используется обыкновенный аннуитет. Будущая стоимость обыкновенного аннуитета (FVAn) продолжающегося в течение п периодов определяется по следующей формуле:
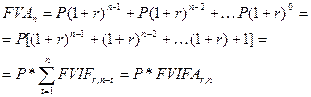
где Р — периодические поступления или выбытия равных по величине денежных средств, тыс. руб.;
FVIFAr,n — фактор (множитель) будущей стоимости обыкновенного аннуитета, коэф.
Множитель FVIFArn может быть рассчитан по следующей формуле:
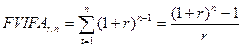
Данный показатель отражает будущую стоимость одной денежной единицы в конце срока реализации инвестиционного проекта.
Порядок исчисления FVA,, рассмотрен на рис. 2.
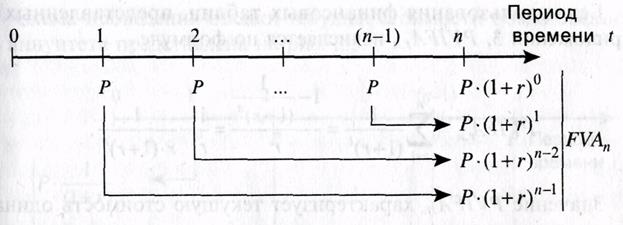
Рис. 2. Схема подсчета будущей стоимости обыкновенного аннуитета
Компания ABC планирует через 5 лет осуществить замену ведущего оборудования. Предполагается, что инвестиционные затраты составят 2110 тыс. руб. Чтобы накопить необходимую сумму средств, предприятие из прибыли, остающейся в его распоряжении, ежегодно перечисляет средства на депозитный счет банка. Ставки по депозитным счетам в различных банках составляют 24 и 32% (с начислением процентов раз в год). Чтобы определить величину ежегодных отчислений, необходимо использовать формулу будущей стоимости обыкновенного аннуитета. По первому варианту (при r - 24%) Р = 2110 тыс. руб. / FVIFA24,5 = 262,2 тыс. руб. По второму варианту (при r – 32%) Р = 2110 тыс. руб. / FVIFA32,5 = 224,5 тыс. руб.
Текущая стоимость аннуитета (PVAn) равна сумме денежных средств, дисконтированных индивидуально по каждому периоду времени. Для оценки PVAn используется следующая формула:
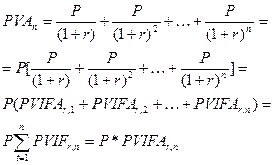
где PVIFArn — фактор (множитель) текущей стоимости обыкновенного аннуитета, коэф.
PVIFAr,n исчисляется по формуле
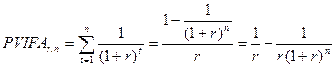
Значение PVIFAr,n характеризует текущую стоимость одинакового по величине денежного потока (в размере одной денежной единицы), регулярно возникающего на протяжении установленного срока (n) с определенной нормой доходности (r) на вложенные средства.
Применение формулы текущей стоимости аннуитета в инвестиционном анализе можно проиллюстрировать следующим примером.
Фирма «Апекс» приобретает новое компьютерное оборудование за 25,3 тыс. руб., при этом планируется в течение ближайших 5 лет ежегодно получать экономию затрат по ведению бухгалтерского учета в размере 10 тыс. руб. Средние ставки по банковским депозитам составляют 35% годовых. Чтобы оценить целесообразность данной инвестиции, необходимо рентабельность инвестиции сравнить с альтернативными возможностями вложения средств (в нашем случае речь идет о банковском депозите). Искомый показатель рентабельности можно найти при помощи фактора текущей стоимости аннуитета, а именно:
PVIFAr,5 = 25,3 тыс. руб. / 10 тыс. руб. = 2,53.
При стандартных значениях PVIFAr,n рентабельность инвестиции составит 28%. Отсюда следует, что экономически более целесообразным будет вложение этой же суммы средств на депозитный счет банка.
Необходимо помнить, что расчет показателей FVAn и PVAn, основанный на схеме начисления сложных процентов, не допускает изъятия полученных денежных средств до окончания срока действия аннуитета.
При известных значениях PVAn и PVIFAr,n величина Р определяется по формуле
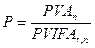
Схема проведения оценки текущей стоимости обыкновенного аннуитета представлена на рис. 3.
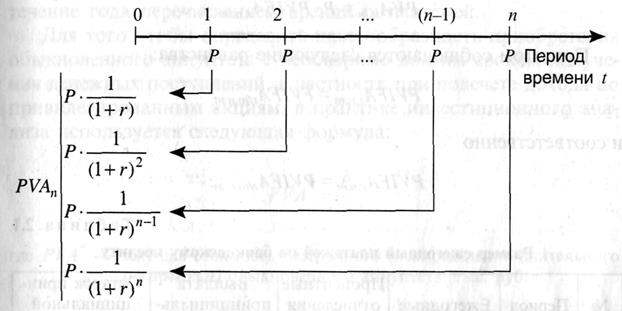
Рис. 3. Схема подсчета текущей стоимости обыкновенного аннуитета
Формула расчета PVAn может быть эффективно использована для выделения процентных платежей и суммы основного долга из общей величины средств, идущих на погашение долгосрочных или краткосрочных обязательств. Например, организация получает банковский кредит в размере 150 млн руб. на пятилетний срок с уплатой 10%, начисляемых ежегодно. При этом погашение кредита и процентных платежей осуществляется равными взносами в течение пяти лет, начиная с конца первого года. Расчет ежегодных платежей по банковскому кредиту (Р) осуществляется с использованием формулы текущей стоимости аннуитета: Р = 150 млн. руб. / PVIFAl0,5 = 150 млн руб. / 3,7908 = 39,6 млн руб. В дальнейшем выделение из общей суммы Р процентных и принципиальных платежей можно провести в аналитической табл. 1.
Таблица 1. Размер ежегодных платежей по банковскому кредиту
| № п/п | Период времени (t), год | Ежегодные начисления (Р), млн. руб. | Процентные отчисления (при r=10%), млн. руб. | Выплата принципиальной суммы кредита, млн. руб. | Остаток принципиальной суммы кредита, млн. руб. |
| А | |||||
| - | - | - | - | 150,0 | |
| 39,569 | 15,0 | 24,569 | 125,431 | ||
| 39,569 | 12,543 | 27,027 | 98,404 | ||
| 39,569 | 9,84 | 29,729 | 68,675 | ||
| 39,569 | 6,867 | 32,702 | 35,973 | ||
| 39,569 | 3,597 | 35,972 | 0,001 | ||
| Итого | 197,845 | 47,847 | 149,999 | - |
Если интервал дисконтирования или частота начисления процентов для аннуитета меньше одного года (в качестве примера можно привести выплату процентов по облигациям), формулы для нахождения FVAn и PVAn должны предстать в следующем виде:
FVAn,m = P*FVIFAr,n,m
и соответственно для текущей стоимости обыкновенного аннуитета:
PVAn,m = P*PVIFAr,n,m.
При этом соблюдаются следующие равенства:
FVIFAr,n,m = FVIFAr/m,n*m
и соответственно
PVIFAr,n,m = PVIFAr/m,n*m
В качестве практического примера использования формулы текущей стоимости аннуитета с многократным начислением процентов в течение года можно представить ситуацию с выбором наилучшего варианта выплаты арендных платежей. По варианту А фирма, заключающая двухлетний договор аренды, ежемесячно выплачивает 32 тыс. руб., по варианту В платежи производятся раз в год в размере 384 тыс. руб. В качестве релевантной процентной ставки используется годовая ставка инфляции, равная 12%. По варианту A: PVA2 = 32 тыс. руб. * PVIFA 12,2,12 = 32 тыс. руб. * PVIFA1,24 = 32 тыс. руб. * 21,2434 = 679,8 тыс. руб. По варианту В: PVA2 = 384 тыс. руб. * PVIFA12,2 = 384 тыс. руб. * 1,6901 = 649,0 тыс. руб. Для данного предприятия экономически более выгодны условия с однократным в течение года перечислением арендных платежей.
Для того чтобы определить целесообразность приобретения обыкновенного аннуитета с необозримо долгим сроком получения денежных поступлений, в частности при подсчете дохода по привилегированным акциям, в практике инвестиционного анализа используется следующая формула:
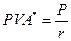
где PVA* — текущая стоимость бессрочного (неопределенно длительного по времени) обыкновенного аннуитета, тыс. руб.
В практической деятельности коммерческих организаций возможна ситуация, когда поступления денежных средств происходят в начале каждого периода (например, лизинговые платежи).
Последовательность определения будущей стоимости обязательного аннуитета представлена на рис. 4.

Рис. 4. Схема подсчета будущей стоимости обязательного аннуитета
В математическом исчислении показатель будущей стоимости обязательного аннуитета определяется по формуле
FVADn = P*FVIFAr,n*(1+r).
Последовательность нахождения текущей стоимости обязательного аннуитета представлена на рис. 5.
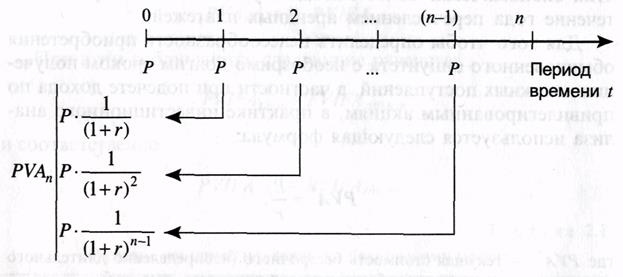
Рис. 5. Последовательность расчета текущей стоимости обязательного аннуитета
В инвестиционной деятельности большинства компаний часто встречаются не эквивалентные между собой денежные потоки (получение дивидендов по обыкновенным акциям, поступление выручки от реализации продукции и пр.). В связи с этим перед финансовыми аналитиками нередко возникает проблема определения временной ценности неравных денежных потоков.
Текущая стоимость всей совокупности будущих денежных потоков равна сумме текущих стоимостей ее индивидуальных компонентов. Согласно этому правилу текущая стоимость поступления неравных денежных потоков за п периодов времени определяется по формуле
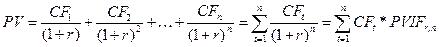
где CFt — денежный поток в период времени t, тыс. руб.
Вышеприведенное выражение называется формулой дисконтированного денежного потока (DCF) и часто используется в финансовых расчетах.
Важным направлением инвестиционного анализа является оценка воздействия инфляции на ход реализации инвестиционных решений и ее взаимодействие с процентными ставками. Агрегированный индекс цен, рассчитываемый через товарообороты всей номенклатуры товаров, определяется по формуле
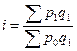
где р1, p0 — соответственно фактическая (прогнозируемая) цена в отчетном периоде и фактическая цена в базисном периоде, тыс. руб.; q1 — объем реализованной продукции по конкретной товарной группе, нат. ед. изм.
Основываясь на определении эффективной годовой процентной ставки (EAR), годовую величину инфляции рассчитываем по формуле
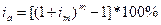
где ia — ожидаемая годовая ставка инфляции, %;
im — ставка инфляции за период (неделю, декаду, месяц и пр.), коэф.
Например, зная величину недельного темпа инфляции (см. российский еженедельник «Эксперт»: раздел «Индикаторы финансового рынка России») за период с 04.05 по 10.05.2000 г., равную 0,4%, можно определить текущую годовую ставку инфляции. Годовая ставка инфляции, рассчитанная по текущим недельным данным о росте цен, составит 23,07% ([1 + 0,004]52 — 1]*100).
В инвестиционном анализе часто используется ожидаемая в будущем инфляционная ставка, при этом рассчитывается ее средняя величина за весь срок реализации инвестиционного проекта (или обращения ценной бумаги). Расчет данного показателя рекомендуется осуществлять с использованием формулы средней геометрической
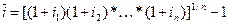
где 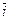 — средняя геометрическая инфляционная ставка за п периодов времени, коэф.
— средняя геометрическая инфляционная ставка за п периодов времени, коэф.
В продолжение обзора показателей, учитывающих временную ценность денежных вложений, необходимо обратить внимание на формулу Фишера, которая объединяет основные финансовые переменные:
- реальную процентную ставку, не содержащую в себе фактор инфляции (r);
- номинальную процентную ставку, рассчитанную с учетом инфляции (rп);
- ожидаемую ставку инфляции (i).
Зависимость между процентными ставками и ожидаемой инфляцией может быть представлена следующим выражением:
(1 + rn) = (1 + r)(1 + i).
Из данной зависимости номинальная процентная ставка рассчитывается по формуле
rn = r + i+r*i.
В условиях низкой инфляции на практике пренебрегают значением r*i, используя при этом упрощенную формулу расчета номинальной процентной ставки rn = r + i.
В качестве информационной базы инвестиционного анализа часто используются исторические данные и материалы, собранные на основе текущей информации. Очевидно, что если базовые переменные в будущих периодах времени изменят свои предполагаемые значения, то соответственно произойдет изменение ожидаемой эффективности инвестиционных операций. Таким образом, можно сделать следующие выводы:
1. Цена заемного капитала уже включает в себя ожидаемую инфляцию.
2. Заемщики капитала будут в наибольшей выгоде, если фактический уровень инфляции больше, чем ожидаемый рост цен, и соответственно планируемая ими эффективность от проведения финансово-инвестиционных операций будет значительно ниже, если фактическая инфляция ниже ее ожидаемого уровня.
3. Величина реальной процентной ставки воздействует на результативность осуществления финансовых операций. Чем выше значение r, тем ниже текущая стоимость получаемых в будущем доходов (процентов, дивидендов и пр.), и наоборот, чем ниже значение r, тем большую ценность имеют будущие результаты с позиции их текущей стоимости.
Процедуры дисконтирования и начисления сложных процентов широко используются в банковских, пенсионных и страховых операциях.
Осуществление инвестиционного анализа неразрывно связано с учетом временных параметров реализации долговременных капиталовложений. В ходе подготовки обобщающих показателей эффективности долгосрочных инвестиций (проекта) процедуры дисконтирования применяются в расчете чистой текущей стоимости (NPV), внутренней нормы рентабельности (IRR), индекса доходности (РI) и др. В связи с этим процедуры анализа проектной дисконтной ставки выступают в качестве базовых мероприятий, осуществление которых во многом предопределяет степень объективности результатов оценки эффективности долгосрочных инвестиций.
Выводы
Временная ценность денежных вложений относится к одной из основных концепций, используемых в инвестиционном анализе. Необходимость учета временного фактора заставляет особое внимание уделять оценке базовых финансовых показателей.
Разность в оценке текущих денежных средств и той же их суммы в будущем может быть вызвана негативным воздействием инфляции, возможностью альтернативного вложения денежных средств, ростом риска, связанного с вероятностью невозврата инвестированных средств, потребительскими предпочтениями.
Нахождение будущей стоимости денежных средств возможно при наличии информации о следующих переменных: сроке вложения (количестве периодов начислени процентов), темпе прироста (процентной ставке), первоначальной величине средств. Нахождение текущей стоимости денежных средств осуществляется аналогично из их будущей стоимости.
Использование простого процента (simple interest) свидетельствует о том, что инвестор будет получать доход (наращивать капитал) только с принципиальной суммы начальных инвестиций в течение всего срока реализации проекта. В противоположность данному подходу использование сложного процента (compound interest) свидетельствует о том, что полученный доход (проценты, дивиденды или пр.) периодически добавляется к сумме начальной инвестиции, в результате помимо первоначальной суммы денежных средств процент берется также из накопленной в предыдущих периодах суммы процентных платежей или любого другого вида доходов.
Аннуитетпредставляет собой равные по величине денежные потоки, возникающие в каждом периоде определенного временного интервала. Примером аннуитета могут служить периодическая выплата процентов по заемным средствам финансирования, купонного дохода по облигациям, перечисление арендной платы и пр. Поступления и выбытия средств могут происходить как в начале (обязательный аннуитет), так и в конце каждого конкретного периода (обыкновенный или отложенный аннуитет). В практике финансовых расчетов наиболее часто используется обыкновенный аннуитет.
Вопросы для самоконтроля
1. Назовите факторы, определяющие разность в оценке текущих денежных средств и их стоимости в будущем.
2. Опишите процедуру наращения денежных потоков. Что означает использование «простого» и «процента» процента.
3. Опишите процедуру дисконтирования денежных потоков. Как изменится алгоритм расчета, если начисления производятся несколько раз в течение года?
4. Приведите пример ситуаций, когда употребляются операции наращения и дисконтирования.
5. В чем смысл расчета показателя эффективной годовой процентной ставки? Как выглядит формула будущей стоимости денежных потоков при непрерывном дисконтировании?
6. Дайте определение аннуитета. Как рассчитывается текущая и будущая стоимость аннуитета?
7. Приведите примеры ситуаций, когда используются текущая и будущая стоимость аннуитета.
8. Что такое формула Фишера?
Дата добавления: 2015-10-19; просмотров: 5550;
