Определение ошибки выборочной доли

При повторном отборе средняя ошибка выборочной доли рассчитывается по формуле:

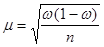
где 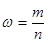- выборочная доля единиц, обладающих изучаемым признаком;

m - число единиц, обладающих изучаемым признаком;

n - численность выборки.

При бесповторном способе отбора средняя ошибка выборочной доли определяется по формуле:

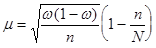
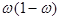- дисперсия выборочной доли

Предельная ошибка выборки 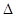связана со средней ошибкой выборки m отношением:

.

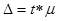При этом t как коэффициент кратности средней ошибки выборки зависит от значения вероятности P, с которой гарантируется величина предельной ошибки выборки.

Предельная ошибка выборки при бесповторном отборе определяется по следующим формулам:

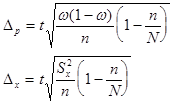
Предельная ошибка выборки при повторном отборе определяется по формуле:

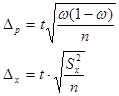
Поскольку величина предельной ошибки выборки 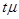, точность оценки параметров генеральной совокупности будет зависеть от принятого уровня доверительной вероятности и от величины стандартной ошибки выборки. Допустим, что доля брака по данным выборки составила 0,02 (или 2%) при n =1000 и N = 10000. Величина стандартной ошибки случайной бесповторной выборки равна 0,0042.

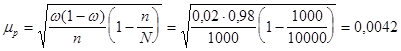(или 0,42%)

С вероятностью 0,954 мы можем утверждать, что предельная ошибка доля брака не превысит 0,0084 ( 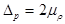) и доля брака в генеральной совокупности будет находиться в интервале: 0,0116 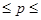0,0284 ( 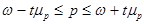). Если мы примем доверительную вероятность равной 0,997, то величина предельной

ошибки выборки составит 0,0126 (0,0042*3), и доля брака в генеральной совокупности будет находиться в интервале 0,02±0,0126, т.е. 0,74% 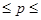3,26%.

Таким образом, с вероятностью 99,7% можно ожидать, что количество бракованных деталей во всей партии из 10000 штук будет находиться в интервале от 74 до 327 штук, тогда как с вероятностью 95,4% доверительный интервал составит 116¸284 штуки. Незначительно увеличивая достоверность выводов (с 95,4 до 99,7%), мы существенно снижаем точность оценки. В этой связи в экономических расчетах чаще рекомендуется использовать доверительную вероятность P=0,95 или 0,954 (соответственно t равно 1,96 и 2,00).