Передаточная функция

Передаточной функцией звена W(S) называется отношение изображений Лапласа выходной и входной величины, полученное при нулевых начальных условиях.

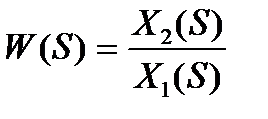
где S – оператор Лапласа

Ее определение дается на базе преобразования Лапласа:

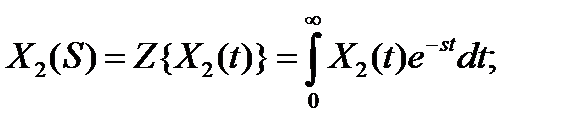
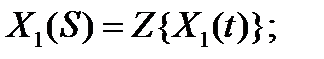
Применив это преобразование к ДУ звена (2.2) записанному в виде:

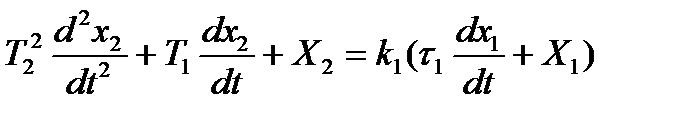
получим

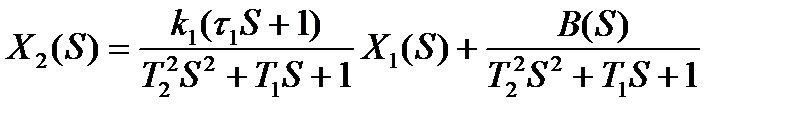
где B(S) – многочлен, включающий в себя все члены с величинами начальных условий.

При нулевых начальных условиях B(S)=0

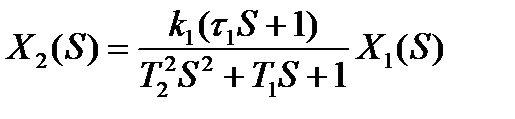
Тогда

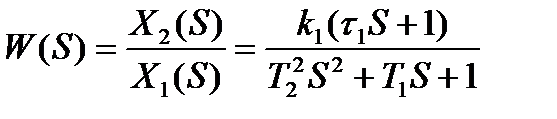- инерционное звено II –го порядка (2.5)

Сравнивая выражение (2.5) с уравнением звена (2.2) видно, что формально передаточную функцию звена можно составить как отношение операторных многочленов правой и левой частей уравнений звена, заменив при этом оператор дифференцирования р на оператор Лапласа S. И наоборот, зная передаточную функцию (2.5), легко написать его уравнение.

В общем случае передаточная функция звена имеет вид

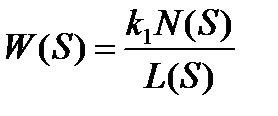(2.6)

где N(S), L(S) – многочлены с коэффициентами 1 в младших членах, причем степень N(S), как правило, ниже степени L(S).

2.На основании (2.6) характеристич. уравнение звена пишется в виде

L(λ)=0,

где λ_i - корни характеристического уравнения звена (полюса передаточной функции).