Метод расчета нормы внутренней доходности

Метод расчета внутренней нормы прибыли. Внутренняя норма прибыли (IRR) – это норма доходности, при которой дисконтированная стоимость притоков наличности (реальных денег) равна дисконтированной стоимость оттоков, то есть такое значение коэффициента дисконтирования, при котором NPV проекта равен нулю (формула 7.19):

IRR = r, при котором NPV = f (r) = 0 (7.19)

где IRR – норма внутренней доходности;

r – средневзвешенная стоимость инвестиционных ресурсов.

Экономический смысл этого показателя заключается в следующем: предприятие может принимать любые решения инвестиционного характера, уровень рентабельности которых не ниже текущего значения показателя CC (или цены источника средств для данного проекта, если он имеет целевой характер). Именно с ним сравнивается показатель IRR, рассчитанный для конкретного проекта, при этом связь между ними такова.

Если IRR > CC - проект подлежит дальнейшей оценке по другим критериям; IRR < CC - однозначно проект отвергается; IRR = CC - проект ни прибыльный, ни убыточный, те. не имеет экономического смысла, возможна реализации в случае целевого финансирования и при условии большой социальной или экологической значимости.

Практическое применение данного метода осложнено, если в распоряжении аналитика нет специализированного программного обеспечения. В этом случае применяется метод последовательных итераций с использованием табулированных значений дисконтирующих множителей. Для этого с помощью таблиц дисконтирующих коэффициентов выбираются два значения коэффициента дисконтирования, таким образом, чтобы в интервале [r ₁, r ₂] функция NPV = f(r) обязательно меняла свое значение с "+" на "–" или с "–" на "+". Далее применим формулу 7.20:

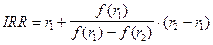, (7.20)

где IRR –норма внутренней доходности;

r₁ - значение коэффициента дисконтирования, при котором f (r₁) > 0 (f (r₁) < 0);

r₂ - значение коэффициента дисконтирования, при котором f (r₂) < 0 (f (r₂) > 0).

Точность вычислений обратно пропорциональна длине интервала [r ₁,r ₂], а наилучшая аппроксимация с использованием табулированных значений достигается в случае, когда длина интервала равна 1 %, т.е. r1 и r2 – ближайшие друг к другу значения коэффициента дисконтирования, удовлетворяющие поставленным условиям (в случае изменения знака функции с "+" на "–"):

r₁ — значение табулированного коэффициента дисконтирования, минимизирующее положительное значение показателя NPV, т.е. f(r₁)=min_r{f(r)>0};

r₂ — значение табулированного коэффициента дисконтирования, максимизирующее отрицательное значение показателя NPV, т.е. f(r₂)=max_r{f(r)<0}.

Путем взаимной замены коэффициентов r₁ и r2 аналогичные условия выписываются для ситуации, когда функция меняет знак с "–" на "+".

Исследуя экономическую эффективность инвестиционных проектов методом внутренней нормы доходности (IRR-метод) как для ординарного, так и для неординарного денежных потоков вытекает, что дисконтированная сумма притока денежных средств равна дисконтированной сумме оттока денежных средств, т.е ∑ DCOF₁ = ∑ DСIF, де в качестве коэффициента дисконтирования выступает ставка внутренней нормы доходности .

Значение MIRR (ставка коэффициента дисконтирования, уравновешивающая притоки и оттоки средств) не во всех случаях является корректным. Использование формулы модифицированной нормы внутренней доходности не уместно, если за основу расчетного коэффициента дисконтирования принята величина банковского процента за кредит.

Расчет MIRR дает более правильную оценку ставки реинвестирования и снимает проблему множественности ставки рентабельности.

Общая формула расчета имеет следующий вид (7.21):

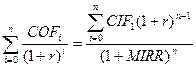, ( 7.21)

где COF₁ - отток денежных средств в i-м периоде (по абсолютной величине);

СIF, - приток денежных средств в i-м периоде;

r - стоимость источника финансирования данного проект;

n - продолжительность проекта.

Если значение MIRR превосходит значение стоимости капитала, проект следует принять. В простейшем случае достаточно рассчитать эти величины для каждого проекта и выбор становится очевиден. Однако, если проектов достаточно много, а также если существуют дополнительные ограничения (например, ограничен спрос на различные виды продукции), то следует построить задачу линейного программирования и решить ее с помощью надстройки «Поиск решения».

Такая задача будет иметь следующий вид: x_i (i =1,n ) – переменная, которая принимает значение 1, если проект выбран для реализации, и 0 – в противном случае.

Целевая функция F=∑NPV_i *x_i - суммарная оценка эффективности инвестиционного портфеля.

Ограничения:

∑I_0i *x_i ≤ R – начальные инвестиции во все выбранные проекты не должны превышать заданной суммы R;

0≤ x_i ≤ 1, x_{i –} целое – условия, вытекающие из смысла переменных.

Если требуют условия осуществления проекта, то могут быть добавлены и другие ограничения.

Методы расчетов показателей для проведения оценки перспективной кредитоспособности при инвестиционном кредитовании, применяемые как в зарубежной, так и в отечественной практике имеют ряд недостатков, нуждаются в совершенствовании и требуют создания современного самообновляемого программного обеспечения, облегчающего создание и экономический анализ эффективности инвестиционных проектов.