Анализ риска и неопределённости

Менеджеру, как правило, приходится принимать реше­ния в условиях неопределенности ряда факторов. Приня­то различать два случая.

1. Когда известна или может быть определенавероятность наступления природного события или действий партнеров. В этом случае говорят о принятии решения в условиях риска.

2. Когда не известнывероятности наступления собы­тий природы или действий партнеров. В этом случае говорят о принятии решения в условиях неопределенности.

Marketing Expert дает возможность пользователю учи­тывать вероятностный характер будущих событий и тем самым проводить анализ риска и неопределенности. Про­грамма позволяет задавать как вероятностный характер факторов микроокружения (доходы от продаж, операци­онные и производственные издержки — диалог «Анализ риска»), так и факторы макроокружения (объем рынка, доля рынка — диалог «Анализ неопределенности»).

Обычно рассматриваемые критерии принятия решения в условиях риска:

- ожидаемое значение;

- комбинация ожидаемого значения и дисперсии;

- предельный уровень;

- наиболее вероятного события в будущем.

Критерий ожидаемого значения - математическое ожидание. Такой подход являет­ся естественным переходом от детерминированных задач к задачам вероятностным.

Использование этого критерия допустимо лишь в том случае, когда одно и то же решение приходится прини­мать многократно.

Действительно, пусть х — случайная величина, харак­теризующаяся математическим ожиданием М(х) и дис­персией D(x). Для случайной выборки объема п выбороч­ное среднее (оценка математического ожидания),в соответствии с предельной теоремой Чебышева при п 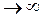стремится к веро
ятностной характеристике МО.

Критерий ожидаемого значения — дисперсия. Может использоваться, когда ситуация повторяется нечасто. При уменьшении дисперсий среднее значение также стремится к математическому ожиданию. Отсюда возможным крите­рием, учитывающим дисперсию можно принять

М(х) + kD(x) —> min или М(х) — kD(x) —> max

Здесь k — заданная постоянная, которую иногда интер­претируют как уровень несклонности к риску. Действи­тельно, этот коэффициент определяет степень важности дисперсии по отношению к МО.

Критерий предельного уровня.

Критерий предельного уровня не дает оптимального решения, максимизирующе­го, например, прибыль. Скорее, он соответствует опреде­лению приемлемого способа действий. Например, риэлтер­ская фирма должна быстро оценить предлагаемую на про­дажу квартиру. Эксперт устанавливает предельно низкую цену, по которой она может быть продана и, вычтя нало­ги и минимальный процент, устанавливает цену покупки. Конечно, это не оптимальное решение, т.к. кто-то может предложить фирме квартиру дешевле. Тем не менее, такой подход позволяет принимать решение и в том случае, ког­да нет достаточно полных сведений о ситуации на рынке. В рассматриваемом примере нет упоминания о вероятнос­ти, фактически риэлтер учитывает плотность вероятности интуитивно.

Критерий наиболее вероятного исхода.

Если одно из значений случайной величины имеет вероятность, зна­чительно превышающую вероятности других значений, то часто такую случайную величину заменяют ее наибо­лее вероятным значением. Пример: приобретая билет на самолет, большинство пассажиров исходит из того, что самолет долетит до пункта назначения, хотя суще­ствует вероятность (пусть небольшая), что этого не про­изойдет.