Тема 2.1.7 Реальный газ. Уравнение состояния реального газа.

План

1. Реальный газ.

2. Уравнение состояния реального газа.

Литература:

[1] Чолпан П.П. Фізика: Підручник. – К.: Вища к.., 2004. –119с. (§ 4.9 )

1 Опыт свидетельствует, что законы, характеризующие идеальный газ, в первом приближении можно применять к разреженным реальным газам. Для реальных газов с умеренной и большой плотностью отклонения от законов идеального газа значительны.

Для многих реальных газов взаимная потенциальная энергия частиц изменяется зависимо от расстояния между ними по закону Леннарда-Джонса:

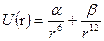
где первый член учитывает притяжение между частицами, а второй — отталкивание между ними.

Силы притяжения между частицами реального газа называют вандерваальсовыми силами по имени голландского физика Й. Ван дер Ваальса (1837—1923), который их открыл. Теорию вандерваальсовых сил притяжения разработал П. Дебай для газов, молекулы которых имеют постоянный дипольный момент, В. Кеезом — для газов, в которых лишь часть молекул характеризуется постоянным дипольным моментом, и Ф. Лондон — для газов з к. альніенн молекулами.

Хотя сейчас известно свыше 150 уравнений состояния реальных газов, найденных эмпирически и теоретически, уравнения состояния реального газа Ван дер Ваальса (1873 г.) не утратило своего научного значения. Это объясняется прежде всего тем, что оно теоретически обоснованно и имеет сравнительно простой вид. Для моля реального газа

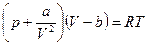
где а/V² — поправка на силы притяжения между молекулами, или так называемое внутреннее давление газа; b — поправка на собственный объем молекул. Важным результатом уравнения Ван дер Ваальса является то, что оно допускает непрерывный переход между жидким и газообразным состояниями. Сравнивая теоретические изотермы Ван дер Ваальса с экспериментальными изотермами Эндрюса для СО, пришли к более глубокому пониманию физического содержания как отдельных участков изотерм, которые отвечают одно- и двухфазовым состояниям, так и критического состояния вещества.

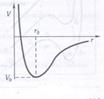
2 На рис. изображены изотермы Ван дер Ваальса для разных температур (Т₁ < Т₂ < Т₃ < Т₄). На этих изотермах наблюдается s-образный участок, который тем больше, чем ниже температура, которой соответствует изотерма. Чтобы теория Ван дер Ваальса по крайней мере качественно объясняла фазовые переходы, ее формально дополняют правилом Максвелла. Согласно с этим правилом горизонтальные прямые (штриховая линия АО) проводят так, чтобы площади s₁ и s₂, отсекаемые этой прямой и изотермой Ван дер Ваальса, были одинаковы. Изотермы с горизонтальным участком совпадают с экспериментальными изотермами Эндрюса. Рассмотрим внимательнее изотермы Ван дер Ваальса на примере изотермы, соответствующей температуре Т₁. Отрезок G^/G отвечает газообразному состоянию. GА — двухфазному состоянию жидкость — пар,

АА’ — жидкому состоянию, Gg — переохлажденному пару, а аА — перегретой жидкости. Отрезок ga практически реализовать невозможно, поскольку для состояний, соответствующих этому отрезку, с увеличением объема должно возрастать и давление, то есть 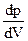> 0, что противоречит условию стабильного состояния. Кривую АВСDЕFG называют бинодалью. Она отделяет геометрическое место точек, соответствующих двухфазным и метастабильным однофазным состояниям. Вершина этой кривой совпадает с критической точкой D, а критическая изотерма, в отличие от других изотерм, имеет лишь точку перегиба. Для критической точки

и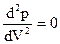

Тогда из уравнения Ван дер Ваальса несложно получить значения критических параметров через постоянные а и b:

Заметим, что хотя уравнение Ван дер Ваальса и правильно передает основные закономерности поведения реальных газов, но количественные результаты, полученные с помощью этого уравнения, не всегда удовлетворительны Поэтому возникла потребность поиска других, более точных уравнений состояния.

Одной из причин несовершенства уравнения Ван дер Ваальса является то, что в этом уравнении не берется во внимание возможность ассоциации молекул то есть образование групп. Современные экспериментальные и теоретические исследования свидетельствуют о том, что в газах, даже при высоких температурах, молекулы образуют группы из двух, трех, четырех и более молекул. Чем ниже температура, тем больше многоатомных молекулярных комплексов, тем прочнее связь между молекулами в группе. При определенных условиях начинается процесс интенсивного группообразования — процесс конденсации.

Теория реальных газов приобрела заметное развитие вследствие применения новых статистических методов, предложенных М. Боголюбовым, Р. Майером и другими учеными.

Уравнение состояния реальных газов, выведенное статистическими методами, имеет такой вид:

где Вn — віріальні коэффициенты, которые можно рассчитать, если известен характер взаимодействия между молекулами.

Контрольные вопросы

1 Почему в молекулярной физике преимущество отдают статистическому методу исследования?

2 Какие существуют агрегатные состояния вещества?

3 Какие силы называют вандерваальсовыми силами?

4 Проанализируйте уравнение Ван дер Ваальса и его изотермы.

Содержательный модуль 2.2 Законы термодинамики