Тема 2.1.3 Распределение Максвелла молекул идеального газа по скоростям теплового двиения.

План

1 Распределение молекул по скоростям теплового движения.

2 Кривая распределения скоростей молекул, ее характеристика. Формула закона распределения Максвелла.

3 Наиболее характерные скорости.

Литература:

[1] Чолпан П.П. Фізика: Підручник. – К.: Вища к.., 2004. – 567 с.

(§ 4.7 )

[2] За редакцією І.Є. Лопатинського. Зачек І.Р., Кравчук І.М., Романишин Б.М. та к.. Курс фізики:

Навчальний підручник. – Львів: Видавництво «Бескид Біт», 2002 р. – 367 с. (§ 31)

1В равновесном состоянии параметры газа остаются неизменными, но микросостояния – взаимное расположение молекул, их скорости – непрерывно изменяются.

Поскольку все направления движения равно вероятны, распределение молекул по направлению будет равномерным. Скорости молекул составляют от нуля до бесконечности. Эти значения не являются к. альніення.

Скорости молекул группируются в основном около некоторого наиболее вероятного значения.

Итак, распределение молекул по скоростям не произвольно и должно подчиняться определенному закону. Этот закон касается не каждой данной молекулы, а всей совокупности молекул, то есть он является статистическим. Закон распределения молекул по скоростям установил Дж. Максвелл в 1869 г. Обоснованию и установлению границ применения его посвящены научные труды российского физика М. М. Пирогова.

Распределение молекул по скоростям изображено на рисунке. По оси абсцисс отложены значения скорости отдельных молекул газа. Если υ и υ + dυ – достаточно близкие значения скорости, а 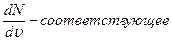среднее значение ординаты, то 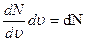(площадь элементарной полосы под кривой) является числом молекул, скорость которых лежит в пределах от υ до υ + dυ. Тогда площадь под кривой будет равна общему числу молекул исследуемого газа N. Считают также, что все молекулы этого газа одинаковы и температура во всех частях газа одна.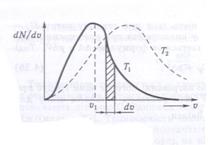

2 Рассматривая кривые распределения скоростей молекул, можно отметить такие особенности их:

1 Кривая распределения скоростей молекул газа проходит через начало координат. Итак, нет молекул, которые бы не двигались.

2 Кривая имеет максимум, после которого асимптотически приближается к оси абсцисс. Итак, очень большие скорости маловероятны. Это возможно только при условии, что молекула при многих столкновения с другими молекулами будет получать энергию, а не отдавать ее, что является невероятным.

3 Кривая распределения скоростей несимметрична – с одной стороны спад кривой более крутой, чем с другой.

Закон распределения Максвелла можно записать так:

,
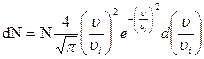где N – общее число молекул в заданной массе газа; dN – число молекул, скорости которых лежат в пределах от υ до υ + dυ; υ_і – наиболее вероятная скорость.

3 Скорость υ_і, которая отвечает максимуму кривой распределения скоростей молекул, называется наиболее вероятной скоростью. Согласно с теорией Максвелла наиболее вероятную скорость можно определить формулой

,

где R – универсальная газовая постоянная; Т – абсолютная температура; μ – молярная масса.

Средняя квадратичная скорость определяется так:

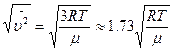
Среднюю арифметическую скорость, согласно теории, можно вычислить по формуле:

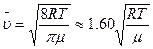
Контрольные вопросы

1 Проанализируйте распределение молекул газа по скоростям (закон Максвелла)

2 Как изменяется вид кривой распределения, если температура повышается?

3 Что такое наиболее вероятная скорость?

4 Назовите особенности кривых распределения скоростей молекул.

5 Определите среднюю арифметическую, среднюю квадратичную и наиболее вероятную скорости молекул газа плотностью 0,3г/л при давлении 300мм.рт. ст.

Содержательный модуль 2.1 Законы идеального газа

Тема 2.1.4 Экспериментальная проверка закона распределения Максвелла.(Самостоятельное изучение)

План

1 Средняя скорость теплового движения молекул.

2 Экспериментальное определение скоростей молекул.

3 Уравнения состояния идеального газа.

Литература: [3] Дмитрієва В.Ф. Фізика: Навчальний посібник для студентів навчальних закладів І-ІІ рівнів акредитації. – К: Техніка, 2008. – 648 с. (§ 40)

1 Уравнение 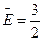kТ дает возможность найти средний квадрат скорости движения молекулы. Подставив в это уравнение 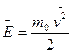, получим выражение для среднего квадрата скорости: .

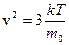Квадратный корень из этой величины называется средней квадратичной скоростью.

Рассчитывая скорость молекул, например, азота при t=0⁰С, получим 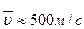. Молекулы водорода при той же температуре имеют среднюю скорость υ≈1800 м/с.

Когда впервые были получены эти числа (вторая половина ХІХ в.) много физиков были озадачены. Скорости молекул газа по расчетам оказались большими, чем скорость пушечных снарядов! Высказывались на этом основании даже сомнения в справедливости кинетической теории. Известно, что запахи распространяются достаточно медленно: нужно время порядка десятка секунд, чтобы запах духов, которые разлили в одном углу комнаты, распространились до другого угла (за счет конвекции это время может уменьшиться до 1 с). Это легко объяснить. Из-за столкновения молекул траектория каждой молекулы представляет собой запутанную ломаную линию. Большие скорости молекула имеет на прямолинейных отрезках ломаной. Перемещение молекулы в каком-то направлении в среднем невелико даже за время порядка нескольких минут. При перемещении молекулы из точки А в точку В пройденный ей путь оказывается большим, чем расстояние АВ.

2Опыты по определению скоростей молекул доказали справедливость формулы 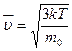. Один из опытов был предложен О. Штерном в 1920 г.

Прибор Штерна состоит из двух коаксиальных цилиндров А и В, жестко связанных друг с другом. Цилиндры могут вращаться с постоянной угловой скоростью. Вдоль оси малого цилиндра натянут тонкий платиновый проводок С, покрытый слоем серебра. По проводу пропускают электрический ток. В стенке этого цилиндра есть узкая щель О. Кислород из цилиндров откачали. Цилиндр В находится при комнатной температуре.

Сначала прибор неподвижен. При прохождении тока по нити слой серебра испаряется, и внутренний цилиндр заполняется газом из атомов серебра. Некоторые атомы пролетают через щель О и достигают внутренней поверхности цилиндра В, оседают на нее. В результате прямо напротив щели образуется узкая полоса серебра Д.

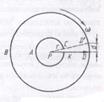Потом цилиндр приводят в движение с большим числом оборотов n в секунду (до 1500 1/с). Теперь за время t, необходимое атому для прохождения пути, равного разности радиусов цилиндров R_В – R_А, цилиндры повернутся на некоторый угол φ. В результате атомы, которые движутся с постоянной скоростью, попадают на внутреннюю поверхность большого цилиндра не прямо напротив щели О, а на некотором расстоянии s от конца радиуса, который проходит через середину щели; т.е. атомы движутся прямолинейно.

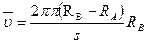
Модули скоростей, определенные из опыта, совпадают с теоретическим значением средней квадратичной скорости. Это служит экспериментальным доказательством справедливости формулы.

3 На основании зависимости р = nkT можно получить уравнение, связывающее все три макроскопических параметра p, V, T, которое характеризует состояние данной массы достаточно разреженного газа. Это уравнение называют уравнением состояния идеального газа.

Подставим в уравнение р = nkT выражение для концентрации молекул газа. Концентрацию газа можно записать так n = N/V=1/V*m/M*N_A,

где N_A – постоянная Авогадро, m – масса газа, М – его молярная масса. После подстановки получим pV=m/MkN_AT.

Произведение постоянной Больцмана k и постоянной Авогадро N_A называют универсальной (молярной) газовой постоянной и обозначают буквой R.

Подставив в уравнение pV=m/MkN_AT вместо kN_A универсальную газовую постоянную R, получим уравнение состояния для произвольной массы идеального газа:

pV=m/MRT.

Единственная величина в этом уравнении, которая зависит от рода газа – это его молярная масса.

Из уравнения состояния вытекает связь между давлением, объемом и температурой идеального газа, который может находиться в любом из двух состояний.

Контрольные вопросы

1 Сформулируйте основные положения МКТ.

2 Что такое молекула?

3 Что такое атом?

4 Что называется количеством вещества?

5 Цель опыта Штерна.

6 Результаты опыта, их объяснение.

Содержательный модуль 2.1 Законы идеального газа

Тема 2.1.5 Агрегатные состояния и фазовые превращения вещества.(Самостоятельное изучение)

План

1 Определение строения тел и характера молекулярного движения.

2 Строение и характер молекулярного движения газов и кристаллов.

3 Закон Авогадро. Закон Дальтона.

Литература

[1] Чолпан П.П. Фізика: Підручник. – К.: Вища шк.., 2004. – 567 с. (§ 4.2 )

1 Вещество зависимо от термодинамических параметров – давления, объема и температуры – может пребывать в трех агрегатных состояниях: твердом, жидком и газообразном. Кроме того, вещество при определенных условиях может быть в состоянии плазмы. Современные агрегатные состояния немного напоминают четыре стихии древних: Земля – твердое состояние, вода – жидкое состояние, воздух – газообразное состояние, огонь – плазму.

Строение тел и характер молекулярного движения определяются силами взаимодействия между молекулами, а силы взаимодействия тем меньше, чем больше межмолекулярные расстояния. В газах среднее расстояние между молекулами достаточно велико сравнительно с размерами молекулы. Молекулы движутся хаотично, изменяя направление движения при столкновениях друг с другом или со стенками сосуда, но между столкновениями молекулы движутся практически независимо друг от друга, поскольку силы взаимодействия малы. В твердых кристаллических телах расстояния между молекулами значительно меньше, чем в газах, а потому межмолекулярные силы больше. Из-за этого молекулярное движение в кристаллах имеет совсем другой характер, чем в газах. В кристаллах молекулы, атомы или ионы (зависимо от рода вещества) переходят с места на место сравнительно редко, большую часть времени они пребывают в колебательном движении относительно некоторых неподвижных точек, или узлов, которые являются положениями равновесия. Эти узлы распределяются в пространстве зависимо от характера межмолекулярного взаимодействия. Повышение температуры твердого тела приводит к увеличению амплитуды колебаний молекул, расстояний между узлами (расширение тела от нагревания) и, значит, к ослаблению сил сцепления. От этого атомы чаще оставляют свои узлы, а при определенной температуре, которая называется температурой плавления, исчезает упорядоченность в расположении центров колебаний, решетки разрушаются, и происходит переход в жидкое состояние.

2 Газы и кристаллы различаются строением и характером молекулярного движения. Газы характеризуются хаотичностью, кристаллы — упорядоченностью в расположении молекул. В этом понимании газы и кристаллы имеют противоположные свойства. В жидкостях диалектично объединяются эти противоположные свойства. Молекулы газов движутся поступательно, а молекулы кристаллов колеблются вокруг неподвижных положений равновесия. Молекулы жидкостей колеблются подобно молекулам кристаллов, но положения равновесия, относительно которых происходят колебания, не остаются неподвижными, как в кристаллах, а время от времени смещаются. В жидкости выступают в единстве порядок, характерный для кристаллов, и беспорядок, характерный для газов. Молекулы жидкости не так прочно связаны друг с другом, как молекулы твердых тел. Но взаимодействие между ними значительно больше, чем в газообразном состоянии. Молекулы жидкости могут преодолеть эти силы связи. При определенной температуре молекулы жидкости имеют резкую скорость и та или иная молекула может приобрести достаточную энергию для преодоления сил связи. Если движение молекулы направлено к поверхности жидкости, то она может выйти из нее. Этот процесс называется испарением. Он может происходить при любой температуре. Такие рассуждения можно применить также для твердого тела, чтобы объяснить возможность испарения твердых тел без предварительного превращения в жидкость. Это явление называют сублимацией.

Плотность газа при нормальных условиях значительно меньше, чем плотность того же вещества в жидком состоянии: р_р – 1000 р_г. Связь расстояний между частицами для газа и жидкости такая: 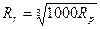. Длина свободного пробега молекул в газообразном состоянии λ≈10^{-7 м. средняя скорость движения молекул газа при комнатной температуре 400…500 м/с. Размеры одного атома около 10-10 м, молекулы — 3 * 10-10 м. Средняя плотность атомов в Солнечной системе составляет 109} атомов/м³, в Галактике — 10⁶ атомов/м³, вне Галактики — 10⁵…10⁶ атомов/м³.

3По закону Авогадро, если какие-либо два газа занимают одинаковые объемы при одинаковом давлении и имеют одинаковые температуры, то в этих объемах содержится одинаковое число молекул. Из этого закона вытекает, что моли каких-либо веществ в газообразном состоянии при одинаковых давлениях и одинаковых температурах занимают одинаковые объемы. Число молекул в моле любого вещества N_A = 6,02*10²³ моль^-1. Это число называется числом Авогадро. Опыт свидетельствует, что моль любого вещества в газообразном состоянии при нормальных условиях занимает объем 22,4•10^-3м³. Отсюда можно определить число молекул газа, которое содержится при нормальных условиях в 1 см³. Это число называется числом Лошмидта и равно 2,7*10¹⁹ см^-3.

4 Закон Дальтона для смеси газов формулируется так: давление смеси газов равно сумме парциальных давлений газов, которые образуют смесь. Парциальным давлением называется давление, которое имел бы газ, когда бы он один заполнял весь объем.

Контрольные вопросы и задачи

1 В каких агрегатных состояниях может пребывать вещество?

2 Чем определяются строение тел и характер молекулярного движения?

3 Что такое испарение?

4 Какое явление называют сублимацией?

5 Что утверждает закон Авогадро?

6 Путем испарения 240г аммиака 0,6л воды при 18°С превратилось в лед. Определите К.П.Д. установки.

Содержательный модуль 2.1 Законы идеального газа