Определение элементов внешнего ориентирования снимка по опорным точкам (обратная фотограмметрическая засечка)

Опорной точкой будем называть точку, опознанную на местности и на снимке, геодезические координаты которой на местности известны.

Для определения элементов внешнего ориентирования снимка воспользуемся уравнениями коллинеарности (1.3.12), которые представим в виде

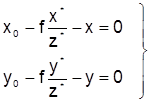; (1.5.1)

где

;

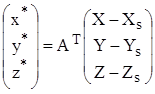или

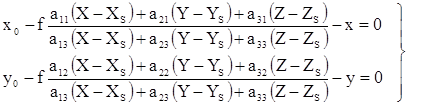. (1.5.2)

Если на снимке измерены координаты изображений опорных точек, то каждая опорная точка позволяет составить 2 уравнения (1.5.2), в которых известны значения координат х,у изображения опорной точки в системе координат снимка Sxyz, геодезические координаты опорной точки в системе координат объекта OXYZ и элементы внутреннего ориентирования снимка f,x₀,y₀.

Неизвестными величинами в уравнениях (1.5.2) являются 6 элементов внешнего ориентирования снимка Xs, Ys, Zs, w, a, À.

Следовательно, для определения 6 неизвестных элементов внешнего ориентирования снимка достаточно иметь не менее 3 опорных точек. При этом опорные точки на местности не должны располагаться на одной прямой. Если имеются 3 опорные точки, координаты изображений которых на снимке измерены, можно составить систему из 6 уравнений (1.5.2) с 6 неизвестными. В результате решения этой системы уравнений можно найти значения элементов внешнего ориентирования снимка.

В связи с тем, что уравнения (1.5.2) нелинейные, решение системы уравнений непосредственно достаточно сложно, поэтому систему уравнений (1.5.2) решают методом приближений.

Для этого уравнения (1.5.2) приводят к линейному виду, раскладывая их в ряд Тейлора с сохранением членов только первого порядка малости, и переходят к уравнениям поправок.

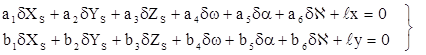. (1.5.3)

В уравнениях (1.5.3):

dXs, … ,dÀ - поправки к приближенным значениям неизвестных элементов внешнего ориентирования снимка Xs⁰,…,À⁰;

a_i, b_i – частные производные от уравнений (1.5.2) по соответствующим аргументам (например, коэффициент а₄ является частной производной от первого уравнения (1.5.2) по аргументу w,то есть );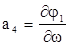

ℓх, ℓу – свободные члены.

Значения коэффициентов уравнений (1.5.3) a_i, b_i вычисляются по известным значениям координат точек снимка и местности х,у и X,Y,Z, известным значениям элементов внутреннего ориентирования снимка f,x₀,y₀ и приближенным значениям неизвестных Xs⁰,…,À⁰.

Свободные члены ℓх, ℓу вычисляются по формулам (1.5.2) таким же образом.

В результате решения системы уравнений поправок (1.5.3) находят поправки к приближенным значениям неизвестных и вычисляют уточненные значения неизвестных.

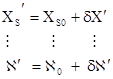
По уточненным значениям неизвестных повторно составляют уравнения поправок (1.5.3) и решают полученную систему уравнений.

Решения повторяют до тех пор, пока величины поправок, найденные в результате решения, не станут пренебрежимо малыми.

В случае если на снимке измерено более трех изображений опорных точек, то для каждой точки составляют уравнения поправок вида:

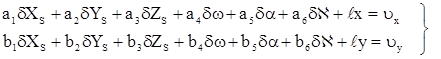; (1.5.4)

Решение полученной системы уравнений (1.5.4) производят методом приближений, по методу наименьших квадратов (под условием V^TV = min).