Метод Рунге-Кутта для уравнений первого порядка

Рассмотрим задачу Коши для дифференциального уравнения.

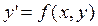
с начальным условием .

Обозначим через 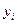приближенное значение искомого решения в точке 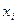. По методу Рунге-Кутта вычисление приближенного значения 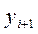в следующей точке 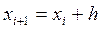производится по формулам

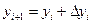
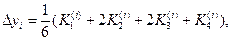
где

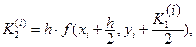
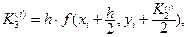
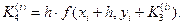
Для записи вычислений используется таблица Правило 4-го порядка точности.

Таблица 9.1.

Шаблон для вычисления решения уравнения (9.6) по методу Рунге-Кутта.

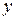
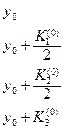
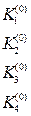
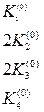
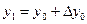
Пример 9.6. Используя метод Рунге–Кутта составить таблицу приближенных значений интеграла дифференциального уравнения 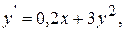удовлетворяющего начальным условиям y(0)=0.2 на отрезке [0;0.5] с шагом h=0.1. Все вычисления будем вести с четырьмя десятичными знаками, расположим их в таблице.

Таблица 9.2.

Решение примера методом Рунге-Кутта.

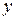
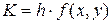
	0,05 0,05 0,1	0,2 0,206 0,2069 0,2138	0,012 0,0137 0,0138 0,0157	0,012 0,0274 0,0276 0,0157
				0,0138
	0,1 0,15 0,15 0,2	0,2138 0,2217 0,2227 0,2317	0,0157 0,0177 0,0179 0,0201	0,0157 0,0354 0,0358 0,0201
				0,0178
	0,2 0,25 0,25 0,3	0,2317 0,2417 0,2429 0,2544	0,0201 0,0225 0,0227 0,0254	0,0201 0,0250 0,0454 0,0254
				0,0227
	0,3 0,35 0,35 0,4	0,2544 0,267 0,2685 0,2829	0,0254 0,0284 0,0286 0,032	0,0254 0,0568 0,0572 0,032
				0,0286
	0,4 0,45 0,45 0,5	0,2829 0,2989 0,3008 0,3190	0,032 0,0358 0,0361 0,0405	0,032 0,0716 0,0722 0,0405
				0,0360
	0,5	0,3189

При решении задачи Коши для системы дифференциальных уравнений методом Рунге-Кутта

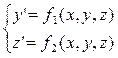
применим формулы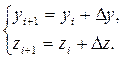

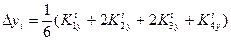
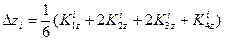
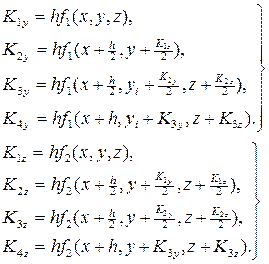
Для контроля правильности выбора шага h рекомендуется вычислять дробь 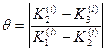. Величина q не должна превышать нескольких сотых. В противном случае шаг следует уменьшить.

Для определения точности пользуются двойным пересчетом.

,

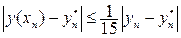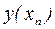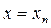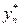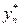где - точное решение уравнения (9.6) в точке , а y_n и приближенные значения, полученные при расчете с шагом h и с шагом , соответственно. Если y_n и мало различимы, то шаг выбран оптимально.

Для решения обыкновенных дифференциальных уравнений и систем в Mathcad предназначено несколько стандартных функций. В частности, для реализации метода Рунге-Кутта четвертого порядка существует функция rkfixed(y,a,b,n,D).

Параметры этой функции:

y-вектор начальных значений,

а,b- начало и конец промежутка интегрирования,

n-число интервалов, на которое делится промежуток интегрирования,

D-вектор правых частей системы обыкновенных дифференциальных уравнений.

Применим данную функцию к решению примера 9.6.

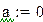
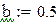
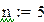
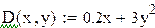
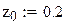
Рис 9.2 Решение примера 9.5 в Mathcad

Пример 9.6. Решим систему обыкновенных дифференциальных уравнений первого порядка с начальными условиями y(0)=2 , z(0)=-1

с помощью этой же стандартной функции на отрезке [0;0.5] с шагом h=0.1

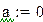
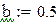
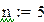
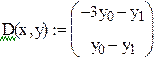
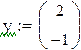
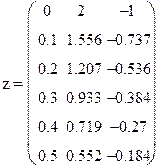
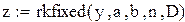
Рис 9.3. Решение примера 9.6 в Mathcad

Первый столбец таблицы это значения переменной x, второй столбец таблицы значения у, а третий столбец значения z в точках от ноля до 0,5 с шагом 0,1.

Пример 9.7. Решить задачу Коши для о.д.у. y"+3y'-xy-x³=5 y(0)=1 y'(0)=2 на отрезке [0;0.5] с шагом h=0.1

Решение уравнения более высокого порядка находится сведением уравнения к системе уравнений первого порядка и применением стандартной функции маткада rkfixed.

После замены переменных получаем систему

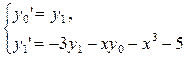
С начальными условиями y₀(0)=1 y₁(0)=2

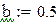
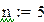
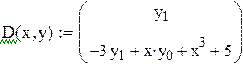
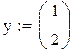
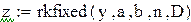
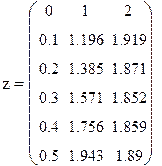
Решение уравнения- второй столбец таблицы.

Рис 9.4. Решение примера 9.7 в Mathcad

ВОПРОСЫ

Вопросы к главе 1

1. Дана функция 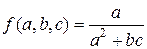. Значения переменных: a = 0.0125,

b = 0.283, c = 0.0187, указаны со всеми верными цифрами в широком смысле этого слова. Оценить погрешность результата, используя оценки погрешностей для арифметических операций.

2. Приведите несколько примеров чисел, с различным количеством десятичных знаков, но с пятью значащими цифрами.

3. Что может являться источником неустранимой погрешности при решении вычислительных задач?

4. Какие источники возникновения погрешностей результата при вычислениях вы знаете?

5. На какую погрешность влияет форма представления числа в компьютере?

6. Дайте определение абсолютной и относительной погрешности.

Вопросы к главе 2

1. Перечислите методы решения трансцендентных уравнений, с которыми вы познакомились в этой главе. Какой из них сходится быстрее всех, какой медленнее всех?

2. Прочитайте и изучите самостоятельно по дополнительной литературе комбинированный метод хорд и касательных.

3. Составьте блок-схему (алгоритм) для метода половинного деления.

4. Пусть в методе половинного деления промежуток, где отделен корень, имеет длину 1. Сколько надо сделать приближений, чтобы ответ получить с точностью 0.0005

5. Как преобразовать уравнение, заданное в виде f(x)=0 к виду, удобному для итераций. Сколькими способами можно это сделать?

6. Сравните метод касательных и его модификации.

7. Будет ли сходиться метод итераций для уравнения

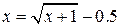
На промежутке (0,5;1)

Вопросы к главе 3

1. Суть метода последовательных приближений для системы линейных алгебраических уравнений?

2. 2. Сформулируйте достаточный признак сходимости для метода итераций, используя понятие нормы матрицы.

3. Приведите пример системы трех линейных уравнений с тремя неизвестными, которая после пребразования к виду удобному для итераций по формулам (3.3), будет сходиться по этому методу.

4. Что общего и в чем отличаются метод итераций и метод Зейделя.

5. Сформулируйте что называется невязкой в методе релаксаций?

6. Условия сходимости метода релаксаций?

7. Как выбрать начальное условие для метода последовательных приближений?

Вопросы к главе 4

1. По каким формулам находятся корни системы из двух нелинейных уравнений методом Ньютона?

2. Как определяются начальные приближения для переменных в методе Ньютона и в методе итераций для систем из двух нелинейных уравнений.

3. Что такое якобиан и какое условие накладывается на его величину в методе Ньютона?

4. Какое условие является достаточным для сходимости метода итераций?

5. Запишите метод итераций в векторном виде.

Вопросы к главе 5

1. Как составляется диагональная таблица конечных разностей?

2. Общая постановка задачи интерполяции.

3. Почему в качестве интерполирующей функции удобно выбрать полином?

4 Составьте интерполяционный многочлен Лагранжа, проходящий через точки с координатами (a,y₀), (b,y₁) , (c,y₂)

5. В каком случае целесообразно пользоваться схемой Эйткена.

6. Как решается задача обратного интерполирования для случая равноотстоящих узлов?

7. Как выбрать количество слагаемых в интерполяционном многочлене Ньютона, если в заданной таблице функции имеется неограниченное число точек?

8. В каких случаях применяют первую интерполяционную формулу Ньютона, а в каких вторую интерполяционную формулу Ньютона.

9. Остаточный член первой интерполяционной формулы Ньютона.

Вопросы к главе 6

1. Что такое сплайновая аппроксимация?

2. Каким четырем условиям должна удовлетворять функция g(x), заменяющая функцию внутри каждого элементарного отрезка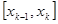

3. Каково происхождение слова сплайн?

4. Дайте определение кубического сплайна.

5 Что такое дефект сплайна?

Вопросы к главе 7

1. Какие методы аппроксимации линейной функцией вы знаете?

2. В чем суть метода наименьших квадратов?

3. Для какого класса аппроксимирующих функций задача нахождения коэффициентов нормальной системы в методе наименьших квадратов имеет единственное решение?

4. Какие значения параметров эмпирической формулы считаются наилучшими в методе наименьших квадратов?

5. Метод выравнивания.

6. Как решается задача аппроксимации многочленами в Маткаде?

7. Аппроксимировать методом наименьших квадратов функцию f(x), заданную таблицей.

8. Как выбрать эмпирическую формулу?

Вопросы к главе 8

1. Какую приближенную квадратурную формулу мы получим, если заменим подынтегральную функцию f(x) на интерполяционный многочлен Лагранжа первого порядка?

2. Какой из методов приближенного вычисления интегралов дает самый точный результат при разбиении промежутка интегрирования на одинаковое число частей?

3. Как выбрать оптимальный шаг интегрирования в методе Симпсона по оценке остаточного члена?

4. В чем суть двойного пересчета?

5. Какую замену переменных надо сделать для вычисления интеграла методом Гаусса на промежутке (a,b)

6. Вычислить интеграл 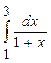по формуле Чебышева для n=4

7. Выведите квадратурную формулу Ньютона (правило3/8)

Вопросы к главе 9

1. Как можно классифицировать приближенные методы решения задачи Коши для обыкновенных дифференциальных уравнений (ОДУ)?

2. Какие методы решения ОДУ называются аналитическими?

3. Сформулируйте условия сходимости метода последовательных приближений.

4. Решить задачу Коши для ОДУ

методом последовательного дифференцирования

Ограничиться 5 членами разложения.

5. Покажите на примере как привести дифференциальное уравнение n-го порядка к системе дифференциальных уравнений первого порядка.

6. Сравните между собой численные методы решения ОДУ, приведенные в главе. Для какого из них для получения одной и той же заданной точности шаг интегрирования будет самый большой, самый маленький?

7. Нарисуйте блок-схему (напишите алгоритм) решения задачи Коши ОДУ первого порядка для одного из улучшенных методов Эйлера.

8. Как составляется таблица для решения задачи Коши дифференциального уравнения первого порядка методом Рунге-Кутта?

9. Опишите встроенную функцию Маткада для решения систем ОДУ первого порядка методом Рунге-Кутта.

Список литературы

1. Демидович, Б.П. Основы вычислительной математики [Текст]: учеб. Пособие для студентов вузов/ Б.П. Демидович, И.А Марон. - Санкт-Петербург: Лань, 2009. - 672 с.

2. Копченова, Н. В. Вычислительная математика в примерах и задачах [Текст]: учеб. Пособие для студентов вузов/ Н. В. Копченова, И.А. Марон. - Санкт-Петербург: Лань, 2008. - 368 с.

3. Демидович, Б.П. Численные методы анализа. Приближение функций, дифференциальные и интегральные уравнения [Текст]: учеб. Пособие для студентов вузов/ Б.П. Демидович, И.А Марон, Э.З. Шувалова. - Санкт-Петербург: Лань, 2010. - 400 с.

4. Бахвалов, Н.С. Численные методы [Текст]: учеб. Пособие для студентов вузов/ Н.С. Бахвалов, Н.П., Жидков, Г.М. Кобельков. М: Бином, 2003. - 632 с.

5. Поршнев, С.В. Численные методы на базе Mathcad [Текст]: учеб. Пособие для студентов вузов/ С.В. Поршнев, И.В. Беленкова.- Санкт-Петербург: БХВ-Петербург, 2005. - 464 с.

6. Кирьянов, Д. В. MathCAD 14[Текст]:/Д.В. Кирьянов - Санкт-Петербург: БХВ-Петербург, 2007. - 704 с.

Оглавление

Введение. 3

Глава 1. Погрешность результата численного решения задачи. 5

1.1. Источники и классификация погрешностей. 5

1.2. Абсолютная и относительная погрешности. Формы записи данных. 6

1.3. Вычислительная погрешность. 9

Глава 2. Решение нелинейных уравнений. 11

2.1. Отделение корней уравнения. 11

2.1.1. Аналитический метод отделения корней. 11

2.1.2. Графический метод отделения корней. 12

2.2. Уточнение приближенных корней. 13

2.2.1. Метод половинного деления. 13

2.2.2 Метод хорд. 15

2.2.3. Метод Ньютона – метод касательных. 19

2.2.4. Модифицированный метод Ньютона. 21

2.2.5. Метод секущих. 21

2.2.6. Метод итераций. 22

Глава 3. Решения систем линейных алгебраических уравнений. 26

3.1. Метод итераций. 26

3.1.1. Оценка погрешности приближений процесса итераций. 28

3.1.2. Приведение линейной системы к виду, удобному для итерации: 29

3.2. Метод Зейделя. 31

3.3. Метод релаксаций. 33

Глава 4. Решение систем нелинейных уравнений. 36

4.1. Метод Ньютона для систем нелинейных уравнений. 36

4.2. Распространение метода Ньютона на системы из n уравнений с n неизвестными 39

4.3. Метод итераций для систем нелинейных уравнений. 41

4.4. Распространение метода итераций на системы из n уравнений с n неизвестными 44

Глава 5. Интерполяция. 46

5.1. Постановка задачи интерполирования. 46

5.2. Конечные разности. 47

5.3. Интерполяционная формула Ньютона №1. 48

5.4. Интерполяционная формула Ньютона №2. 49

5.5. Интерполяционный многочлен Лагранжа. 52

5.5.1. Вычисление лагранжевых коэффициентов. 53

5.5.2. Схема Эйткина. 56

5.5.3. Остаточный член формулы Лагранжа. 58

5.6. Обратное интерполирование. 58

5.6.1 Итерационные методы для обратного интерполирования. 59

Глава 6. Аппроксимация функций с помощью сплайнов. 61

6.1. Кубические сплайны.. 62

Глава 7. Методы обработки экспериментальных данных. 65

7.1 Построение эмпирической формулы. 65

7.2. Метод выбранных точек (метод натянутой нити) 65

7.3 Метод средних. 66

7.4. Метод наименьших квадратов. 66

7.5. Метод выравнивания. 68

7.6. Метод наименьших квадратов для полиномов. 76

Глава 8. Численное интегрирование. 81

8.1. Квадратурные формулы Ньютона-Котеса. 81

8.1. Формула трапеций и ее остаточный член. 82

8.2. Общая формула трапеций и ее остаточный член. 83

8.3 Формула Симпсона и ее остаточный член. 87

8.4. Общая формула Симпсона и ее остаточный член. 87

8.5. Формулы Ньютона-Котеса высших порядков. 91

8.6. Квадратурная формула Чебышева. 91

8.7. Квадратурная формула Гаусса. 94

Глава 9. Приближенное решение обыкновенных. 101

дифференциальных уравнений. 101

9.1. Аналитические методы.. 102

9.1.1. Метод последовательного дифференцирования. 102

9.1.2. Метод последовательных приближений. 104

9.1.3 Метод неопределенных коэффициентов. 105

9.2. Численные методы.. 107

9.2.1. Метод Эйлера. 107

9.2.2. Модифицированные методы Эйлера. 109

9.2.3. Метод Рунге-Кутта для уравнений первого порядка. 111

Список литературы.. 116