Исходная задача. 2 страница

В приведенной таблице, кроме объемов потребностей и величин запасов, указаны стоимости доставки единицы товара 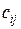со склада 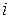потребителю ( , ).

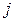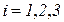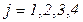Таким образом, всего в задаче имеется 12 переменных 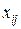. Они удовлетворяют двум группам ограничений.

Во-первых, заданы запасы на складах:

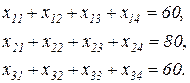(2.48)

Во-вторых, известны потребности клиентов:

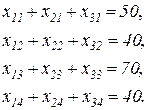(2.49)

Итак, всего имеется 7 ограничений типа равенств. Кроме того, все переменные неотрицательны – еще 12 ограничений.

Целевая функция – стоимость перевозки, которую необходимо минимизировать, имеет вид:

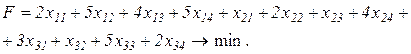(2.50)

В литературе рассматриваются различные варианты постановки и решения транспортной задачи. Количество переменных и ограничений в транспортной задаче обычно достаточно велико, и для ее решения разработаны специальные алгоритмы, реализованные в соответствующих программах. Такие программы обычно входят в популярные математические пакеты, их можно также найти в Интернете.

В нашем примере оптимальный план перевозок выглядит следующим образом.

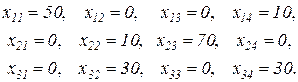
Мы видим, что все ограничения (2.48) и (2.49) выполнены, а общие затраты на перевозку товаров составили F_opt = 330 единиц.

2.4 Задачи об упаковке

В данном параграфе мы кратко рассмотрим еще один класс задач, связанных с анализом альтернатив и принятием решений. Эти задачи также относятся к задачам оптимизации, однако их особенность состоит в том, что переменные, по которым производится оптимизация, могут принимать только два значения – 0 или 1. Фактически это означает, что некоторая переменная может быть либо выбрана при решении задачи, либо нет.

2.4.1 Задача о рюкзаке

Имеется 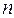предметов, которые нужно упаковать в рюкзак, суммарный вес которого не может превышать 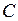. Каждый 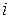-й предмет имеет стоимость 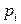и вес . Необходимо загрузить рюкзак таким образом, чтобы стоимость загруженных предметов была наибольшей, а суммарный вес рюкзака не превышал 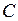. При этом предполагается, что 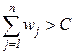, т.е. не все имеющиеся предметы поместятся в рюкзак.

К подобной постановке сводятся многие задачи: управление информационными ресурсами, загрузка корабля или самолета, размещение капитала, раскрой листов на прямоугольные заготовки и другие.

Введем 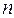-векторы и .

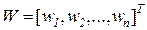Обозначим 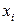переменную, определяющую выбор 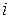-го предмета: 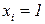, если 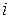-й предмет упаковывается в рюкзак, и 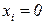в противном случае. Эти переменные образуют вектор .

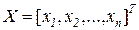Простейшая задача о рюкзаке формулируется следующим образом.

Найти

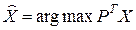(2.51)

при условиях

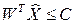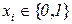, . (2.52)

Задача (2.51), (2.52) похожа на задачу линейного программирования, но особенность ограничений 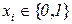не позволяет непосредственно применять, например, симплекс-метод, который может привести к нецелочисленным решениям. Однако существует большое количество методов решения этой задачи, не связанных с линейным программированием. В качестве примера приведем так называемый «жадный» алгоритм [34].

Предположим, что все предметы упорядочены по относительной стоимости:

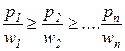. (2.53)

Тогда алгоритм может быть записан в виде следующего фрагмента программы на языке Паскаль.

begin

U:=0; Z:=0;

for j:=1 to n do

if U+w_j <= C then

begin x_j:=1; U:=U+w_j; Z:=Z+p_J end

else x_j:=0;

end.

Этот алгоритм определяет суммарный вес рюкзака U, суммарную стоимость упакованных предметов Z, а также оптимальный вектор .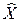

Пример. К упаковке представлено 10 предметов, параметры которых приведены в таблице 2.8. Суммарный вес предметов, как видно из таблицы, равен 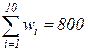кг. Общий вес рюкзака не должен превышать 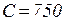кг.

В соответствии с рассмотренным алгоритмом упорядочиваем предметы по величине отношения 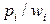, а затем начинаем наполнять рюкзак. Нетрудно видеть, что будут выбраны предметы 9,4,10,3,5,6,7,2,1, а предмет 8 в рюкзак не войдет.

Таблица 2.8

Решение задачи о рюкзаке

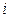
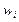
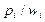
				Упорядоченные	Упорядоченные номера
				1.14
			16.7	1,85
			2,8	2,2
			1,85	2.8
			5,0	5,0
			5,83	5,45
			10,0	5,83
			5,45	10,0
			1,14	16,7
			2,2

Таким образом, вектор оптимальной загрузки имеет вид

.

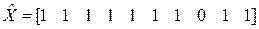Суммарный вес рюкзака получился 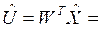745 кг.

Общая стоимость загруженных предметов

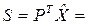1680 руб.

2.4.2 Задачи упаковки в контейнеры

Имеется множество из 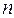предметов 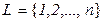, известны их веса , 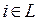. Требуется разбить множество 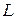на 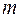подмножеств 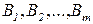, называемых контейнерами, причем величина 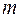заранее не известна. Каждый контейнер имеет емкость 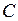, поэтому сумма весов загруженных в контейнер предметов не может превышать этой величины:

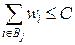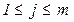, . (2.54)

К таким задачам приводит принятие решений во многих областях: погрузка штучных грузов в контейнеры, в железнодорожные вагоны, размещение файлов на магнитных дисках, формирование программы учебного курса из отдельных модулей и другие.

Задача формулируется следующим образом. Введем переменные:

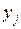={1, если j-й контейнер используется; 0 иначе},

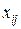={1,если i-й предмет лежит в j-м контейнере; 0 иначе}.

Требуется загрузить все предметы, используя минимальное число контейнеров:

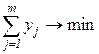, (2.55)

при этом загрузка каждого контейнера не должна превышать предельную емкость С:

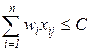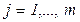, , (2.56)

а все предметы должны быть загружены:

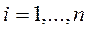, . (2.57)

Для решения задачи упаковки в контейнеры разработано множество алгоритмов [26]. Мы приведем один из них, называемый «наилучший подходящий».

Пусть предметы расположены в произвольном порядке.

· 1-й предмет помещаем в первый контейнер.

· На к-м шаге размещаем к-й предмет. Находим частично заполненные контейнеры, где для него достаточно свободного места, и выбираем среди них наиболее заполненный.

· Если таковых нет, то берем новый пустой контейнер и помещаем к-й предмет в него.

Пример. Рассмотрим упаковку предметов предыдущего примера в контейнеры, вмещающие 400 кг. Сохраняя нумерацию предметов в таблице 2.8, в соответствии с приведенным алгоритмом получаем следующую последовательность.

1-й контейнер: 5+15+43+200+10+12+10+55 = 350,

2-й контейнер: 350,

3-й контейнер: 100.

Если же предметы предварительно отсортировать по убыванию веса, то получим другую, более плотную упаковку, однако в два контейнера все предметы не войдут.

1-й контейнер: 350+43++5 = 398,

2-й контейнер: 200+100+55+15+12+10=392,

3-й контейнер: 10.

2.5 Задачи о замене оборудования

Замена оборудования – одна из важных функций управления предприятиями. Эти операции производятся либо при истечении срока службы установленного оборудования, либо при переходе предприятия на выпуск новой продукции, для которого требуется другое оборудование.

2.5.1 Простейшая задача о замене оборудования

В простейшей постановке задача о замене оборудования формулируется следующим образом [19].

Имеется некоторое оборудование, начальная стоимость которого равна 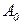. Это оборудование подвергается износу, теряя свою стоимость по закону 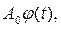где функция 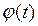определяет скорость снижения стоимости оборудования во времени. При этом принимается, что срок службы этого оборудования таков, что нет необходимости учитывать инфляционные процессы при учете стоимости оборудования и его использования.

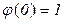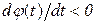
В начальный момент , 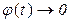при 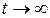, т.е. эта функция убывающая. Вид этой функции показан на рисунке 2.4 а. Степень износа оборудования оценивается формулой .

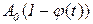Одновременно с износом возрастает стоимость обслуживания оборудования – суммарные расходы на содержание, эксплуатацию и ремонт, которые определяются функцией 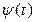. Эта функция возрастает со временем, ее вид показан на рисунке 2.4 б. Предполагается, что 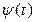не зависит от начальной стоимости оборудования. Полная себестоимость оборудования к моменту 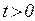становится равной .

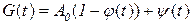В качестве показателя, который оценивает все издержки использования оборудования, обычно берут удельную себестоимость, подсчитанную за время, прошедшее с начала эксплуатации оборудования [19], т.е. показатель

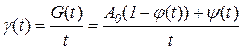. (2.58)

а б

Рис. 2.4 Вид функции снижения стоимости оборудования (а)
и повышения затрат на обслуживание (б)

Функция 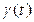при малых t убывает, а при увеличении времени проходит через минимум и начинает возрастать за счет роста расходов на обслуживание (рисунок 2.6). Таким образом, наиболее рациональный момент смены оборудования (продажи, утилизации) – это тот момент, когда функция 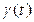достигает минимума.

2.5.2 Задача об оптимальных сроках замены дискового оборудования

Рассмотрим изложенную выше методику применительно к подсистеме дисковой памяти, предназначенной для хранения больших объемов данных в информационных системах организаций, связанных с информационными технологиями (ИТ-организаций) [14].

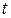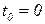
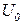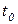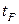Обозначим суммарный объем хранимых информационных ресурсов (ИР) в системе Мбайт, где -календарное время, месяцы. В начальный момент этот объем равен Мбайт. Рассмотрим прогноз этих величин на период от до , где 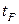- горизонт прогнозирования. Как известно, объем поступающих и хранимых в ИТ-организациях ресурсов очень быстро растет. По данным различных источников, этот рост имеет экспоненциальный характер с положительным показателем. Поэтому количество хранимых ресурсов может быть представлено в виде

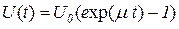, (2.59)

где 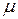- интенсивность поступления ресурсов в систему 1/мес.

Стоимость хранения и обработки ресурсов также растет, пропорционально их объему, или даже быстрей с учетом инфляции и усложнения указанных процессов. Таким образом, стоимость хранения и обработки ИР в зависимости от времени может быть представлена в виде

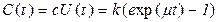. (2.60)

Здесь

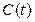- стоимость хранения и обработки всех ресурсов, руб.,

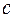- стоимость хранения и обработки единицы ресурсов, руб./Мбайт,

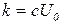- начальная стоимость ресурсов, руб.

Рассмотрим теперь динамику изменения стоимости оборудования. Как уже отмечалось, при современном уровне информационных технологий это, как правило, дисковые массивы и обслуживающее их оборудование. Стоимость оборудования снижается по мере его эксплуатации в связи с физическим и моральным износом. Зависимость, описывающую потерю стоимости оборудования, обслуживающего ресурсы, можно описать выражением

,

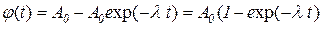где 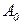- начальная стоимость оборудования, руб.,

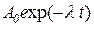- остаточная стоимость оборудования,

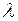- скорость снижения стоимости оборудования, 1/мес.

Таким образом, в момент 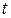полная себестоимость оборудования ресурсов становится равной

. (2.61)

Как уже отмечалось, в соответствии с теорией замены оборудования [19], наиболее адекватным показателем является среднемесячная себестоимость, вычисленная за промежуток времени от начала эксплуатации системы до текущего момента. Таким образом, мы приходим к показателю

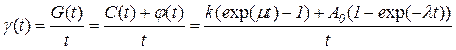, (2.62)

где 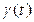- средняя себестоимость системы руб/мес. , вычисленная за период .

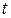Примеры графиков изменения со временем величин 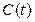, , 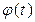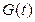и 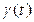приведены на рисунке 2.5. При решении вопроса о моменте замены оборудования естественно выбирать момент 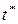, когда показатель достигнет минимума.

Момент 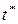можно определить численно, решив задачу однокритериальной оптимизации

,

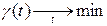а ее решение примет вид:

.

Эта задача легко решается численно, но возможно получить и ее аналитическое решение. Приравняв к нулю производную функции 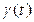, получим выражение

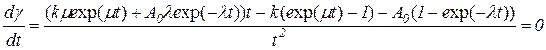. (2.63)

Это выражение обращается в нуль, когда его числитель равен нулю. После некоторых преобразований условие (2.63) можно записать в виде

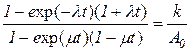. (2.64)

Соотношение (2.64) зависит от двух параметров: 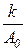и 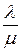, и для них можно построить номограмму, по которой определяется величина 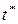. При учете инфляции вычисления усложняются, однако общая идея остается прежней.

Пример определения оптимальных сроков замены оборудования. Исследования динамики информационных ресурсов, которые проводились по данным ИТ-подразделения одного из муниципальных учреждений города Красноярска, показали, что основная нагрузка приходится на жесткие диски архивного хранения [14]. Оборудование с высокой скоростью доступа используется регулярно, но объемы информации, которые обрабатываются на этом оборудовании, не столь велики. Меньше всего задействовано оборудование со средней скоростью доступа. Кроме того, анализ динамики ресурсов за ряд лет в сочетании с экспертными оценками позволили оценить параметры модели (2.59) – (2.63) для всех классов актуальности.

В качестве примера рассчитаем оптимальные сроки смены оборудования с высокой скоростью доступа. Расчеты выполнялись для временного интервала в 5 лет: 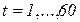c шагом 1 месяц. Качественно графики для всех видов ресурсов идентичны.

Для высокоскоростного оборудования и обработки, соответственно, ресурсов высокой актуальности приняты следующие показатели.

· начальная стоимость оборудования руб.,

· цена обслуживания руб.,

· интенсивность поступления ресурсов в систему 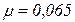1/мес.,

· скорость снижения стоимости 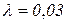1/мес.

Расчетный график величин 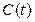, 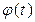и 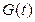приведен на рисунке 2.5, а график средней себестоимости 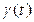показан на рисунке 2.6.

Рис.к 2.5. Графики функци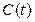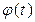й , и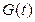

Обозначение: ‑ , ‑ , ‑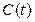

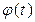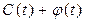Рис. 2.6. График функции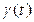

Анализируя график на рисунке 2.6, мы видим, что оптимальный срок. замены оборудования составляет 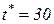мес., или 2,5 года, что по мнению экспертов, согласуется с реальной политикой ИТ-организации. В самом деле, при напряженной работе информационных систем решения о модернизации или замене дисковых массивов принимаются через 2 – 3 года.

Дальнейшее развитие данной модели связано, во-первых, с усовершенствованием методики оценки параметров в формулах (2.59) – (2.64), а во-вторых, с учетом коэффициента дисконтирования денежных средств.

2.6 Многокритериальные задачи принятия решений

В данном параграфе мы вернемся к общей постановке задачи многокритериальной оптимизации, о которой говорилось в разделе 2.3.

Напомним, что общая постановка детерминированной многокритериальной задачи параметрической оптимизации с ограничениями формулируется следующим образом [29, 34]:

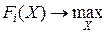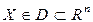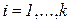, , . (2.65)

Здесь 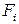, 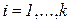– численные критерии, оценивающие качество решения, 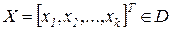– множество допустимых решений, задаваемых ограничениями:

, ,

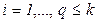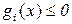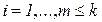, , (2.66)

где 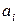, 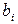- заданные числа, – заданные функции.

Задача (2,65), (2,66) не является стандартной с точки зрения традиционных методов оптимизации из-за наличия векторного критерия оптимизации. Поэтому важны различные приемы ее сведения к более удобным конструкциям, допускающим численное решение обычными средствами оптимизации. Такое сведение не является однозначным и вызывает известные трудности. Объясняется это тем, что многие из критериев являются противоречивыми: улучшение одного из них приводит к ухудшению другого. Возникает проблема выбора разумного компромисса, то есть определения такого допустимого вектора управляемых параметров 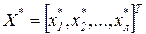, при котором все критериальные параметры принимают приемлемые значения.

Рассмотрим наиболее употребительные в практике многокритериальной оптимизации методы приведения векторного множества критериев к одному скалярному.

Метод главного критерия. В этом случае в качестве целевого критерия выбирается один из имеющегося множества критериев, который наиболее полно, по мнению ЛПР, отражает цели оптимизации. Остальные частные критерии учитываются с помощью дополнительных ограничений, которые включаются во множество 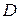. Основные трудности такого подхода связаны с назначением дополнительных ограничений. Кроме того, часто имеется несколько главных критериев, находящихся в противоречии друг с другом.

Метод линейной свертки критериев. Это наиболее простой и часто применяемый метод. Его сущность состоит в приведении задачи оптимизации к виду:

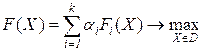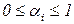, , . (2.67)

Весовые коэффициенты 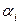назначаются ЛПР. Они могут рассматриваться как показатели относительной значимости отдельных критериев 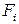. Эти показатели характеризуют чувствительность целевого критерия к изменению частных критериев: