Ниже приведены краткие сведения об онтологиях и пример их использования для моделирования процессов принятия решений в системах обучения.
Слово «онтология» имеет два значения:
· философская дисциплина, которая изучает наиболее общие характеристики бытия и сущностей;
· структура, описывающая значения элементов некоторой системы.
Неформально онтология представляет собой некоторое описание взгляда на мир применительно к конкретной области интересов. Это описание состоит из терминов и правил использования этих терминов, ограничивающих их значения в рамках конкретной области.
Структурно онтология – это система, состоящая из набора понятий и набора утверждений об этих понятиях, на основе которых можно описывать классы, отношения, функции и индивиды. Основными компонентами онтологии могут являться:
· классы (или понятия),
· отношения (или свойства, атрибуты),
· функции,
· аксиомы,
· экземпляры (или индивиды).
Классы или понятия используются в широком смысле. Понятием может быть любая сущность, о которой может быть дана какая-либо информация. Классы — это абстрактные группы, коллекции или наборы объектов. Они могут включать в себя экземпляры, другие классы, либо же сочетания и того, и другого. Классы в онтологиях обычно организованы в таксономию — иерархическую классификацию понятий по отношению включения. Например, классы Бакалавр и Магистрант являются подклассами класса Студент, который в свою очередь включен в класс Учащиеся.
Отношения представляют тип взаимодействия между понятиями предметной области. Формально n-арные отношения определяются как подмножество произведения n множеств:  . Пример бинарного отношения – отношение Часть – Целое. Отношения тоже могут быть организованы в таксономию по включению.
. Пример бинарного отношения – отношение Часть – Целое. Отношения тоже могут быть организованы в таксономию по включению.
Функции — это специальный случай отношений, в которых n-й элемент отношения однозначно определяется n-1 предшествующими элементами. Формально функции определяются следующим образом:
F: C1 Ч C2 Ч … Ч Cn-1 —> Cn.
Примерами функциональных отношений являются отношения Быть преподавателем для на множестве учащихся, или Оценка за выполненное задание, которая вычисляется в зависимости от правильности ответов на вопросы, времени выполнения и наличия подсказок.
Аксиомы используются, чтобы записать самоочевидные высказывания, которые всегда истинны. Они могут быть включены в онтологию для разных целей, например, для определения комплексных ограничений на значения атрибутов, аргументы отношений, для проверки корректности информации, описанной в онтологии, или для вывода новой информации.
В качестве примера того, что в рамках онтологий понимается под аксиомами, можно привести следующее положение и его формальную запись на языке исчисления предикатов первого порядка:
Сотрудник, являющийся заведующим кафедрой, работает на кафедре.Вводятся переменные Е (сотрудник) и P (заведующий кафедрой). Тогда аксиома записывается следующим образом:
Forall (E,P) Employee(E) and Head-Of-Chair(E,P)=> Works-At-Chair(E,P).Цели создания онтологий. В последние годы разработка онтологий – явное формальное описание терминов предметной области и отношений между ними – переходит из мира лабораторий по искусственному интеллекту на рабочие столы экспертов по предметным областям, в том числе и в области принятия решений.
Потребность в разработке онтологий возникает по ряду причин:
· анализ знаний о предметной области;
· совместное использование людьми или программными агентами общего понимания структуры информации;
· возможность повторного использования знаний в предметной области;
· представление допущений в предметной области в явном виде;
· отделение знаний в предметной области от оперативных знаний.
Методология создания онтологий. Практическая разработка онтологии включает:
· определение классов в онтологии;
· расположение классов в таксономическую иерархию (ПОДКЛАСС- НАДКЛАСС);
· определение слотов и описание их допустимых значений;
· заполнение значений слотов экземпляров.
После этого можно создать базу знаний, определив отдельные экземпляры этих классов, введя в определенный слот значение и дополнительные ограничения для слота.
Существуют некоторые фундаментальные правила разработки онтологии, которые близки к рассмотренным ранее правилам моделирования «мягких» систем.
· Не существует единственно правильного способа моделирования предметной области – всегда существуют жизнеспособные альтернативы. Лучшее решение почти всегда зависит от предполагаемого приложения и ожидаемых расширений.
· Разработка онтологии – это обязательно итеративный процесс.
· Понятия в онтологии должны быть близки к объектам (физическим или логическим) и отношениям в интересующей предметной области. Скорее всего, это существительные (объекты) или глаголы (отношения) в предложениях, которые описывают предметную область.
Знание того, для чего предполагается использовать онтологию, и того, насколько детальной или общей она будет, может повлиять на многие решения, касающиеся моделирования. Нужно определить, какая из альтернатив поможет лучше решить поставленную задачу и будет более наглядной, более расширяемой и более простой в обслуживании.
После того, как определена начальная версия онтологии, ее можно оценить и отладить, используя ее в каких-то приложениях и/или обсудив ее с экспертами предметной области. В результате начальную онтологию скорее всего нужно будет пересмотреть. И этот процесс итеративного проектирования будет продолжаться в течение всего жизненного цикла онтологии.
Для создания онтологий разработано множество языковых и программных средств. Из них отметим только так называемые редакторы онтологий. Основная функция любого редактора онтологий состоит в поддержке процесса формализации знаний и представлении онтологии как спецификации (точного и полного описания).
Одним из наиболее популярных редакторов онтологий является Protege (protege.stanford.edu), представляющий собой свободно распространяемую Java-программу, предназначенную для построения (создания, редактирования и просмотра) онтологий той или иной прикладной области. Программа включает редактор онтологий, позволяющий проектировать онтологии, разворачивая иерархическую структуру абстрактных и конкретных классов и слотов. На основе сформированной онтологии Protege позволяет генерировать формы получения знаний для введения экземпляров классов и подклассов.
Данный инструмент поддерживает использование языка OWL (Web Ontology Language, в аббревиатуре буквы намеренно переставлены местами, чтобы получилось английское слово «сова») – язык представления онтологий в Web. Он позволяет генерировать HTML-документы, отображающие структуру онтологий. В редакторе используется фреймовая модель представления знаний, что позволяет адаптировать его и для редактирования моделей предметных областей, представленных не только в OWL, но и в других форматах (UML, XML, SHOE, DAML+OIL, RDF/RDFS и т.п.).
В заключение приведем пример онтологии образовательной программы. На рисунке 2.3 приведен фрагмент онтологии, созданной с помощью редактора Protegeиописывающей структуру рабочего учебного плана подготовки бакалавров по направлению 220700.62 – Управление в технических системах.
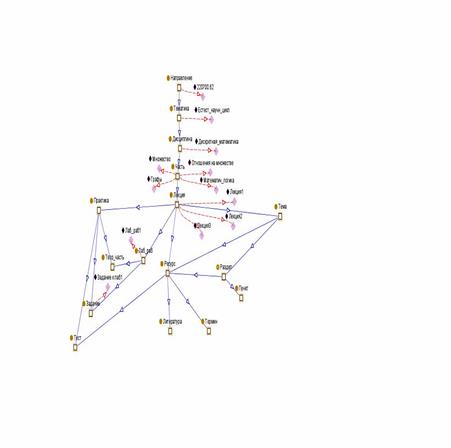
Рис. 2.3. Фрагмент онтологии учебного плана подготовки бакалавров по направлению 220700.62 «Управление в технических системах».
В этом фрагменте выделены базовые классы: направление, цикл дисциплин, дисциплина, а затем детализирован класс дисциплина, который, в свою очередь, порождает классы: раздел курса, лекция, практика и далее по мере детализации описания процесса обучения. Сплошные линии обозначают связи типа состоит из или входит в, а пунктирные – наличие других подклассов данного класса.
Полная онтология рабочего учебного плана представляет достаточно обширный документ, который, по сравнению с традиционной табличной формой, позволяет установить межпредметные связи, оценить последовательность приобретения знаний, умений и компетенций (как этого требуют образовательные стандарты 3-го поколения), а также прослеживать возможные индивидуальные траектории обучения.
2.2 Методы экспертных оценок
2.2.1 Экспертный подход к принятию решений
В широком смысле, экспертный подход предполагает создание неко-торого «мультиразума», обладающего большими способностями по сравнению с возможностями отдельного человека. Такой подход позволяет решать задачи, не поддающиеся решению обычным аналитическим способом [26].
Метод экспертных оценок является одним из реализаций экспертного подхода. Сущность этого метода заключается в проведении экспертами интуитивно-логического анализа проблемы с количественной оценкой суждений и формальной обработкой результатов. Получаемое в результате обработки обобщенное мнение экспертов принимается как решение проблемы. Комплексное использование интуиции (неосознанного мышления), логического мышления и количественных оценок с их формальной обработкой позволяет во многих случаях получить эффективное решение проблемы.
При выполнении своей роли в процессе управления эксперты производят две основные функции: формируют объекты (альтернативные ситуации, цели, решения и т.п.) и производят измерение их характеристик (вероятности свершения событий, коэффициенты значимости целей, предпочтения решений и т.п.). Формирование объектов осуществляется экспертами на основе логического мышления и интуиции. При этом большую роль играют знания и опыт экспертов. Измерение характеристик объектов требует от экспертов знания теории измерений.Существующие виды экспертных оценок можно классифицировать по следующим признакам.1. По форме участия экспертов: очное, заочное. Очный метод позволяет сосредоточить внимание экспертов на решаемой проблеме, что повышает качество результата, однако заочный метод может быть дешевле.
2. По количеству итераций (повторов процедуры для повышения точности) – одношаговые и многошаговые.
3. По решаемым задачам: генерирующие решения и оценивающие варианты.
4. По типу ответа: описательные и ранжирующие, оценивающие объект в относительной или абсолютной (численной) шкале.
5. По способу обработки мнений экспертов: непосредственные и аналитические.
6. По количеству привлекаемых экспертов: без ограничения и с ограничениями. Обычно привлекается 5 – 12 экспертов.
Эксперты должны обладать опытом в областях, соответствующих решаемым задачам. При подборе экспертов следует учитывать момент личной заинтересованности, который может стать существенным препятствием для получения объективного суждения. Наиболее распространены методы Шара, когда один эксперт, наиболее уважаемый специалист, рекомендует ряд других и далее по цепочке, пока не будет подобран необходимый коллектив.
После получения ответов экспертов необходимо провести их обработку, что позволяет получить следующие результаты.
1. Оценить согласованность мнений экспертов. При отсутствии значимой согласованности экспертов необходимо выявить причины несогласованности (наличие групп) и признать отсутствие согласованного мнения (ничтожные результаты экспертизы).
2. Оценить ошибку исследования.
3. Построить модель свойств объекта на основе ответов экспертов (для аналитической экспертизы)
4. Подготовить отчет с результатами экспертного оценивания. В отчете указывается цель исследования, состав экспертов, полученная оценка и статистический анализ результатов
Характерными особенностями метода экспертных оценок как научного инструмента решения сложных неформализуемых проблем являются, во-первых, научно обоснованная организация проведения всех этапов экспертизы, обеспечивающая наибольшую эффективность работы на каждом из этапов, и, во-вторых, применение количественных методов – как при организации экспертизы, так и при оценке суждений экспертов и формальной групповой обработке результатов. Эти две особенности отличают метод экспертных оценок от обычной давно известной экспертизы, широко применяемой в различных сферах человеческой деятельности.В настоящее время в нашей стране и за рубежом метод экспертных оценок широко применяется для решения важных проблем. В различных отраслях, объединениях и на предприятиях действуют постоянные или временные экспертные комиссии, формирующие решения по различным сложным проблемам.Все множество плохо формализуемых проблем условно можно разделить на два класса.К первому классу относятся проблемы, в отношении которых имеется достаточный информационный потенциал, позволяющий успешно решать эти проблемы. Основные трудности в решении проблем первого класса при экспертной оценке заключаются в реализации существующего информационного потенциала путем подбора экспертов, построения рациональных процедур опроса и применения адекватных методов обработки его результатов. При этом методы опроса и обработки основываются на использовании принципа «хорошего» измерителя. Данный принцип означает, что выполняются следующие гипотезы:1) эксперт является хранилищем большого объема рационально обработанной информации, и поэтому он может рассматриваться как качественный источник информации;2) групповое мнение экспертов близко к истинному решению проблемы.Если эти гипотезы верны, то для построения процедур опроса и алгоритмов обработки можно использовать результаты теории измерений и математической статистики.Ко второму классу относятся проблемы, в отношении которых информационный потенциал знаний недостаточен для уверенности в справедливости указанных гипотез. При решении проблем из этого класса экспертов уже нельзя рассматривать как «хороших измерителей». Поэтому необходимо очень осторожно проводить обработку результатов экспертизы. Применение методов осреднения, справедливых для «хороших измерителей», в данном случае может привести к большим ошибкам. Например, мнение одного эксперта, сильно отличающееся от мнений остальных экспертов, может оказаться правильным. В связи с этим для проблем второго класса в основном должна применяться качественная обработка.Область применения метода экспертных оценок весьма широка. Перечислим типовые задачи, решаемые методом экспертных оценок:1) составление перечня возможных событий в различных областях за определенный промежуток времени;2) определение наиболее вероятных интервалов времени свершения совокупности событий;3) определение целей и задач управления с упорядочением их по степени важности;4) определение альтернативных (вариантов решения задачи) с оценкой их предпочтения;5) альтернативное распределение ресурсов для решения задач с оценкой их предпочтительности;6) альтернативные варианты принятия решений в определенной ситуации с оценкой их предпочтительности.Для решения перечисленных типовых задач в настоящее время применяются различные разновидности метода экспертных оценок. К основным видам относятся: анкетирование и интервьюирование; мозговой штурм, метод Дельфи, дискуссия, совещание, оперативная игра, сценарий.Каждый из этих видов экспертного оценивания обладает своими преимуществами и недостатками, определяющими рациональную область применения. Во многих случаях наибольший эффект дает комплексное применение нескольких видов экспертизы.Анкетирование и сценарий предполагают индивидуальную работу эксперта. Интервьюирование может осуществляться как индивидуально, так и с группой экспертов. Остальные виды экспертизы предполагают коллективное участие экспертов, в работе. Независимо от индивидуального или группового участия экспертов в работе целесообразно получать информацию от множества экспертов. Это позволяет получить на основе обработки данных более достоверные результаты, а также новую информацию о зависимости явлений, событий, фактов, суждений экспертов, не содержащуюся в явном виде в высказываниях экспертов.В настоящем курсе нет возможности подробно рассмотреть все множество видов экспертного оценивания и методов обработки их результатов. Мы остановимся только на одном из простейших методов – методе средних баллов, который может реализовываться в двух видах – методе средних арифметических рангов и методе медиан рангов.
2.2.2 Методы средних баллов
Рассмотрим простейший способ экспертного оценивания альтернатив – балльные оценки. Членов сформированной группы экспертов просят выставить баллы объектам, изделиям, технологическим процессам, предприятиям, проектам, заявкам на выполнение научно-исследовательских работ, идеям, проблемам, программам, политикам и т.п., а затем рассчитывают средние баллы и рассматривают их как интегральные оценки, выставленные коллективом опрошенных, как результаты работы «мультиразума».
При этом возникает вопрос: какими формулами пользоваться для вычисления средних величин? Ведь видов средних величин очень много. По традиции обычно применяют среднее арифметическое. Однако специалисты утверждают, что такой способ некорректен, поскольку баллы обычно измерены в так называемой порядковой шкале. В качестве средних баллов обоснованным является использование медиан. В то же время полностью игнорировать средние арифметические нерационально из-за их привычности и распространенности. Поэтому целесообразно использовать одновременно оба метода – и метод средних арифметических рангов (баллов), и методов медианных рангов. Такая рекомендация находится в согласии с концепцией устойчивости, рекомендующей использовать различные методы для обработки одних и тех же данных с целью выделить выводы, получаемые одновременно при всех методах.
Пример сравнения восьми проектов.Рассмотрим конкретный пример применения сформулированного выше подхода [26]. По заданию руководства фирмы анализировались восемь проектов, предлагаемых для включения в план стратегического развития фирмы. Они были зашифрованы следующим образом: П1,П2,П3,П4,П5,П6,П7,П8. Все проекты были направлены 12 экспертам, назначенным правлением фирмы. В таблице 2.2 приведены ранги восьми проектов, присвоенные им каждым из 12 экспертов в соответствии с их представлением о целесообразности включения проекта в стратегический план фирмы. При этом ранг 1 – самый лучший проект, который обязательно надо реализовать, ранг 2 – второй по привлекательности проект, и т.д., ранг 8 – наиболее сомнительный проект.
Анализируя результаты работы экспертов (т.е. упомянутую таблицу 2.2), члены правления фирмы были вынуждены констатировать, что полного согласия между экспертами нет, а потому данные таблицы следует подвергнуть более тщательному математическому анализу.
Метод средних арифметических рангов.Сначала был применен метод средних арифметических рангов. Для этого, прежде всего, была подсчитана сумма рангов, присвоенных проектам. Затем эта сумма была разделена на число экспертов, в результате рассчитан средний арифметический ранг (именно эта операция дала название методу). По средним рангам строится итоговая ранжировка, исходя из принципа – чем меньше средний ранг, тем лучше проект. Наименьший средний ранг, равный 2,625, у проекта П4, следовательно, в итоговой ранжировке он получает ранг 1. Следующая по величине сумма, равная 3,125, у проекта П3, – и он получает итоговый ранг 2. Проекты П2 и П6 имеют одинаковые суммы (равные 3,25), значит, с точки зрения экспертов они равноценны (при рассматриваемом способе сведения вместе мнений экспертов), а потому они должны бы стоять на 3 и 4 местах и получают средний балл (3+4)/2 = 3,5. Дальнейшие результаты приведены в таблице 2.2.
Таблица 2.2
Ранги 8 проектов по степени привлекательности
для включения в план стратегического развития фирмы
| № эксперта | П1 | П2 | П3 | П4 | П5 | П6 | П7 | П8 |
| 2,5 | 2,5 | |||||||
Примечание к таблице 2.2 . Эксперт № 4 считает, что проекты П3 и П4 равноценны, но уступают лишь одному проекту - проекту П6. Поэтому проекты П3 и П4 должны были бы стоять на втором и третьем местах и получить баллы 2 и 3. Поскольку они равноценны, то получают средний балл (2+3)/2 = 5/2 = 2,5.
Итак, ранжировка по суммам рангов (или, что то же, по средним арифметическим рангам) имеет вид:
П4  П3
П3  {П2,П6}
{П2,П6}  П1
П1 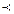 П7
П7 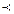 П5
П5 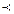 П8. (2.2)
П8. (2.2)
Здесь запись типа "А 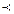 Б" означает, что проект А предшествует проекту Б (т.е. проект А лучше проекта Б). Поскольку проекты П2 и П6 получили одинаковую сумму баллов, то по рассматриваемому методу они эквивалентны, а потому объединены в группу (в фигурных скобках). Таким образом, итог расчетов – ранжировка (2.2), и на ее основе предстоит принимать решение.
Б" означает, что проект А предшествует проекту Б (т.е. проект А лучше проекта Б). Поскольку проекты П2 и П6 получили одинаковую сумму баллов, то по рассматриваемому методу они эквивалентны, а потому объединены в группу (в фигурных скобках). Таким образом, итог расчетов – ранжировка (2.2), и на ее основе предстоит принимать решение.
Метод медиан рангов.Но тут необходимо напомнить, что ответы экспертов измерены в порядковой шкале, а потому для них не вполне правомерно проводить усреднение методом средних арифметических. Более подходящим является использование метода медиан.
Это означает, что надо взять ответы экспертов, соответствующие одному из проектов, например, проекту П1. Это ранги 5, 5, 1, 6, 8, 5, 6, 5, 6, 5, 7, 1. Затем их надо расположить в порядке неубывания. Получим последовательность: 1, 1, 5, 5, 5, 5, 5, 6, 6, 6, 7, 8. На центральных местах – шестом и седьмом – стоят цифры 5 и 5. Следовательно, медиана равна 5.
Таблица 2.3
Результаты расчетов по методу средних арифметических
и методу медиан для данных, приведенных в табл.2.2
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | П8 | |
| Сумма рангов | 37,5 | 31.5 | ||||||
| Среднее арифметическое рангов | 3,25 | 3,125 | 2,625 | 6,333 | 3,25 | 5,333 | 7,083 | |
| Итоговый ранг по среднему арифметическому | 3,5 | 3,5 | ||||||
| Медианы рангов | 2,25 | 7,5 | ||||||
| Итоговый ранг по медианам | 2,5 | 2,5 |
Медианы совокупностей из 12 рангов, соответствующих определенным проектам, приведены в предпоследней строке таблицы. (При этом медианы вычислены по обычным правилам статистики - как среднее арифметическое центральных членов вариационного ряда). Итоговое упорядочение по методу медиан приведено в последней строке таблицы. Ранжировка (т.е. упорядочение – итоговое мнение комиссии экспертов) по медианам имеет вид:
П4 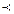 {П2, П3}
{П2, П3} 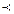 П6
П6 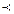 П1
П1 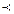 П7
П7 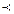 П8
П8 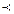 П5. (2.3)
П5. (2.3)
Поскольку проекты П2 и П3 имеют одинаковые медианы баллов, то по рассматриваемому методу ранжирования они эквивалентны, а потому объединены в группу (кластер).
Сравнение ранжировок по методу средних арифметических и методу медиан.Сравнение ранжировок (2.2) и (2.3) показывает их близость. Можно принять, что проекты П3, П2, П6 упорядочены как П3 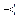 П2
П2 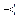 П6, но из-за погрешностей экспертных оценок в одном методе признаны равноценными проекты П2 и П6 (ранжировка (2.2)), а в другом - проекты П3 и П2 (ранжировка (2.3)). Существенным является только расхождение, касающееся упорядочения проектов П8 и П5: в ранжировке (2.2) П5
П6, но из-за погрешностей экспертных оценок в одном методе признаны равноценными проекты П2 и П6 (ранжировка (2.2)), а в другом - проекты П3 и П2 (ранжировка (2.3)). Существенным является только расхождение, касающееся упорядочения проектов П8 и П5: в ранжировке (2.2) П5 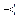 П8, а в ранжировке (2.3), наоборот, П8
П8, а в ранжировке (2.3), наоборот, П8 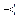 П5. Однако эти проекты - наименее привлекательные из восьми рассматриваемых, и при выборе наиболее привлекательных проектов для дальнейшего обсуждения и использования на это расхождение можно не обращать внимания.
П5. Однако эти проекты - наименее привлекательные из восьми рассматриваемых, и при выборе наиболее привлекательных проектов для дальнейшего обсуждения и использования на это расхождение можно не обращать внимания.
Рассмотренный пример демонстрирует сходство и различие ранжировок, полученных по методу средних арифметических рангов и по методу медиан, а также пользу от их совместного применения.
Мы рассмотрели простейший пример экспертного оценивания вариантов решения. На практике используются более сложные и совершенные методы, их поддержка осуществляется с помощью информационных систем поддержки принятия решений СППР.
2.3 Методы оптимизации в задачах принятия решений
Как отмечалось ранее, принятие решений часто связано с учетом множества противоречивых требований, удовлетворить которым одновременно в полной мере невозможно. Математически такая ситуация приводит к задачам, которые получили название задач многокритериальной оптимизации.
Общая постановка детерминированной многокритериальной задачи параметрической оптимизации с ограничениями формулируется следующим образом [34]:
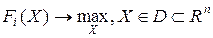 ,
, 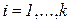 . (2.4)
. (2.4)
В этой формуле 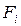 ,
, 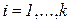 представляют собой численные критерии, оценивающие качество решения. Множество
представляют собой численные критерии, оценивающие качество решения. Множество 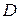 называется множеством допустимых решений. В пределах этого множества может задаваться ряд ограничений на вектор
называется множеством допустимых решений. В пределах этого множества может задаваться ряд ограничений на вектор  :
:
· прямые (интервальные) ограничения
 ,
, 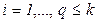 ; (2.5а)
; (2.5а)
· функциональные ограничения
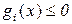 ,
, 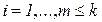 , (2.5б)
, (2.5б)
где 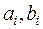 - заданные числа,
- заданные числа,  – заданные функции.
– заданные функции.
Предполагается, что каждый из критериальных параметров 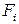 необходимо максимизировать. Это не ограничивает общности, так как минимизация функции
необходимо максимизировать. Это не ограничивает общности, так как минимизация функции  эквивалентна максимизации
эквивалентна максимизации 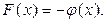 Аналогично, замена знака у левой части неравенства
Аналогично, замена знака у левой части неравенства 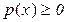 меняет знаки неравенств на противоположные и приводит их к виду
меняет знаки неравенств на противоположные и приводит их к виду 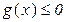 .
.
В том случае, когда критерий всего один 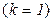 , получается классическая задача однокритериальной оптимизации. Такие задачи мы и рассмотрим в первую очередь.
, получается классическая задача однокритериальной оптимизации. Такие задачи мы и рассмотрим в первую очередь.
Ниже, в основном, пойдет речь о постановках задач оптимизации. Что касается численных алгоритмов решения таких задач, то мы, за исключением некоторых простых случаев, их не приводим, полагая, во-первых, что численные методы изучены ранее в курсах прикладной математики, а во-вторых, что эти методы доступны в математических пакетах и сети Интернет.
2.3.1 Принятие решений на основе методов линейного программирования
Среди оптимизационных задач в теории принятия решений наиболее известны задачи линейного программирования, в которых максимизируемая функция 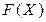 в выражении (2.4) является линейной, а ограничения
в выражении (2.4) является линейной, а ограничения  задаются линейными неравенствами [34,37].
задаются линейными неравенствами [34,37].
Базовая формулировка задачи линейного программирования выглядит следующим образом.
Дата добавления: 2015-09-07; просмотров: 1493;
