Исходная задача. 3 страница
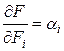 ,
, 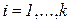 .
.
Сложность данного метода заключается в необходимости экспертного задания весовых коэффициентов 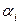 , особенно тогда, когда частные критерии различны по характеру, размерности и величине. В этом случае их предварительно следует привести к безразмерному виду, нормированному к единице. Пусть
, особенно тогда, когда частные критерии различны по характеру, размерности и величине. В этом случае их предварительно следует привести к безразмерному виду, нормированному к единице. Пусть 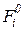 – максимальное значение критерия
– максимальное значение критерия  ,
, 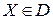 . Тогда безразмерный нормированный критерий
. Тогда безразмерный нормированный критерий 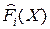 примет вид:
примет вид:
 ,
, 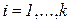 .
.
Иногда вместо аддитивного критерия (2.67) используется критерий с мультипликативной сверткой частных критериев:
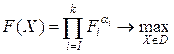 . (2.68)
. (2.68)
Этот критерий принципиально не отличается от предыдущего, так как можно прологарифмировать выражение (2.68) (предполагается, что все  ) и получить выражение, аналогичное (2.67):
) и получить выражение, аналогичное (2.67):
 .
.
Метод минимаксных критериев. Этот метод в простейшем случае применяется в следующем виде:
 . (2.69)
. (2.69)
В отличие от метода линейной свертки, здесь на целевой критерий оказывает влияние только тот частный критерий оптимизации, которому соответствует наименьшее значение функции  . Таким образом, в данном случае решение принимается с учетом наиболее «слабого» критерия. При необходимости можно, как и в предыдущем случае, ввести весовые коэффициенты
. Таким образом, в данном случае решение принимается с учетом наиболее «слабого» критерия. При необходимости можно, как и в предыдущем случае, ввести весовые коэффициенты 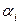 . Тогда критерий (2.69) примет вид
. Тогда критерий (2.69) примет вид
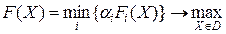 ,
, 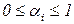 ,
,  .
.
Другой подход к созданию минимаксных критериев заключается в выборе контрольных показателей по всем критериям 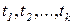 , которые определяют их наименьшее допустимое значение
, которые определяют их наименьшее допустимое значение 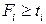 . При этом в качестве скалярного критерия можно использовать величину наибольшего отклонения значения критерия от контрольного показателя, которую необходимо минимизировать:
. При этом в качестве скалярного критерия можно использовать величину наибольшего отклонения значения критерия от контрольного показателя, которую необходимо минимизировать:
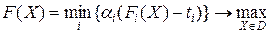 ,
, 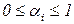 ,
,  .
.
Контрольные показатели определяются либо экспертно, либо путем решения однокритериальных задач:
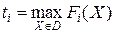 .
.
В последнем случае набор чисел  характеризует предельные, вообще говоря, недостижимые значения критериев.
характеризует предельные, вообще говоря, недостижимые значения критериев.
На практике подбор чисел  может осуществляться ЛПР в интерактивном режиме при работе с программой, вычисляющей значения критериев
может осуществляться ЛПР в интерактивном режиме при работе с программой, вычисляющей значения критериев  .
.
Метод Парето. Метод Парето позволяет находить компромиссы между требованиями к принимаемому решению, которые определяются частными критериями.
Рассмотрим 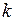 - мерное пространство
- мерное пространство 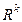 , образованное критериями
, образованное критериями  ,
, 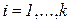 . В этом пространстве каждому вектору
. В этом пространстве каждому вектору  соответствует вектор
соответствует вектор
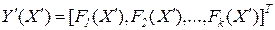 .
.
Рассмотрев все векторы 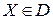 , получим область
, получим область 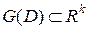 , которая представляет собой отображение множества допустимых решений
, которая представляет собой отображение множества допустимых решений 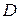 в пространство
в пространство 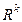 , или область достижимости рассматриваемой многокритериальной задачи. Обозначим границу области достижимости
, или область достижимости рассматриваемой многокритериальной задачи. Обозначим границу области достижимости 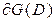
Рассмотрим две точки 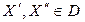 . Если выполняются неравенства
. Если выполняются неравенства
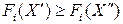 (2.70)
(2.70)
для всех 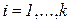 , причем хотя бы одно неравенство строгое, то будем говорить, что точка
, причем хотя бы одно неравенство строгое, то будем говорить, что точка 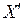 предпочтительнее точки
предпочтительнее точки 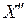 . Если для некоторой точки
. Если для некоторой точки 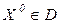 не существует более предпочтительных точек, то точку
не существует более предпочтительных точек, то точку 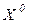 называют эффективным, или Парето-оптимальным решением многокритериальной задачи (2.65).
называют эффективным, или Парето-оптимальным решением многокритериальной задачи (2.65).
Множество, включающее все эффективные решения, обозначается 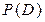 и называется множеством Парето для векторного отображения
и называется множеством Парето для векторного отображения 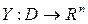 . Образ множества
. Образ множества 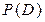 в пространстве критериев
в пространстве критериев 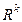 обозначается
обозначается 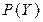 . Это множество содержится в области достижимости рассматриваемой задачи, т.е.
. Это множество содержится в области достижимости рассматриваемой задачи, т.е. 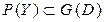 .
.
Пример. Проиллюстрируем введенные понятия простым примером.
Рассмотрим задачу оптимизации с двумя критериями:
 (2.71)
(2.71)
при ограничениях
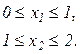 (2.72)
(2.72)
На рисунке 2.7 а показана область ограничений переменных D –прямоугольник 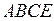 , а на рисунке 2.7 б – область достижимости задачи
, а на рисунке 2.7 б – область достижимости задачи  в пространстве критериев в виде четырехугольника
в пространстве критериев в виде четырехугольника  .
.

а б
Рис. 2.7. Область ограничений переменных 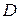 (а) и область достижимости задачи
(а) и область достижимости задачи  (б) в задаче (2.71), (2.72)
(б) в задаче (2.71), (2.72)
Можно непосредственными вычислениями убедиться, что все эффективные точки лежат на прямой 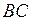 , принадлежащей области
, принадлежащей области 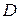 . Таким образом, множество Парето
. Таким образом, множество Парето 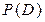 представляет собой линию
представляет собой линию 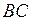 , а отображение этой линии в пространство критериев
, а отображение этой линии в пространство критериев 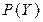 - линию
- линию 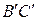 .
.
Итак, мы видим, что решение данной двухкритериальной задачи оптимизации представляет собой множество 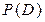 . Для выбора из этого компромиссного множества единственного решения необходимо привлечение дополнительной информации в виде одного из рассмотренных выше методов. Рассмотрим применение этих методов к данной задаче.
. Для выбора из этого компромиссного множества единственного решения необходимо привлечение дополнительной информации в виде одного из рассмотренных выше методов. Рассмотрим применение этих методов к данной задаче.
Метод главного критерия. Предположим, что главным критерием оптимизации является  , а критерий
, а критерий  ограничен условием
ограничен условием
 .
.
Тогда мы получаем обычную однокритериальную задачу линейного программирования:
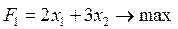
при условиях
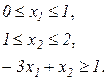 (2.73)
(2.73)
Решение данной задачи имеет вид: 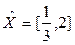 , ему на рисунке 2.7 а соответствует точка
, ему на рисунке 2.7 а соответствует точка 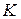 , при этом вектор критериев равен
, при этом вектор критериев равен 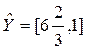 , ему на рисунке 2.7 б соответствует точка
, ему на рисунке 2.7 б соответствует точка 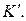 Мы видим, что
Мы видим, что 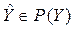 , то есть полученное решение принадлежит множеству Парето.
, то есть полученное решение принадлежит множеству Парето.
Метод линейной свертки критериев. Введем весовые коэффициенты 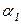 для критерия
для критерия  и
и 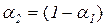 для критерия
для критерия  . Сведем задачу (2.71), (2.72) к однокритериальной:
. Сведем задачу (2.71), (2.72) к однокритериальной:
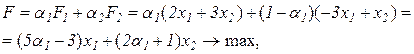 (2.74)
(2.74)
при ограничениях (2.59).
Из формулы (2.74) видно, что при 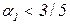 коэффициент при
коэффициент при  отрицательный, следовательно, для максимизации критерия (2.61) необходимо выбрать наименьшую возможную величину
отрицательный, следовательно, для максимизации критерия (2.61) необходимо выбрать наименьшую возможную величину 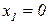 , а при
, а при  этот коэффициент положительный, и необходимо выбрать наибольшую возможную величину
этот коэффициент положительный, и необходимо выбрать наибольшую возможную величину 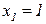 . Переменная
. Переменная  в обоих случаях должна быть равной 2.
в обоих случаях должна быть равной 2.
В первом случае имеем:
 ,
,  ,
, 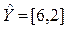 .
.
Обратившись к рисункам 2.7а и 2.7 б, мы видим, что при 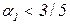 решение данной задачи соответствует точкам
решение данной задачи соответствует точкам 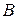 и
и  .
.
При 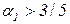 получается следующее решение
получается следующее решение
 ,
, 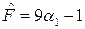 ,
, 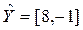
что соответствует точкам 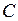 и
и 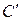 на рисунках.
на рисунках.
Отметим, что в обоих случаях решение находится в области Парето.
Использование минимаксного критерия.Обратимся к формуле (2.69). В рассматриваемом случае она имеет вид:
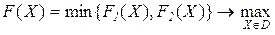 .
.
Анализ области достижимости  показывает, что в пределах этой области выполняется условие
показывает, что в пределах этой области выполняется условие 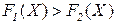 , то есть минимальное значение имеет критерий
, то есть минимальное значение имеет критерий 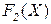 , и его в соответствии с (2.69) необходимо максимизировать. Нетрудно видеть, что
, и его в соответствии с (2.69) необходимо максимизировать. Нетрудно видеть, что 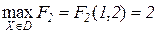 , что соответствует точке
, что соответствует точке 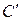 на рисунке 2.7 б, которая принадлежит множеству Парето.
на рисунке 2.7 б, которая принадлежит множеству Парето.
Подводя итоги второй главы, мы видим, что существует множество методов, основанных на детерминированном подходе к формированию альтернатив решения и выбору среди них наилучшего.
Однако, как отмечалось ранее, детерминированный подход не учитывает возможных неопределенностей в условиях принятия решений, их случайного характера. Поэтому в следующей главе будут рассмотрены методы, основанные на вероятностном подходе к принятию решения.
Вопросы и задания для самостоятельного изучения
1. Составьте когнитивную карту какой-либо знакомой Вам деятельности, например, успехов в спорте, в учебе, в научной работе и др.
2. Выберите знакомую Вам область и проранжируйте входящие в нее объекты (например, марки автомобилей, футбольные команды, изучаемые Вами дисциплины и др.). Сравните ранжировки, полученные по методу средних арифметических и по методу медиан.
3. Предположим, Вы отправляетесь в поход и собираете рюкзак. Предельный вес рюкзака для юношей – 10 кг, для девушек – 5 кг. Составьте список возможных вещей и продуктов, их веса и цены, а затем решите задачу об упаковке рюкзака с помощью описанного выше алгоритма.
4. Вернемся к предыдущей задаче. Предположим, выбранные Вами вещи нужно нести в сумках весом не более 2 кг. Определите количество необходимых сумок и загрузку каждой из них.
5. Составьте на свой вкус суточное меню из 4–5 продуктов, исходя из следующих условий: суточная потребность в белках – 80 г, жиров – 100 г, углеводов – 360 г. Общая калорийность меню для юношей 2700 ккал, для девушек – 2300 ккал. Сформулируйте и решите задачу линейного программирования для определения количества продуктов в двух вариантах:
а) минимальная стоимость при балансе по белкам, жирам и углеводам и общей калорийности.
б). минимальный вес продуктов при таком же балансе.
в). сформулируйте двухкритериальную задачу на основе задач а) и б). и решите ее методом линейной свертки критериев, задавшись весом каждого из критериев по формуле (2.67).
Калорийность продуктов найдите в Интернете, а их стоимость – в ближайшем магазине. Для решения задачи используйте программу симплекс‑метода, которую тоже можно найти в Интернете.
6. Определите оптимальный срок смены автомобиля по методике п. 2.5.1 при следующих условиях (время рассчитывается в месяцах):
а) начальная цена автомобиля 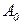 рублей,
рублей,
б) потеря стоимости определяется формулой 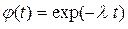 ,
,
в) стоимость обслуживания возрастает по закону 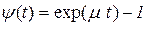 .
.
Решите задачу при 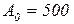 тыс. рублей,
тыс. рублей,  ,
, 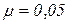 .
.
Проанализируйте влияние параметров 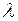 и
и 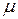 на оптимальный срок замены автомобиля. Как изменится срок замены, если функция
на оптимальный срок замены автомобиля. Как изменится срок замены, если функция 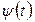 будет зависеть от
будет зависеть от 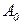 ?
?
Глава 3 Вероятностные модели формирования и выбора альтернатив решений
В настоящей главе мы рассмотрим вероятностные модели поддержки процессов принятия решений. Из всего множества методов, разработанных в этой области, мы остановимся на двух: теории цепей Маркова и теории формирования оптимального инвестиционного портфеля Г. Марковица.
3.1 Моделирование систем на основе формализма цепей Маркова
Наиболее простой класс динамических вероятностных моделей дискретно-стохастического типа (P – схемы по классификации, рассмотренной в первой главе) образуют цепи Маркова, названные так по имени известного русского математика А.А. Маркова, разработавшего эту теорию в 1907 году. Большой вклад в теорию цепей Маркова внес академик А.Н. Колмогоров [8, 15, 17, 27].
Этот математический аппарат оказывается удобным, в частности, при описании функционирования и анализа работы вычислительных систем [6]. Однако возможности теории цепей Маркова далеко выходят за рамки описания процессов оценки и принятия решений. Эта теория широко применяется в физике, биологии, социологии, экономике, технике и целом ряде других наук.
Математический аппарат цепей Маркова позволяет оценивать многие характеристики информационных процессов, такие как вероятное время завершения определенных этапов работы, средняя производительность, среднее время безотказной работы и другие, что необходимо при принятии проектных решений. Здесь приводятся только начальные сведения об этих моделях. Более подробно теория и применение цепей Маркова рассматривается в специальной литературе [6,15,17]. Ряд задач, приводящих к марковским цепям, рассматривается в разделах 3.2 - 3.4.
3.1.1 Определение и динамика цепи Маркова [11]
Рассмотрим систему å, находящуюся в каждый из дискретных моментов 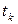 в одном из
в одном из 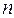 состояний
состояний 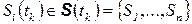 .
.
Система рассматривается в моменты времени, образующие множество 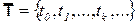 . В каждый момент времени система может находиться только в одном из состояний. Состояния изменяются со временем случайным образом. Это изменение определяется матрицей переходных вероятностей
. В каждый момент времени система может находиться только в одном из состояний. Состояния изменяются со временем случайным образом. Это изменение определяется матрицей переходных вероятностей
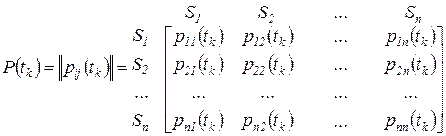 . (3.1)
. (3.1)
Каждый элемент матрицы  определяет вероятность того, что если å в момент
определяет вероятность того, что если å в момент 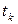 находилось в состоянии
находилось в состоянии 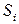 , то в момент
, то в момент 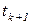 она окажется в состоянии
она окажется в состоянии  :
:
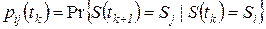 . (3.2)
. (3.2)
Причем (и это основное свойство марковских процессов) вероятность перехода из 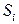 в
в  не зависит от предыдущих состояний.
не зависит от предыдущих состояний.
Понятно, что переходы во все возможные состояния (в том числе в себя) образуют полную группу событий, поэтому 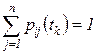 для всех
для всех 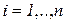 ,
, 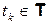 .
.
Пусть вектор-строка 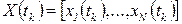 - описывает распределение вероятностей нахождения å в соответствующих состояниях в момент
- описывает распределение вероятностей нахождения å в соответствующих состояниях в момент 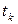 , то есть
, то есть 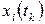 - это вероятность того, что в момент
- это вероятность того, что в момент 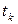 å находится в состоянии
å находится в состоянии 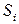 . При этом
. При этом 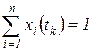 ,
, 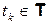 . Тогда по теореме об умножении вероятностей и с учетом основного свойства марковского процесса получим:
. Тогда по теореме об умножении вероятностей и с учетом основного свойства марковского процесса получим:
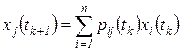 , (3.3)
, (3.3)
где  выступают в роли условных вероятностей перехода в состояние
выступают в роли условных вероятностей перехода в состояние  при условии, что система находится в состоянии
при условии, что система находится в состоянии 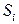 .
.
Нетрудно видеть, что правая часть написанной формулы определяет произведение вектора  на матрицу
на матрицу  и в векторной форме эквивалентна следующей записи динамического процесса:
и в векторной форме эквивалентна следующей записи динамического процесса:
 . (3.4)
. (3.4)
Последовательность состояний 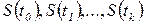 называется конечной цепью Маркова. Цепь называется однородной, если
называется конечной цепью Маркова. Цепь называется однородной, если  не зависит от времени.
не зависит от времени.
В этом случае рекуррентная формула (3.4) может быть записана в виде
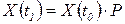 ,
,
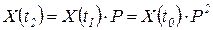 ,
,
…·
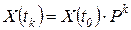 , (3.5)
, (3.5)
где 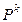 - k-я степень матрицы P.
- k-я степень матрицы P.
Нетрудно убедиться, что сумма вероятностей нахождения системы во всех состояниях (т.е. сумма элементов вектора  ) на каждом шаге остается равной единице.
) на каждом шаге остается равной единице.
Последовательность векторов 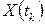 ,
, 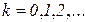 определяет динамику моделируемого процесса.
определяет динамику моделируемого процесса.
Отметим, что матрицы P, порождающие цепи Маркова, т.е. такие, у которых все элементы 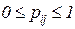 , а их суммы по столбцам равны единице для всех строк:
, а их суммы по столбцам равны единице для всех строк: 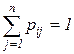 ,
, 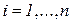 , называют стохастическими.
, называют стохастическими.
Рассмотрим классификацию состояний цепи Маркова. Множество всех состояний может быть разбито на непересекающиеся подмножества, или классы: невозвратные и эргодические. Их свойства определяются следующим образом. Если процесс покинул класс состояний первого типа, он никогда в него не возвращается. Если процесс попал в класс состояний второго типа, то он никогда его не покидает. Невозвратное множество мы будем обозначать 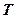 , а эргодическое -
, а эргодическое -  . При этом
. При этом 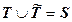 ,
, 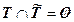 . Если эргодическое множество содержит только одно состояние, то это состояние называется поглощающим. Для такого состояния
. Если эргодическое множество содержит только одно состояние, то это состояние называется поглощающим. Для такого состояния 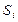 элемент переходной матрицы
элемент переходной матрицы  должен быть равен 1, следовательно, все остальные элементы соответствующей строки равны 0. Цепь, все эргодические состояния которой являются поглощающими, называется поглощающей цепью.
должен быть равен 1, следовательно, все остальные элементы соответствующей строки равны 0. Цепь, все эргодические состояния которой являются поглощающими, называется поглощающей цепью.
Для цепи Маркова с 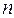 состояниями, в которой имеются как невозвратные, так и эргодические множества, структура матрицы вероятностей переходов (возможно, после перенумерации состояний) имеет канонический вид
состояниями, в которой имеются как невозвратные, так и эргодические множества, структура матрицы вероятностей переходов (возможно, после перенумерации состояний) имеет канонический вид

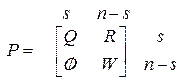 (3.6)
(3.6)
где 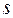 - количество состояний в невозвратном множестве;
- количество состояний в невозвратном множестве;
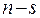 - количество состояний в эргодическом множестве.
- количество состояний в эргодическом множестве.
Матрица Q размерности  определяет поведение процесса до выхода из множества невозвратных состояний.
определяет поведение процесса до выхода из множества невозвратных состояний.
Матрица R размерности  определяет вероятности перехода из множества невозвратных состояний в эргодическое множество.
определяет вероятности перехода из множества невозвратных состояний в эргодическое множество.
Матрица 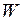 размерности
размерности 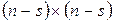 определяет динамику эргодических состояний.
определяет динамику эргодических состояний.
Поскольку из множества  невозможно выйти, то матрица
невозможно выйти, то матрица  размерности
размерности 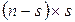 состоит из нулей.
состоит из нулей.
При возведении матрицы P в степень перемножаются блоки, указанные в (3.9), и произвольная степень канонической матрицы имеет вид
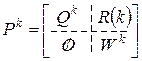 . (3.7)
. (3.7)
3.1.2 Оценка длительности пребывания процесса
во множестве невозвратных состояний
Рассмотрим поведение цепи Маркова при росте числа шагов k. Из анализа структуры матрицы  (3.7) следует, что процесс, стартовав из некоторого состояния
(3.7) следует, что процесс, стартовав из некоторого состояния 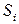 , принадлежащего невозвратному множеству
, принадлежащего невозвратному множеству 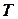 , на каждом шаге с вероятностями, определенными матрицей
, на каждом шаге с вероятностями, определенными матрицей 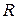 , переходит в эргодическое множество
, переходит в эргодическое множество  . Через определенное число шагов процесс окажется в
. Через определенное число шагов процесс окажется в  с вероятностью, как угодно близкой к единице.
с вероятностью, как угодно близкой к единице.
При моделировании реальных систем с помощью конечных цепей Маркова часто бывает необходимо оценивать показатели продолжительности работы системы или трудоемкости процессов. Для этой цели нужно уметь рассчитывать число шагов, в течение которых процесс не покидает множество 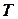 («время жизни» процесса), а также «время жизни» отдельных состояний этого множества.
(«время жизни» процесса), а также «время жизни» отдельных состояний этого множества.
Дата добавления: 2015-09-07; просмотров: 2079;
