Исходная задача. 4 страница
Обозначим 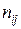 общее число моментов времени (тактов работы системы), проведенных процессом в состоянии
общее число моментов времени (тактов работы системы), проведенных процессом в состоянии  при условии, что он стартовал из состояния
при условии, что он стартовал из состояния 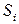 (
( 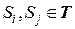 ). Понятно, что
). Понятно, что 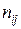 - случайная величина, принимающая целочисленные значения
- случайная величина, принимающая целочисленные значения 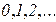 с соответствующими вероятностями, которые мы будем обозначать
с соответствующими вероятностями, которые мы будем обозначать 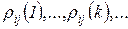 . Таким образом,
. Таким образом,  - вероятность того, что система за все «время жизни» процесса находилась в состоянии
- вероятность того, что система за все «время жизни» процесса находилась в состоянии  , при старте из
, при старте из 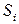 ,
, 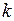 раз. При этом
раз. При этом 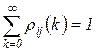 . Зная распределение вероятностей
. Зная распределение вероятностей 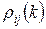 , можно вычислить все необходимые статистические характеристики процесса – математическое ожидание, дисперсию и другие. Однако вычисление таких распределений в общем случае – достаточно сложная задача, поэтому мы ограничимся в данном разделе рассмотрением двух более простых практически важных задач:
, можно вычислить все необходимые статистические характеристики процесса – математическое ожидание, дисперсию и другие. Однако вычисление таких распределений в общем случае – достаточно сложная задача, поэтому мы ограничимся в данном разделе рассмотрением двух более простых практически важных задач:
- вычисление математического ожидания величин 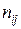 , т.е.
, т.е. 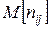 и средних значений трудоемкости процесса;
и средних значений трудоемкости процесса;
- вычисление дисперсий 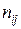 , т.е.
, т.е.  и среднеквадратичных отклонений трудоемкости процесса.
и среднеквадратичных отклонений трудоемкости процесса.
Переходя к вычислению матожидания величины 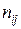 , начнем с изучения свойств матрицы
, начнем с изучения свойств матрицы 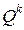 , входящей в структуру
, входящей в структуру 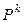 в формуле (3.7). Поскольку по определению все элементы матрицы Q
в формуле (3.7). Поскольку по определению все элементы матрицы Q 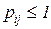 и
и  (в отличие от матрицы
(в отличие от матрицы  , для которой
, для которой 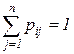
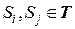 ), то при больших
), то при больших 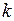 эта матрица стремится к нулевой, т.е.
эта матрица стремится к нулевой, т.е. 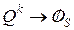 при
при 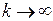 . Здесь
. Здесь 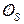 - нулевая квадратная матрица s-го порядка.
- нулевая квадратная матрица s-го порядка.
Для дальнейшего нам понадобится формула, оценивающая матрицу матожиданий числа пребываний процесса во множестве невозвратных состояний N. Рассмотрим тождество
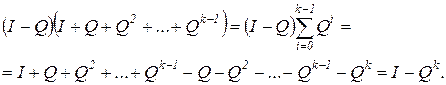
Поскольку при 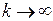
 , то
, то 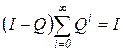 .
.
Матрица 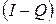 неособенная, т.к.
неособенная, т.к. 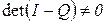 , в чем легко убедиться.
, в чем легко убедиться.
Следовательно, существует обратная матрица 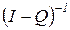 , которая играет большую роль при изучении марковских процессов с матрицей переходных вероятностей вида (3.6). Эту матрицу называют фундаментальной и обозначают
, которая играет большую роль при изучении марковских процессов с матрицей переходных вероятностей вида (3.6). Эту матрицу называют фундаментальной и обозначают
 . (3.8)
. (3.8)
Перейдем теперь к оценке среднего «время жизни» состояний процесса, относящихся к невозвратному множеству.
Обозначим, как и прежде, через 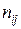 общее число моментов времени, проводимых процессом в состоянии
общее число моментов времени, проводимых процессом в состоянии  при условии, что он начался из состояния
при условии, что он начался из состояния 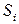 . Эта функция определена только для невозвратного множества, т.е.
. Эта функция определена только для невозвратного множества, т.е. 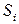 ,
, 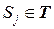 .
.
Можно показать, что матрица математических ожиданий чисел 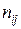 равна N, т.е.
равна N, т.е. 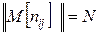 , где
, где 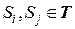 . (3.9)
. (3.9)
Для того, чтобы в этом убедиться, введем вспомогательную переменную (индикатор)  , которая принимает единичное значение, если процесс, стартовав при
, которая принимает единичное значение, если процесс, стартовав при 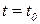 из
из 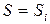 , оказывается при
, оказывается при 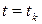 в
в 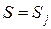 , т.е.
, т.е.
|
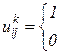
Вероятность того, что 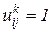 , обозначим
, обозначим  .
.
Легко видеть, что  .
.
Оценим теперь матожидание матрицы, образованной элементами 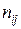 . По формуле матожидания случайной величины с дискретным распределением имеем:
. По формуле матожидания случайной величины с дискретным распределением имеем:
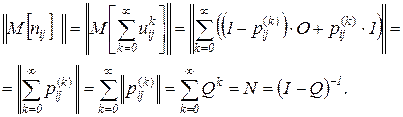
Здесь  - элемент
- элемент 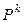 ,
,  .
.
Таким образом, среднее число шагов, которое проводит процесс в невозвратном состоянии,  , начавшись в
, начавшись в 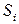 , всегда конечно и определяется i-й строкой матрицы
, всегда конечно и определяется i-й строкой матрицы 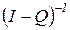 .
.
Отсюда следует, что матрица математических ожиданий числа пребываний системы в невозвратных состояниях равна фундаментальной матрице цепи Маркова:
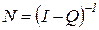 , (3.10)
, (3.10)
где I – единичная матрица.
Каждый элемент 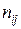 матрицы
матрицы 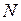 представляет собой среднее число пребываний процесса в состоянии Sj при старте из состояния
представляет собой среднее число пребываний процесса в состоянии Sj при старте из состояния 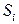 .В том случае, когда старт происходит из состояния
.В том случае, когда старт происходит из состояния 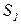 , достаточно рассматривать только первую строку матрицы
, достаточно рассматривать только первую строку матрицы 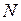 .
.
Зная  , можно вычислить среднюю трудоемкость процесса по формуле
, можно вычислить среднюю трудоемкость процесса по формуле
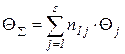 , (3.11)
, (3.11)
где - 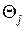 трудоемкость j – го шага процесса в соответствующих единицах.
трудоемкость j – го шага процесса в соответствующих единицах.
В ряде случаев исследователя может интересовать оценка дисперсии трудоемкости процесса. Для этой цели вычисляется матрица дисперсий числа пребываний процесса в множестве невозвратных состояний по формуле, которую мы приводим без вывода:
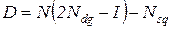 , (3.12)
, (3.12)
где индексы 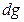 и
и 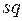 обозначают соответственно выделение диагональных элементов матрицы
обозначают соответственно выделение диагональных элементов матрицы 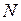 и возведение в квадрат каждого элемента этой матрицы.
и возведение в квадрат каждого элемента этой матрицы.
3.1.3 Оценка поведения цепей Маркова при большом числе шагов
В этом параграфе рассмотрен класс задач, связанных с оценкой предельных вероятностей пребывания системы в состояниях эргодического множества.
Как было выяснено выше, динамика смены состояний однородной цепи Маркова определяется поведением матрицы 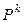 при
при 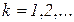 . Однако непосредственное применение формулы (3.2) для определения переходных характеристик этого процесса, в частности, скорости сходимости к предельным вероятностям пребывания в различных состояниях при
. Однако непосредственное применение формулы (3.2) для определения переходных характеристик этого процесса, в частности, скорости сходимости к предельным вероятностям пребывания в различных состояниях при 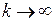 , не всегда удобно.
, не всегда удобно.
Для оценки скорости сходимости можно привести матрицу  к диагональному виду с помощью линейного преобразования. Предположим, что матрица
к диагональному виду с помощью линейного преобразования. Предположим, что матрица  имеет
имеет 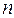 различных собственных чисел
различных собственных чисел 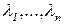 . Тогда ее можно привести к виду
. Тогда ее можно привести к виду
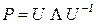 , (3.13)
, (3.13)
где 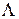 - диагональная матрица
- диагональная матрица
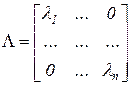 ,
,
а матрица 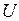 составлена из собственных векторов матрицы
составлена из собственных векторов матрицы  так, что i-й столбец матрицы
так, что i-й столбец матрицы 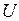 является собственным вектором матрицы
является собственным вектором матрицы 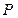 при собственном числе
при собственном числе  .
.
Напомним, что i-е собственное число матрицы 
 , есть i-й корень алгебраического уравнения
, есть i-й корень алгебраического уравнения
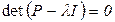 , (3.14)
, (3.14)
а собственный вектор 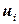 , соответствующий собственному числу
, соответствующий собственному числу  есть решение линейного уравнения
есть решение линейного уравнения
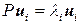 . (3.15)
. (3.15)
Преобразование (3.13) удобно тем, что при возведении в степень матрицы  фактически возводится в степень только диагональная матрица
фактически возводится в степень только диагональная матрица 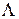 :
:
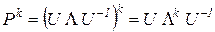 , (3.16)
, (3.16)
причем
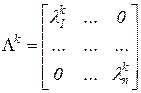 . (3.17)
. (3.17)
Таким образом, динамику изменения матрицы 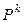 легко оценить по поведению
легко оценить по поведению 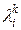 ,
,  .
.
Мы уже упоминали, что матрица  , определяющая однородную цепь Маркова, является стохастической матрицей [8]. Особенностью этой матрицы является то, что ее максимальное собственное число
, определяющая однородную цепь Маркова, является стохастической матрицей [8]. Особенностью этой матрицы является то, что ее максимальное собственное число 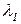 равно 1, и ему соответствует собственный вектор, составленный из единиц:
равно 1, и ему соответствует собственный вектор, составленный из единиц: 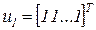 .
.
Возможен еще один способ нахождения предельных вероятностей. Исходя из того, что 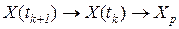 при
при 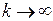 , уравнение (3.4) можно записать в виде
, уравнение (3.4) можно записать в виде 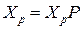 , добавив условие
, добавив условие 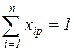 , а затем решить полученную систему уравнений.
, а затем решить полученную систему уравнений.
Пример. В качестве примера исследования поведения цепи Маркова при большом числе шагов рассмотрим систему с двумя состояниями 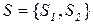 , описываемую матрицей
, описываемую матрицей
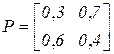 ,
,
с начальным распределением вероятностей  .
.
Требуется найти предельное распределение вероятностей нахождения в состояниях 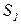 ,
,  при большом числе шагов
при большом числе шагов 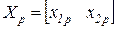 .
.
Задачу решим тремя разными способами.
1. Путем численного возведения матрицы  в высокую степень. Из формулы (3.5) следует, что
в высокую степень. Из формулы (3.5) следует, что 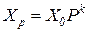 ,
, 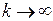 , однако на практике достаточно взять достаточно большое
, однако на практике достаточно взять достаточно большое 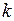 , например,
, например, 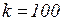 . Проделав вычисления, получим
. Проделав вычисления, получим
 .
.
2. Путем спектрального разложения матрицы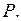
Найдем собственные числа матрицы  по формуле (3.14):
по формуле (3.14):
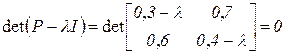 ,
,
откуда 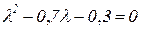 ,
,  ,
, 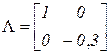 .
.
Определим собственные векторы 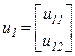 ,
, 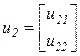 .
.
По формуле (3.15) для 
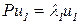 ,
, 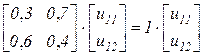 .
.
Полученное уравнение недоопределено, поэтому, приняв 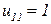 , получим
, получим 
 .
.
Аналогично для  имеем уравнение
имеем уравнение
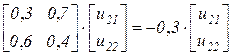 и, приняв
и, приняв 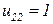 , получим
, получим 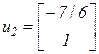 .
.
Следовательно, матрица 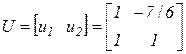 ,
,
а обратная к ней матрица  .
.
Таким образом, спектральное представление матрицы P имеет вид
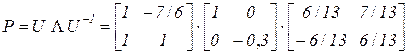 .
.
Теперь можно вычислить предельное распределение вероятностей:
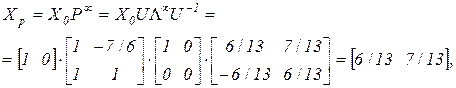
что совпадает с результатами предыдущих вычислений.
3. Исходя из того, что 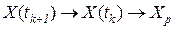 при
при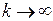 , уравнение (3.4) можно записать в виде
, уравнение (3.4) можно записать в виде 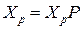 , добавив условие
, добавив условие 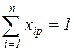 .
.
Получаем систему уравнений:

Решая эту систему с двумя неизвестными, в которой одно из уравнений (первое или второе) лишнее, получим уже знакомый ответ  .
.
В следующих параграфах рассмотрены два содержательных примера описания процессов принятия решений в рамках формализма цепей Маркова.
3.2 Модель процесса обучения как цепь Маркова
На рисунке 3.1 представлена цепь Маркова, моделирующая процесс прохождения обучаемым фрагмента некоторого учебного курса и содержащая десять узлов, соответствующих различным шагам процесса обучения.
В модели на рисунке 3.1 выделены следующие состояния: S1 – изучение первого раздела (модуля) теоретического материала; S2, S3 – ответы на вопросы по первому разделу; S4 – изучение материала второго раздела (по этому разделу не предусмотрен контроль); S5 - изучение теоретического материала третьего раздела; S6 – S9 - ответы на вопросы по третьему разделу; S10 – завершение изучения третьего раздела. Из рисунка видно, что состояния S1 – S9 относятся к множеству невозвратных состояний, S10 - поглощающее состояние.
Заданы оценки трудоемкостей прохождения каждого узла:
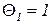 час,
час, 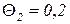 часа,
часа, 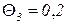 часа,
часа, 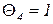 час,
час,
 часа,
часа, 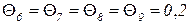 часа.
часа.

Рис. 3.1. Цепь Маркова, моделирующая процесс прохождения фрагмента учебного курса
Матрица вероятностей переходов 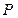 имеет вид:
имеет вид:
 . (3.18)
. (3.18)
Начальное распределение вероятностей  означает, что процесс обучения всегда стартует из первого состояния.
означает, что процесс обучения всегда стартует из первого состояния.
Средние значения числа пребываний процесса в множестве невозвратных состояний, вычисленные по формуле (3.10), задаются следующей матрицей:
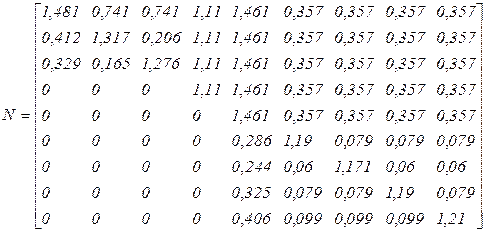 .
.
Средняя трудоемкость процесса:

Вычислив матрицу дисперсий D по формуле (3.12) и взяв значения элементов первой строки, соответствующей стартовому состоянию процесса, получим среднеквадратичное отклонение трудоемкости процесса от средней
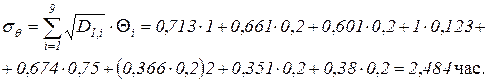

Рис. 3.2. Вероятности пребывания процесса в различных состояниях
На рисунке 3.2 приведен график распределения вероятностей прохождения отдельных этапов курса, рассчитанный по формуле (3.2) . Из него, в частности видны вероятности завершения процесса за заданное число шагов (переход в состояние S10). Из рисунка 3.3 видно, что минимальное число шагов, необходимое для завершения фрагмента курса, равно 5. Вероятность такого исхода, согласно рисунку, равна 0,337, а достаточно надежное завершение курса наступает на 9 – 13 шагах.
3.3 Система обслуживания заявок с очередью и отказами
В данном разделе мы рассмотрим модель системы, обслуживающей поступающие извне заявки. Анализ и принятие решений о параметрах таких систем представляют собой актуальные задачи системного анализа, которые возникают во многих прикладных областях, например, при обслуживании потока задач в вычислительных системах, управлении взлетом и посадкой самолетов, обработке поступающего сырья на производстве и других.
Пусть имеется обслуживающее устройство на вход которого поступают заявки, выстраивающиеся в очередь, которая вмещает 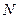 заявок (рисунок 3.3). Число одновременно поступивших заявок не превышает
заявок (рисунок 3.3). Число одновременно поступивших заявок не превышает 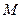 .
.

Рис. 3.3. Схема обслуживающего устройства с очередью
Система работает в дискретном времени следующим образом. В начале каждого такта устройство извлекает из очереди и начинает обслуживать только одну заявку (если очередь не пуста), а затем поступают новые заявки. Количество поступающих на вход очереди заявок 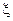 представляет собой случайную величину со следующим распределением:
представляет собой случайную величину со следующим распределением:
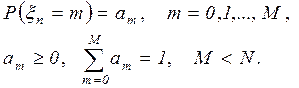
Величины 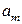 считаются заданными и представляют вероятность того, что на вход очереди поступит
считаются заданными и представляют вероятность того, что на вход очереди поступит 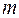 заявок. Состояние системы
заявок. Состояние системы 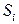 определяется как число заявок
определяется как число заявок 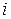 , ждущих обслуживания к началу
, ждущих обслуживания к началу 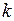 -го такта. Всего число возможных состояний системы равно
-го такта. Всего число возможных состояний системы равно 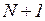 , учитывая, что очередь может быть пуста. При этом, если
, учитывая, что очередь может быть пуста. При этом, если 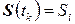 , то
, то 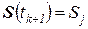 , причем номер состояния
, причем номер состояния 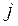 на следующем такте определяется выражением:
на следующем такте определяется выражением:
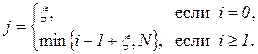
Обратим внимание на то, что число заявок в системе не может превысить  , и «лишние» заявки получают отказ.
, и «лишние» заявки получают отказ.
Составим модель системы в виде цепи Маркова. Для наглядности ограничимся следующими параметрами:  ,
,  ; распределение вероятностей поступления заявок:
; распределение вероятностей поступления заявок: 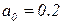 ,
, 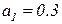 ,
, 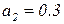 ,
,  . Будем также считать, что в начальный момент времени очередь пуста. Граф соответствующей цепи Маркова показан на рисунке 3.4.
. Будем также считать, что в начальный момент времени очередь пуста. Граф соответствующей цепи Маркова показан на рисунке 3.4.

Рис. 3.4. Модель системы обслуживания заявок с очередью и
отказами в виде цепи Маркова.
Составим матрицу переходных вероятностей для данной модели:
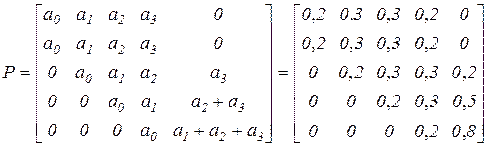 .
.
Динамику системы определяет вектор вероятностей нахождения в различных состояниях 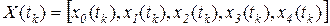 ,
, 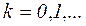 , который в начальный момент имеет вид
, который в начальный момент имеет вид 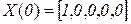 .
.
определим предельные вероятности пребывания системы в каждом из состояний при заданных выше вероятностях. Для этого, в соответствии с разделом 3.1.3, вычислим с помощью системы Mathcad высокую степень матрицы P:
 ,
,
а затем вектор предельного распределения вероятностей
 .
.
Теперь можно определить среднюю длину очереди в рассмотренной системе. По правилам вычисления математического ожидания для дискретного распределения имеем:
 .
.
Таким образом, мы выяснили, что в данной системе средняя длина очереди составляет около 3,5 заявок. Зная среднее время выполнения одной заявки  , можно определить среднее время выполнения поступившей в систему заявки:
, можно определить среднее время выполнения поступившей в систему заявки:  . В данном выражении учитывается как время ожидание в очереди, так и время непосредственного выполнения заявки.
. В данном выражении учитывается как время ожидание в очереди, так и время непосредственного выполнения заявки.
3.4 Модель динамики информационных ресурсов
Современным специалистам по информационным технологиям приходится иметь дело с хранением и обработкой больших объемов разнообразных информационных ресурсов (ИР) и принимать решения по управлению ими в процессе проектирования и эксплуатации информационных систем.
Информационные ресурсы различаются своим назначением и форматами. Принятая в настоящее время классификация ИР основана на так называемой модели Дублинского ядра метаданных [14, 41].
Всего в рамках этой системы выделено девять типов ресурсов. Ниже приводится перечень типов с пояснениями, принятыми разработчиками.
· Коллекция. Множество, содержащее элементы. Ресурс описывается как группа, части ресурса могут быть описаны отдельно, к ним осуществлен отдельный доступ.
· Данные. Информация представлена в определенной структуре (например, списки, таблицы, базы данных), обеспечивающей возможность прямой машинной обработки.
· Событие. Непродолжительное, ограниченное во времени явление. Метаданные для события могут определять цель, место, длительность, субъектов события и связи с другими событиями и ресурсами. Примером являются выставки, конференции, семинары, презентации, представления, дискуссия и др.
Дата добавления: 2015-09-07; просмотров: 2087;

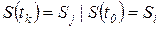 ,
в противном случае.
,
в противном случае.