Исходная задача. 5 страница
· Изображение. Ресурс, первично предназначенный служить для визуального представления, отличного от текста. К данному типу относятся изображения и фотографии физических объектов, рисунки, чертежи, мультипликация, фильмы, диаграммы, карты, музыкальная нотация.
· Интерактивный объект. Объект данного типа требует взаимодействия с пользователем для того, чтобы быть понятым, исполненным или реализованным. Примеры: интерактивные формы на веб-страницах, апплеты, обучающие средства, чаты, виртуальная реальность.
· Сервис. Система, которая выполняет одну или более функцию для конечного пользователя. Примеры: службы фотокопирования, банковский сервис, служба аутентификации, межбиблиотечный абонемент, веб-сервер.
· Программные средства. Компьютерная программа в исходном или компилированном коде, которая пригодна в неизменном виде для инсталляции на другой машине.
· Аудио. Ресурс, первоначально предназначенный служить для звукового представления. Например, аудио компакт-диск, запись речи или звуков.
· Текст. Ресурс, первоначально представляющий собой слова для чтения (книги, письма, газеты, стихи, статьи, диссертации, рукописи и др.).
Ценность информации, содержащейся в конкретном информационном ресурсе, может быть различной, кроме того, она изменяется во времени. Как все на свете, информационный ресурс рождается, живет и умирает. Поэтому можно говорить о жизненном цикле информационного ресурса.
Если исходить из классификации бизнес-процессов, рассмотренных в работе [45], информационный ресурс в период своего существования проходит следующие этапы жизненного цикла:
· сбор информации, создание ИР,
· хранение,
· обработка (упорядочение, поиск, изменение и обновление),
· архивирование,
· уничтожение.
В течение жизненного цикла меняется актуальность информации, содержащейся в информационном ресурсе. С этой точки зрения информация может классифицироваться как критическая, важная и маловажная [14].
Как правило, актуальность информации уменьшается с течением времени, следовательно, указанные классы актуальности наступают последовательно.
Исходя из сказанного, модель жизненного цикла информационного ресурса (ИР) может быть упрощенно представлена в виде цепи Маркова, графическая схема которой показана на рисунке 3.5.

Рис. 3.5. Модель жизненного цикла информационного ресурса
Здесь выделено 8 состояний, смысл которых приведен ниже;
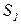 - создание ИР,
- создание ИР,
 - хранение ИР критической важности,
- хранение ИР критической важности,
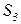 - обработка ИР критической важности,
- обработка ИР критической важности,
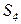 - хранение ИР с важной информацией,
- хранение ИР с важной информацией,
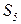 - обработка ИР с важной информацией,
- обработка ИР с важной информацией,
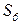 - архивирование и хранение ИР с маловажной информацией,
- архивирование и хранение ИР с маловажной информацией,
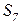 - обработка ИР с маловажной информацией,
- обработка ИР с маловажной информацией,
 - удаление ИР.
- удаление ИР.
Переход из одного состояние 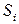 в другое
в другое  за один временной шаг является случайным событием, вероятность которого
за один временной шаг является случайным событием, вероятность которого 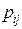 определяется этапами жизненного цикла ИР, их «временем жизни» и другими факторами. В целом, модель определится следующей матрицей переходных вероятностей размерности 8
определяется этапами жизненного цикла ИР, их «временем жизни» и другими факторами. В целом, модель определится следующей матрицей переходных вероятностей размерности 8 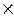 8.
8.
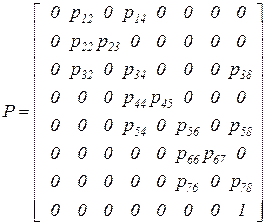 . (3.19)
. (3.19)
Вероятности перехода, как мы видели в предыдущих разделах, определяют также среднюю продолжительность пребывания информационного ресурса в каждом из выделенных состояний.
Рассмотрим методику оценки динамики информационного ресурса, основанную на приведенной выше модели жизненного цикла информационного ресурса. Для снижения размерности задачи объединим этапы хранения и обработки в один этап: 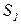 и
и  ,
, 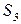 и
и  ,
, 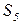 и
и 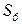 . Упрощенная модель жизненного цикла в виде цепи Маркова с дискретным временем, содержащей пять состояний, показана на рисунке 3.6.
. Упрощенная модель жизненного цикла в виде цепи Маркова с дискретным временем, содержащей пять состояний, показана на рисунке 3.6.
Здесь:
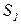 - создание ИР,
- создание ИР,
 - хранение и обработка ИР критической важности,
- хранение и обработка ИР критической важности,
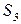 - хранение и обработка ИР с важной информацией,
- хранение и обработка ИР с важной информацией,
 - архивирование и хранение ИР с маловажной информацией,
- архивирование и хранение ИР с маловажной информацией,
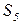 - удаление ИР.
- удаление ИР.
Пусть имеется множество информационных ресурсов R = { 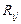 }, где по приведенной выше классификации
}, где по приведенной выше классификации 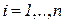 ‑ вид ИР,
‑ вид ИР, 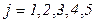 ‑ степень актуальности ресурса. Каждый ресурс поступает в информационную систему и проходит в ней весь жизненный цикл.
‑ степень актуальности ресурса. Каждый ресурс поступает в информационную систему и проходит в ней весь жизненный цикл.

Рис. 3.6. Упрощенная модель жизненного цикла информационного ресурса
Вероятности перехода между состояниями ресурса 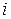 ‑го вида задаются матрицей
‑го вида задаются матрицей
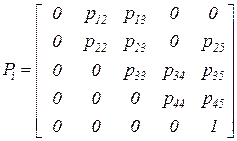 . (3.20)
. (3.20)
Ресурс 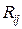 характеризуется следующими параметрами:
характеризуется следующими параметрами:
· время поступления ИР в информационную систему 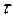 (например, дни, месяцы),
(например, дни, месяцы), 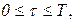 где
где  - время исследования системы;
- время исследования системы;
· объем поступившего ресурса 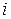 - го вида в момент
- го вида в момент 
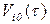 , Мбайт;
, Мбайт;
· 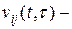 объем ресурса
объем ресурса 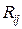 , Мбайт, в момент
, Мбайт, в момент 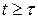 . Величины
. Величины 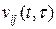 образуют вектор
образуют вектор 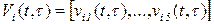 , при этом
, при этом 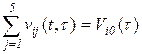 ,
, 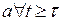 ;
;
· 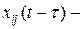 вероятность нахождения ресурса
вероятность нахождения ресурса 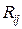 в
в 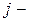 степени актуальности в момент
степени актуальности в момент 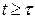 . Вероятности
. Вероятности  образуют вектор
образуют вектор 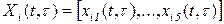 , при этом
, при этом 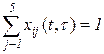 , начальное распределение вероятностей
, начальное распределение вероятностей 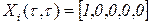 .
.
Ресурс, поступивший на вход системы (в состояние 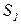 ), в дальнейшем перераспределяется между состояниями пропорционально вероятностям пребывания системы в данном состоянии. Исходя из сказанного, мы получим следующие расчетные формулы.
), в дальнейшем перераспределяется между состояниями пропорционально вероятностям пребывания системы в данном состоянии. Исходя из сказанного, мы получим следующие расчетные формулы.
Динамика изменения состояния ИР определится уравнениями:
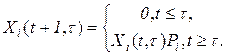 (3.21)
(3.21)
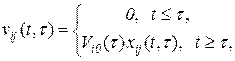 (3.22)
(3.22)
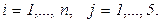
Общий объем ресурсов 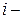 го вида, находящихся в системе, определится вектором
го вида, находящихся в системе, определится вектором
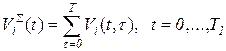 , (3.23)
, (3.23)
где 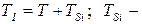 время жизни ресурса
время жизни ресурса 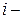 го вида.
го вида.
Общий объем ресурсов 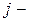 й степени актуальности определится суммой
й степени актуальности определится суммой
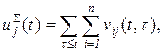 (3.24)
(3.24)
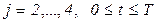 .
.
Расчетный объем ИР 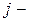 ой степени актуальности
ой степени актуальности  для определения необходимых параметров запоминающего устройства равен максимальному значению величины
для определения необходимых параметров запоминающего устройства равен максимальному значению величины 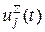 на всем исследуемом интервале времени:
на всем исследуемом интервале времени:
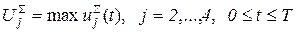 . (3.25)
. (3.25)
Расчеты по формулам (3.21) – (3.25) для матрицы (3.20) и исходных данных по объемам поступающих ресурсов удобно производить с помощью специальной программы [14].
Пример.Рассмотрим систему, содержащую информационный ресурс, динамика которого задается матрицей 
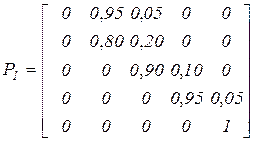 .
.
Предположим, что на вход системы в каждый момент времени поступает ресурс в объеме 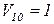 Мбайт. Расчет, проведенный по формулам (3.21) – (3.24), позволяет оценить динамику накопления ИР в системе. Результаты расчета приведены на рисунке 3.7.
Мбайт. Расчет, проведенный по формулам (3.21) – (3.24), позволяет оценить динамику накопления ИР в системе. Результаты расчета приведены на рисунке 3.7.

а

б
Рис. 3.5. Графики жизненного цикла информационного ресурса
за 100 шагов, динамика которого задана матрицей  :
:
а) – вероятности нахождения единичного ИР в разных степенях актуальности; б) – динамика накопления ИР
3.5 Принятие решений об оптимизации инвестиционного портфеля
В данном параграфе мы рассмотрим классическую задачу об оптимизации инвестиционного портфеля. Рассмотренная ниже модель носит название теории оптимизации инвестиционного портфеля Гарри Марковица, который предложил ее в 1952 году [43]. Эта теория получила широкое распространение и развитие и впоследствии была удостоена Нобелевской премии по экономике.Г. Марковиц предположил, что величины доходности ценных бумаг (облигаций) являются случайными величинами, распределенными по нормальному (гауссовскому) закону. Поэтому инвестор, формируя свой портфель, оценивает только два показателя – ожидаемую доходность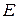 и стандартное отклонение
и стандартное отклонение 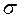 как меру риска (только эти два показателя определяют плотность распределения случайной величины при нормальном законе). Кроме того, он исходил из предположения о том, что инвестирование рассматривается как одноразовый процесс, т.е. полученный в результате инвестирования доход не реинвестируется.Рассмотрим математическую модель процесса оптимизации инвестиционного портфеля в простейшей постановке.На рынке имеется некоторое количество ценных бумаг
как меру риска (только эти два показателя определяют плотность распределения случайной величины при нормальном законе). Кроме того, он исходил из предположения о том, что инвестирование рассматривается как одноразовый процесс, т.е. полученный в результате инвестирования доход не реинвестируется.Рассмотрим математическую модель процесса оптимизации инвестиционного портфеля в простейшей постановке.На рынке имеется некоторое количество ценных бумаг 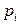 ,
, 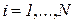 , каждая их которых характеризуется средним уровнем доходности
, каждая их которых характеризуется средним уровнем доходности 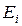 , лежащим в пределах от
, лежащим в пределах от  до
до 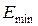 , или в относительных единицах от +1 до –1. Каждая ценная бумага
, или в относительных единицах от +1 до –1. Каждая ценная бумага 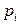 характеризуется также определенным уровнем риска, который является случайной величиной, подчиняющейся нормальному закону распределения с математическим ожиданием
характеризуется также определенным уровнем риска, который является случайной величиной, подчиняющейся нормальному закону распределения с математическим ожиданием 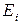 и стандартным отклонением от среднего
и стандартным отклонением от среднего 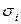 . Кроме того, риски по бумагам могут быть статистически связаны, т.е. между ними может существовать зависимость, определяемая коэффициентами корреляции
. Кроме того, риски по бумагам могут быть статистически связаны, т.е. между ними может существовать зависимость, определяемая коэффициентами корреляции  , которые могут находиться в диапазоне
, которые могут находиться в диапазоне 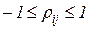 ,
, 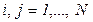 .Требуется составить инвестиционный портфель
.Требуется составить инвестиционный портфель 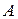 , включающий эти ценные бумаги, в котором доля бумаги
, включающий эти ценные бумаги, в котором доля бумаги 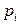 составляет
составляет 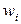 ,
, 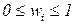 причем
причем 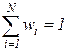 . (3.26)При этом ожидаемая суммарная доходность портфеля составит
. (3.26)При этом ожидаемая суммарная доходность портфеля составит 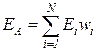 , (3.27)а суммарный риск портфеля определится выражением для дисперсии
, (3.27)а суммарный риск портфеля определится выражением для дисперсии 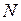 статистически связанных случайных величин:
статистически связанных случайных величин: 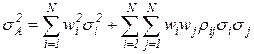 . (3.28)Предположим, что нам известны все величины
. (3.28)Предположим, что нам известны все величины 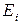 ,
, 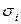 ,
,  ,
, 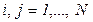 . Инвестор при принятии решения может рассматривать следующие альтернативы.1. При выбранных весах
. Инвестор при принятии решения может рассматривать следующие альтернативы.1. При выбранных весах 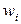 (
( 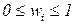 ,
, 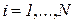 ) оценить суммарную доходность
) оценить суммарную доходность  и степень риска
и степень риска 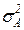 .2. Определить веса ценных бумаг
.2. Определить веса ценных бумаг 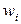 ,
, 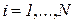 , которые обеспечат наименьший суммарный риск, т.е. минимум функции
, которые обеспечат наименьший суммарный риск, т.е. минимум функции 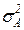 , и вычислить соответствующую доходность.3. Определить оптимальный по стоимости портфель
, и вычислить соответствующую доходность.3. Определить оптимальный по стоимости портфель 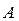 при заданном уровне риска
при заданном уровне риска 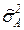 .Рассмотрим решение этих задач.В первом случае задача сводится к простым вычислениям по формулам (3.27) и (3.28).Во втором случае мы имеем задачу оптимизации:
.Рассмотрим решение этих задач.В первом случае задача сводится к простым вычислениям по формулам (3.27) и (3.28).Во втором случае мы имеем задачу оптимизации:  (3.29)при условиях:
(3.29)при условиях: 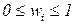 ,
, 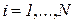 ,
, 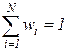 . (3.30)В третьем случае также необходимо решить задачу оптимизации
. (3.30)В третьем случае также необходимо решить задачу оптимизации 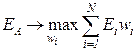 (3.31)при условиях
(3.31)при условиях 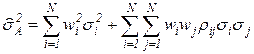 , (3.32)
, (3.32) 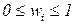 ,
, 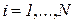 ,
, 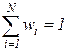 .Портфель, полученный при решении второй и третьей задачи, называют эффективным портфелем. Для решения сформулированных и более сложных задач оптимизации инвестиционного портфеля разработаны специальные алгоритмы и программы. Мы рассмотрим особенности задачи выбора портфеля на простом частном случае, когда портфель содержит всего две бумаги, т.е. когда
.Портфель, полученный при решении второй и третьей задачи, называют эффективным портфелем. Для решения сформулированных и более сложных задач оптимизации инвестиционного портфеля разработаны специальные алгоритмы и программы. Мы рассмотрим особенности задачи выбора портфеля на простом частном случае, когда портфель содержит всего две бумаги, т.е. когда  . В этом случае формулы (3.26), (3.27) и (3.28) примут соответственно следующий вид:
. В этом случае формулы (3.26), (3.27) и (3.28) примут соответственно следующий вид: 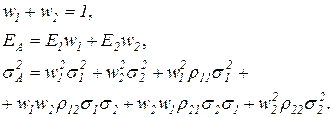 (3.33)Учитывая, что
(3.33)Учитывая, что 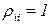 и
и  ,
,  , а также приведя подобные члены в последнем выражении, получим
, а также приведя подобные члены в последнем выражении, получим 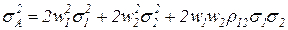 .Поскольку
.Поскольку 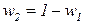 , то выражение для
, то выражение для 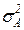 фактически зависит от одной переменной –
фактически зависит от одной переменной – 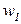 . После некоторых преобразований получим
. После некоторых преобразований получим 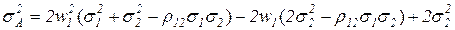 . (3.34)Мы видим, что дисперсия
. (3.34)Мы видим, что дисперсия 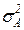 является квадратичной функцией
является квадратичной функцией 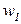 , а следовательно, и стоимости портфеля
, а следовательно, и стоимости портфеля  , которая линейно зависит от
, которая линейно зависит от 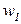 . Графически эта зависимость (ее называют границей эффективности) показана на рисунке 3.8. По смыслу граница эффективности соответствует множеству Парето при решении многокритериальных задач оптимизации, которые мы рассмотрели в разделе 2.5. В нашей задаче тоже два критерия – ожидаемая доходность и уровень риска. Используя выражение (3.34), можно найти соотношение ценных бумаг, которое обеспечит минимум риска. Для этого нужно взять производную от
. Графически эта зависимость (ее называют границей эффективности) показана на рисунке 3.8. По смыслу граница эффективности соответствует множеству Парето при решении многокритериальных задач оптимизации, которые мы рассмотрели в разделе 2.5. В нашей задаче тоже два критерия – ожидаемая доходность и уровень риска. Используя выражение (3.34), можно найти соотношение ценных бумаг, которое обеспечит минимум риска. Для этого нужно взять производную от 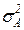 по
по 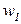 и приравнять ее к нулю. Получим:
и приравнять ее к нулю. Получим:  ,откуда оптимальное соотношение ценных бумаг определится формулами
,откуда оптимальное соотношение ценных бумаг определится формулами 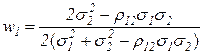 ,
, 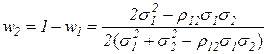 . (3.35)Подставив полученные значения весов
. (3.35)Подставив полученные значения весов 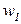 и
и 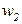 в формулы (3.33), получим параметры портфеля, обеспечивающие минимальный риск
в формулы (3.33), получим параметры портфеля, обеспечивающие минимальный риск 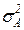 и соответствующий доход
и соответствующий доход  .При
.При  для решения подобной задачи необходимо вычислить и приравнять к нулю частные производные по всем весам
для решения подобной задачи необходимо вычислить и приравнять к нулю частные производные по всем весам 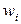 ,
, 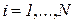 . В результате получится
. В результате получится 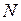 линейных уравнений относительно
линейных уравнений относительно 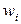 , к которым добавится еще условие (3.26). Решив эту систему, получим все веса
, к которым добавится еще условие (3.26). Решив эту систему, получим все веса 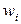 , а затем вычислим остальные параметры портфеля по приведенным выше формулам.Пример. Проиллюстрируем полученные результаты численным примером. Пусть имеется два вида ценных бумаг со следующими характеристиками:
, а затем вычислим остальные параметры портфеля по приведенным выше формулам.Пример. Проиллюстрируем полученные результаты численным примером. Пусть имеется два вида ценных бумаг со следующими характеристиками: 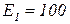 ,
, 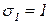 ,
, 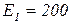 ,
, 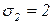 ,
, 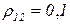 .По формулам (3.33) и (3.35) получаем:
.По формулам (3.33) и (3.35) получаем: 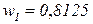 ,
,  ,
, 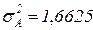 ,
, 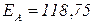 . График зависимости
. График зависимости 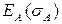 приведен на рисунке 3.8, его шутливо называют «пуля Марковица».На рисунке жирной линией выделена граница эффективности портфеля, которая располагается в диапазоне от
приведен на рисунке 3.8, его шутливо называют «пуля Марковица».На рисунке жирной линией выделена граница эффективности портфеля, которая располагается в диапазоне от  (что соответствует
(что соответствует 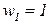 ,
, 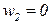 ) до
) до 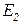 (что соответствует
(что соответствует 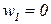 ,
, 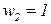 ).Мы видим, что в данном примере оптимальным с точки зрения риска является портфель, где преобладают ценные бумаги первого вида, хоть при этом ожидаемая доходность невелика.
).Мы видим, что в данном примере оптимальным с точки зрения риска является портфель, где преобладают ценные бумаги первого вида, хоть при этом ожидаемая доходность невелика.  Рисунок 3.8 Зависимость дохода от
Рисунок 3.8 Зависимость дохода от 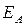 степени риска
степени риска 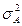
для эффективного портфеля В том случае, когда нужно решить третью из отмеченных задач, необходимо провести вертикальную линию из точки на оси абсцисс, соответствующей заданной дисперсии,
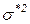 и найти наиболее высокую точку
и найти наиболее высокую точку  на границе эффективности. Соответствующий пример также показан на рисунке.
на границе эффективности. Соответствующий пример также показан на рисунке. 3.6 Имитационное моделирование при принятии решений
В дополнение к рассмотренному ранее материалу мы обратимся еще к одному методу, который позволяет не только составлять математические модели процессов, но и проводить с ними вычислительные эксперименты. Системы, осуществляющие такие функции, называются имитационными.
В настоящее время разработано и используется множество систем, реализующих методы имитационного моделирования. Одной из современных систем подобного типа является система AnyLogic, которая была разработана в 1999 году фирмой «XJ Technologies», г. Санкт-Петербург (http://www.xjtek.ru/company/) и завоевала большую популярность. К сегодняшнему дню существует уже 6 версий этой программы.
В настоящем разделе приведены краткие сведения об AnyLogic 5-й версии [5] и пример моделирования с помощью этой системы процесса прохождения студентами учебного курса.
В системе AnyLogic предусмотрены две фазы имитационного моделирования – разработка модели и ее анализ, которые явно разделены. Разработка модели выполняется в среде редактора AnyLogic, анализ модели происходит в среде исполнения. В каждой фазе существуют свои средства управления. Можно многократно использовать переход между фазами редактирования и исполнения модели при разработке модели.
Рассмотрим особенности данной системы.
3.6.1 Система AnyLogic: активные объекты, классы и экземпляры активных объектов
Система AnyLogic использует объектно-ориентированную методологию, программирования, в которой класс является мощным средством, позволяющим структурировать сложную систему. Класс определяет шаблон, в соответствии с которым строятся отдельные экземпляры класса. Эти экземпляры могут быть определены как объекты других активных объектов.
В AnyLogic основным структурным блоком при создании моделей являются классы активных объектов.Использование активных объектов является естественным средством структуризации модели сложных систем: мир состоит из множества параллельно функционирующих и взаимодействующих между собой сущностей. Различные типы этих сущностей и представляют разные активные объекты.
Чтобы создать модель AnyLogic, нужно создать классы активных объектов (или использовать объекты библиотек AnyLogic). Определение активного объекта задает шаблон. Отдельные объекты, построенные в соответствии с этим шаблоном (экземпляры активного объекта), могут использоваться затем как элементы других активных объектов. Всегда один класс в модели является корневым. Для него в модели AnyLogic порождается один экземпляр с предопределенным именем root, он и запускается исполнительной системой AnyLogic на выполнение. Имя класса корневого активного объекта можно менять в окне его свойств.
Каждый активный объект имеет структуру(совокупность включенных в него активных объектов и их связи), а также поведение, определяемое совокупностью переменных, параметров, стейтчартов (карт состояния) и т. п. Каждый экземпляр активного объекта в работающей модели имеет свое собственное поведение, он может иметь свои значения параметров, функционирует независимо от других объектов, взаимодействуя с ними и с внешней средой.
3.6.2 Объектно-ориентированный подход
AnyLogic использует объектно-ориентированный подход к представлению сложных систем. Этот подход позволяет простым и естественным образом организовать и представить структуру сложной системы с помощью иерархии абстракций. Иерархия структуры может быть произвольной глубины.
При построении моделей чаще всего не используется никаких других средств, кроме средств визуальной разработки (введения состояний и переходов карты состояний (стейтчарт – StateChart), введения пиктограмм переменных и т.п.), задания численных значений параметров, аналитических записей соотношений переменных и аналитических записей условий наступления событий. Основной парадигмой, принятой в AnyLogic при разработке моделей, является визуальное проектирование – построение с помощью графических объектов и пиктограмм иерархий структуры и поведения активных объектов.
Дата добавления: 2015-09-07; просмотров: 1166;
