Задания для самостоятельной работы 2 страница
t1 t1 t2 t3, t1 t1 t2 t4, t1 t2 t1 t1, ...}
Здесь l - пустой символ, соответствующий начальной маркировке 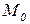 .
.
4.1.4 Основные свойства сетей Петри
Исходя из практических задач моделирования, можно установить ряд свойств сетей Петри, характеризующих поведение моделируемых систем.
Свойство ограниченности. Позиция 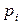 в сети P
в сети P 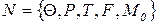 называется ограниченной, если для любой достижимой в сети маркировки M существует такое k, что
называется ограниченной, если для любой достижимой в сети маркировки M существует такое k, что 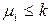 . Сеть PN называется ограниченной, если все ее позиции ограничены. Сеть, показанная на рисунке 4.1, не ограничена, т.к. возможен неограниченный рост
. Сеть PN называется ограниченной, если все ее позиции ограничены. Сеть, показанная на рисунке 4.1, не ограничена, т.к. возможен неограниченный рост 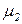 . Для обозначения неограниченной маркировки используется специальный символ w. Так, на дереве маркировок на рисунке 4.2 можно выделить маркировку
. Для обозначения неограниченной маркировки используется специальный символ w. Так, на дереве маркировок на рисунке 4.2 можно выделить маркировку 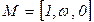 .
.
Свойство безопасности. Сеть PN называется безопасной, если при любой достижимой маркировке 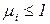 для всех
для всех 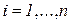 . Таким образом, в безопасной сети вектор маркировок состоит только из нулей и единиц (является двоичным словом).
. Таким образом, в безопасной сети вектор маркировок состоит только из нулей и единиц (является двоичным словом).
Свойство консервативности. Сеть называется консервативной, если сумма фишек во всех позициях остается постоянной при работе сети:
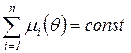 ,
, 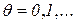 .
.
Свойство живости. Рассмотрим теперь свойства переходов. Переход 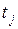 в сети
в сети 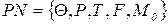 называется потенциально живым, если существует достижимая из M0 маркировка
называется потенциально живым, если существует достижимая из M0 маркировка 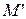 , при которой
, при которой 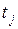 может сработать. Если
может сработать. Если 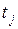 является потенциально живым при любой достижимой в
является потенциально живым при любой достижимой в 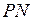 маркировке, то он называется живым. Переход
маркировке, то он называется живым. Переход 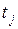 не являющийся потенциально живым при начальной маркировке M0, называется мертвым при этой маркировке. маркировка M0 в этом случае называется
не являющийся потенциально живым при начальной маркировке M0, называется мертвым при этой маркировке. маркировка M0 в этом случае называется 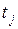 - тупиковой. Если маркировка M0 является
- тупиковой. Если маркировка M0 является 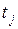 - тупиковой для всех
- тупиковой для всех 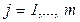 , то она называется тупиковой. При тупиковой маркировке не может сработать ни один переход. На дереве маркировок тупиковая маркировка является листом.
, то она называется тупиковой. При тупиковой маркировке не может сработать ни один переход. На дереве маркировок тупиковая маркировка является листом.
Переход называется устойчивым, если никакой другой переход не может лишить его возможности сработать при наличии для этого необходимых условий.
Последовательность маркировок 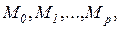 в которой
в которой 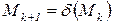 ,
, 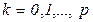 образует цикл, если
образует цикл, если 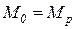 . Каждому циклу соответствует последовательность слов свободного языка сети Петри.
. Каждому циклу соответствует последовательность слов свободного языка сети Петри.
4.1.5 Некоторые обобщения сетей Петри
Рассмотренное в разделах 4.1.1 – 4.1.3 базовое определение сети Петри позволяет моделировать широкий класс дискретных систем. Однако в ряде случаев этих возможностей оказывается недостаточно, поэтому вводят обобщения этих сетей, которые обладают расширенными возможностями моделирования. Упомянем некоторые из них.
Ингибиторные сети (ИСП, IPN) – это сети Петри, для которых функция инцидентности имеет вид 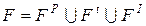 , т.е. она дополнена специальной функцией инцидентности
, т.е. она дополнена специальной функцией инцидентности 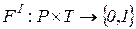 , которая вводит ингибиторные дуги для тех пар
, которая вводит ингибиторные дуги для тех пар 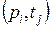 , для которых
, для которых 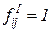 . Ингибиторные дуги связывают только позиции с переходами, эти дуги на рисунках заканчиваются не стрелками, а кружочками (рисунок 4.3). Кратность этих дуг всегда равна 1.
. Ингибиторные дуги связывают только позиции с переходами, эти дуги на рисунках заканчиваются не стрелками, а кружочками (рисунок 4.3). Кратность этих дуг всегда равна 1.
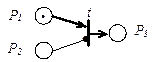
рис. 4.3. Фрагмент СП с ингибиторной дугой
Правила срабатывания переходов в ингибиторной сети модифицируются следующим образом. Переход 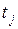 может сработать при маркировке M, если для всех связанных с ним позиций
может сработать при маркировке M, если для всех связанных с ним позиций 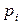 и
и 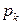
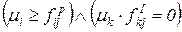 , (4.9)
, (4.9)
т.е. по сравнению с условием (4.6) введено дополнительное условие: позиция 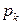 , соединенная с переходом
, соединенная с переходом 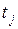 ингибиторной дугой, не должна содержать фишек (должна иметь нулевую маркировку). Так, переход t на рисунке 4.3 может срабатывать только при
ингибиторной дугой, не должна содержать фишек (должна иметь нулевую маркировку). Так, переход t на рисунке 4.3 может срабатывать только при 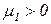 и
и 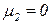 .
.
Сети с приоритетами. при определении сети Петри отмечалась недетерминированность ее работы: если имеется возможность срабатывания нескольких переходов, то срабатывает любой из них. При моделировании реальных систем могут сложиться ситуации, когда последовательность срабатываний необходимо регламентировать. Это можно сделать, введя множество приоритетов 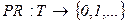 и приписав каждому из переходов
и приписав каждому из переходов 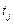 соответствующее целочисленное значение приоритета
соответствующее целочисленное значение приоритета 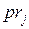 . Тогда правило срабатывания переходов модифицируется: если на некотором такте работы сети
. Тогда правило срабатывания переходов модифицируется: если на некотором такте работы сети 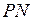 имеется возможность для срабатывания нескольких переходов, то срабатывает тот из них, который имеет наивысший приоритет. Так, из двух готовых к срабатыванию переходов
имеется возможность для срабатывания нескольких переходов, то срабатывает тот из них, который имеет наивысший приоритет. Так, из двух готовых к срабатыванию переходов 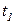 и
и 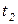 на рисунке 4.4 а первым должен сработать переход
на рисунке 4.4 а первым должен сработать переход 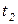 , имеющий приоритет
, имеющий приоритет 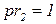 , поскольку приоритет перехода
, поскольку приоритет перехода 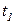
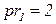 , т.е. ниже.
, т.е. ниже.

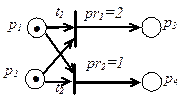
а) б)
Рис. 4.4. Сеть Петри с заданными приоритетами (а), эквивалентная цепь Маркова при вероятностном срабатывании переходов (б)
Сети со случайными срабатываниями переходов. В описанной выше ситуации, когда имеется возможность срабатывания нескольких переходов 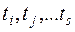 , их приоритет можно задавать вероятностями срабатывания каждого их переходов
, их приоритет можно задавать вероятностями срабатывания каждого их переходов 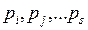 , причем
, причем 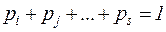 . Тогда исходная маркировка
. Тогда исходная маркировка 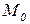 приведет на следующих шагах работы сети к набору маркировок
приведет на следующих шагах работы сети к набору маркировок 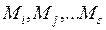 , каждая из которых будет помечена соответствующей вероятностью. Отождествив маркировки с состоянием сети и положив, что вероятности не зависят от работы сети в предыдущие такты, мы получим цепь Маркова, описывающую вероятностное поведение системы (см. главу 3).
, каждая из которых будет помечена соответствующей вероятностью. Отождествив маркировки с состоянием сети и положив, что вероятности не зависят от работы сети в предыдущие такты, мы получим цепь Маркова, описывающую вероятностное поведение системы (см. главу 3).
Пусть на рисунке 4.4 а вероятность срабатывания перехода 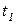 равна p, а вероятность срабатывания
равна p, а вероятность срабатывания 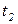 равна
равна 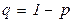 . Тогда обозначив маркировки
. Тогда обозначив маркировки 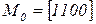 ,
, 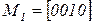 ,
, 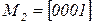 , получим цепь Маркова (рисунок 4.4 б).
, получим цепь Маркова (рисунок 4.4 б).
Иерархические сети Петри представляют собой многоуровневые структуры, в которых выделяются сети различного уровня. Они позволяют моделировать различные многоуровневые (иерархические) системы.
В отличие от обыкновенных сетей Петри, в иерархических сетях имеются два типа переходов: простые и составные. Простые переходы ничем не отличаются от рассмотренных ранее, а составные переходы содержат внутри себя сеть Петри более низкого уровня. Формально они состоят из входного («головного») и выходного («хвостового») переходов, между ними находится некоторая сеть Петри, которая, в свою очередь, также может быть иерархической.
Пример иерархической сети 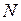 , в которой имеется составной переход
, в которой имеется составной переход 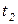 , содержащий внутри себя сеть
, содержащий внутри себя сеть 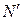 , показан на рисунке 4.5. Составной переход
, показан на рисунке 4.5. Составной переход 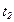 имеет «голову»
имеет «голову» 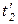 и «хвост»
и «хвост» 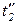 , между которыми заключена сеть
, между которыми заключена сеть 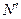 , состоящая из позиций
, состоящая из позиций 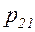 -
- 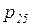 и переходов
и переходов 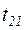 -
- 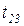 .
.
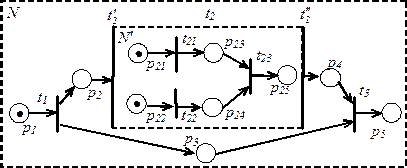
Рис. 4.5. Иерархическая сеть Петри
Иерархическая сеть функционирует, как и обыкновенная СП, переходя от одной маркировки к другой и обмениваясь фишками (в том числе между сетями различного уровня). Исключение составляют правила работы составных переходов.
Срабатывание составных переходов является не единовременным событием, как в обыкновенных СП, а составным действием. Поэтому говорят не о срабатывании составного перехода, а о его работе. На каждом шаге дискретного времени 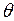 составной переход может находиться в одном из двух состояний – пассивном и активном. Начальное состояние всех переходов – пассивное. Составной переход может быть активирован, в момент времени
составной переход может находиться в одном из двух состояний – пассивном и активном. Начальное состояние всех переходов – пассивное. Составной переход может быть активирован, в момент времени 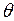 , если он до этого был пассивен и имеются условия для срабатывания его головного перехода, задаваемые условиями (4.6). При этом производится изменение маркировки в сети верхнего уровня по обычным правилам (4.7) и одновременно запускается работа в сети, находящейся внутри составного перехода. Во время ее работы функционирование сети верхнего уровня блокируется. Сеть нижнего уровня работает с учетом своей начальной маркировки до тех пор, пока все ее переходы не станут пассивными (т.е. не смогут сработать). После этого происходит срабатывание хвостового перехода и изменение маркировки сети верхнего уровня согласно (4.7). Составной переход возвращается в пассивное состояние, а в сети нижнего уровня восстанавливается начальная маркировка.
, если он до этого был пассивен и имеются условия для срабатывания его головного перехода, задаваемые условиями (4.6). При этом производится изменение маркировки в сети верхнего уровня по обычным правилам (4.7) и одновременно запускается работа в сети, находящейся внутри составного перехода. Во время ее работы функционирование сети верхнего уровня блокируется. Сеть нижнего уровня работает с учетом своей начальной маркировки до тех пор, пока все ее переходы не станут пассивными (т.е. не смогут сработать). После этого происходит срабатывание хвостового перехода и изменение маркировки сети верхнего уровня согласно (4.7). Составной переход возвращается в пассивное состояние, а в сети нижнего уровня восстанавливается начальная маркировка.
Ниже приведено дерево маркировок сетей 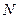 и
и 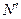 при указанных на рисунке 4.5 начальных маркировках (рисунок 4.6).
при указанных на рисунке 4.5 начальных маркировках (рисунок 4.6).
Мы видим, что на шаге 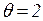 происходит работа составного перехода
происходит работа составного перехода 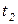 и сети
и сети 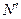 в следующем порядке: срабатывание
в следующем порядке: срабатывание 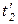 - запуск
- запуск 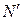 - окончание работы
- окончание работы 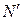 и восстановление ее начальной маркировки – срабатывание
и восстановление ее начальной маркировки – срабатывание 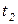 и продолжение работы сети
и продолжение работы сети 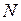 .
.
Отметим также, что описанный процесс напоминает выполнение подпрограммы при программировании на алгоритмических языках. Срабатывание перехода 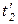 соответствует вызову подпрограммы, а срабатывание
соответствует вызову подпрограммы, а срабатывание 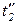 - возврату в основную программу.
- возврату в основную программу.
Рис. 4.6. Схема работы иерархической сети Петри
Раскрашенные (цветные) сети Петри (РСП, CPN - Colored Petri Nets). В ряде приложений перемещаемые в сети Петри ресурсы (фишки) требуется дифференцировать, и тогда приходится вводить фишки различных видов (например, разных цветов). В этом случае для каждого перехода необходимо указывать, при каких комбинациях фишек во входных позициях он может сработать, и какое количество фишек различных цветов помещается в выходные позиции.
Понятно, что моделирующая возможность раскрашенных сетей Петри выше, чем у обычных, однако при этом значительно усложняется их описание.
Формальное определение и подробное описание работы раскрашенных сетей Петри приведено в разделе 4.2.
Следует отметить, что раскрашенные сети Петри могут быть преобразованы в обычные, но при этом возрастают размеры сети.
Упомянем еще некоторые расширения сетей Петри: синхронные, самомодифицируемые (с изменяющейся кратностью дуг, когда матрицы 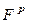 и
и 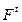 зависят от t), и другие, описанные в литературе [18, 28].
зависят от t), и другие, описанные в литературе [18, 28].
Инварианты сетей Петри
Структура сетей Петри может обеспечивать при работе сети постоянство некоторых функций от маркировок сети. Такие функции называют инвариантами сетей Петри. Вычисление инвариантов может оказаться полезным при исследовании свойств моделируемых систем (например, при верификации и тестировании программ, анализе бизнес-процессов и др.) [11, 42].
Различают инварианты позиций и инварианты переходов.
Для того, чтобы пояснить смысл этих терминов, введем в рассмотрение 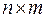 -матрицу
-матрицу
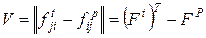 ,
,
каждый элемент которой 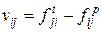 показывает разность между числом поступивших фишек –
показывает разность между числом поступивших фишек – 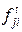 и числом изъятых
и числом изъятых 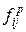 , т.е. изменение маркировки позиции
, т.е. изменение маркировки позиции 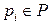 при срабатывании перехода
при срабатывании перехода 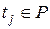 . В силу того, что
. В силу того, что 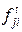 и
и 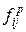 –целые числа, величины
–целые числа, величины 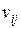 также целые. В зависимости от знака
также целые. В зависимости от знака 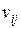 при срабатывании перехода
при срабатывании перехода 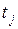 в позиции
в позиции 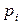 число фишек либо увеличивается (
число фишек либо увеличивается ( 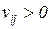 ), либо уменьшается (
), либо уменьшается ( 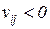 ), либо остается неизменным (
), либо остается неизменным ( 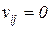 ).
).
1. Инварианты позиций. Припишем каждой позиции 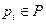 некоторый вес
некоторый вес  , который может принимать целочисленные значения – положительные, отрицательные или нулевые. Эти веса образуют
, который может принимать целочисленные значения – положительные, отрицательные или нулевые. Эти веса образуют 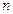 -вектор-строку
-вектор-строку
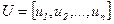 .
.
Рассмотрим 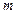 -вектор-строку
-вектор-строку 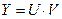 и определим условия, при которых этот вектор является нулевым, т.е.
и определим условия, при которых этот вектор является нулевым, т.е.
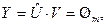 (4.10)
(4.10)
где 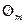 -
- 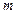 -вектор-строка, состоящая из нулей,
-вектор-строка, состоящая из нулей, 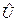 - ненулевой
- ненулевой 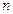 -вектор.
-вектор.
Представим матрицу 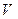 в виде
в виде 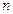 -столбца:
-столбца:
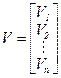 ,
,
где 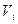 -вектор-строка. Тогда условие (4.10) может быть представлено в виде
-вектор-строка. Тогда условие (4.10) может быть представлено в виде
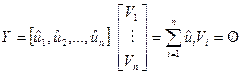 .
.
Отсюда следует, что условие (2.8) при 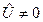 может выполняться только в том случае, если среди строк
может выполняться только в том случае, если среди строк 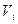 матрицы
матрицы 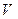 найдутся линейно зависимые строки, т.е. дефект матрицы
найдутся линейно зависимые строки, т.е. дефект матрицы 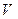 был бы больше нуля:
был бы больше нуля: 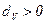 .
.
Пусть для простоты имеются две такие строки с номерами 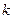 и
и 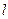 -
- 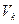 и
и 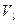 , которые соответствуют в матрице
, которые соответствуют в матрице 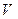 позициям
позициям 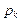 и
и 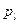 , и пусть соответствующие веса не равны нулю:
, и пусть соответствующие веса не равны нулю: 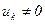 ,
, 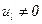 . Веса остальных позиций положим равными нулю:
. Веса остальных позиций положим равными нулю: 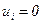 при
при 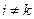 ,
, 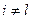 . В силу линейной зависимости строк
. В силу линейной зависимости строк 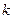 и
и 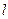 веса
веса 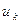 и
и 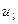 можно подобрать таким образом, что
можно подобрать таким образом, что
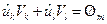 ;
; 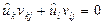 ,
, 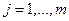 . (4.11)
. (4.11)
Таким образом, вектор 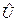 имеет вид
имеет вид
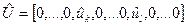
и в силу (4.11) обеспечивается выполнение условия (4.10).
Подсчитаем теперь приращение числа фишек в позициях 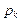 и
и 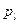 при срабатывании перехода
при срабатывании перехода 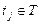 . Пусть до срабатывания перехода
. Пусть до срабатывания перехода 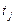 маркировки в позициях
маркировки в позициях 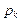 и
и 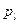 были соответственно
были соответственно 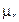 и
и 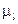 . После срабатывания
. После срабатывания 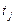 маркировки с учетом введенных весов
маркировки с учетом введенных весов 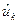 и
и 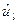 стали равными,
стали равными, 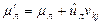 ,
, 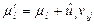 , а их сумма
, а их сумма 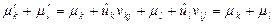 в силу (4.11).
в силу (4.11).
Таким образом, сумма 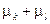 при учете введенных весов позиций
при учете введенных весов позиций 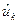 ,
, 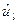 остается постоянной при срабатывании любого перехода и равна этой сумме при начальной маркировке
остается постоянной при срабатывании любого перехода и равна этой сумме при начальной маркировке 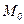 .
.
Построенный описанным образом вектор 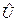 называется инвариантом позиций сети Петри.
называется инвариантом позиций сети Петри.
2. Инварианты переходов. По аналогии с предыдущим разделом припишем каждому переходу 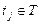 вес
вес 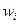 , который может принимать целочисленные значения любого знака. Эти веса сведем в
, который может принимать целочисленные значения любого знака. Эти веса сведем в 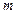 -вектор-столбец
-вектор-столбец
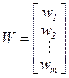 .
.
Рассмотрим 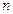 -вектор-столбец
-вектор-столбец 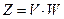 и определим условия, при которых этот вектор является нулевым, т.е.
и определим условия, при которых этот вектор является нулевым, т.е.
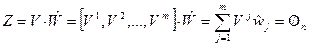 , (4.12)
, (4.12)
где 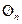 -
- 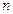 -вектор=столбец, состоящий из нулей,
-вектор=столбец, состоящий из нулей, 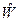 - ненулевой
- ненулевой 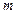 ‑вектор,
‑вектор, 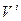 -
- 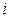 -й
-й 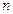 - столбец матрицы
- столбец матрицы 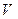 .
.
Аналогично сказанному выше, можно убедиться в том, что условие (4.12) выполняется только в том случае, когда среди столбцов матрицы 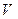 найдутся линейно зависимые. Для этого необходимо, как было показано, чтобы дефект матрицы
найдутся линейно зависимые. Для этого необходимо, как было показано, чтобы дефект матрицы 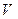 был бы больше нуля:
был бы больше нуля: 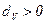 . Пусть имеются два линейно зависимых столбца с номерами
. Пусть имеются два линейно зависимых столбца с номерами 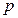 и
и 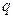 , которые соответствуют переходам
, которые соответствуют переходам 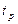 и
и 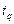 , и пусть соответствующие веса не равны нулю,
, и пусть соответствующие веса не равны нулю, 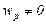 ,
, 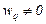 . Остальные веса положим нулевыми:
. Остальные веса положим нулевыми: 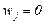 при
при 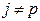 ,
, 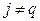 . В силу линейной зависимости векторов
. В силу линейной зависимости векторов 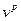 и
и 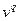 можно подобрать веса
можно подобрать веса 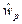 и
и 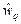 таким образом, чтобы выполнялось условие (2.10).
таким образом, чтобы выполнялось условие (2.10).
Проанализируем теперь, как будет изменяться маркировка сети при последовательном срабатывании переходов 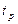 и
и 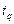 . Пусть маркировка некоторой позиции
. Пусть маркировка некоторой позиции 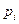 до срабатывания переходов была
до срабатывания переходов была 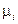 . После срабатывания
. После срабатывания 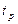 она (с учетом веса,
она (с учетом веса, 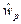 ) стала
) стала 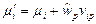 а после срабатывания
а после срабатывания 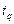 (с учетом веса
(с учетом веса 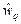 )
) 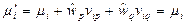 . Таким образом, после последнего срабатывания переходов
. Таким образом, после последнего срабатывания переходов 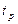 и
и 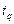 получается исходная маркировка всех позиций,
получается исходная маркировка всех позиций, 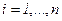 .
.
Дата добавления: 2015-09-07; просмотров: 2039;
