Задания для самостоятельной работы 5 страница
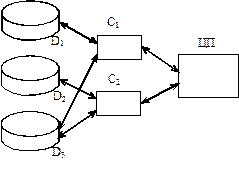
рис. 4.14. Схема ВС с альтернативными ресурсами
Обыкновенная сеть Петри PN для моделирования этой системы показана на рисунке 4.15.
Позиции pd1 , pd2 , pd3 определяют, свободен или занят соответствующий дисковод D1, D2, D3 , позиции pc1, pc2, соответственно - свободен или занят соответствующий канал С1 и С2. Позиции p1 и p2 - выполнение заданий парами D1C1 и D2C2, позиции p31 и p32 - выполнение задания парами D3 C1 и D3C2.

рис. 4.15. Обыкновенная сеть Петри,
моделирующая систему на рисунке 4.145
Каждый из переходов 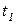 ,
, 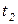 ,
, 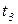 ,
, 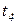 при срабатывании определяет один из четырех возможных вариантов обслуживания задания. При построении дерева маркировок необходимо дать возможность сработать каждому из них.
при срабатывании определяет один из четырех возможных вариантов обслуживания задания. При построении дерева маркировок необходимо дать возможность сработать каждому из них.
переходы 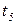 ,
, 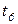 ,
, 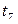 ,
, 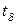 моделируют завершение выполнения задания по каждому из рассмотренных вариантов.
моделируют завершение выполнения задания по каждому из рассмотренных вариантов.
Рассмотренную сеть можно значительно упростить, если использовать формализм раскрашенных сетей Петри CPN. В этом случае она примет вид, показанный на рисунке 4.16.
рис. 4.16. Раскрашенная сеть Петри,
моделирующая систему на рисунке 4.14
Здесь позиция pd определяет наличие свободных дисководов, а позиция pc – наличие свободных каналов. Введем графическое и буквенное обозначение ресурсов, используемых в данной сети
° ‑ (d1); * ‑ (d2); + ‑ (d3) – свободные дисководы
´ ‑ (c1); Ä ‑ (c2) – свободные каналы
·‑ e – поступившие/выполненные заявки.
кроме того, необходимо ввести дополнительные фишки для запоминания предыдущих состояний сети (на рисунке не указаны)
m1 – занят дисковод D1 и канал C1
m2 – занят дисковод D2 и канал C2
m3 – занят дисковод D3 и канал C1
m4 – занят дисковод D3 и канал C2
правила срабатывания переходов t1, t2, t3 задаются следующими таблицами.
Таблица 4.1
| Переход t1 | Переход t2 | Переход t3 | ||||||||
| p0 | pd | p1 | p1 | pc | p2 | p2 | p3 | pc | pd | |
| e | d1 | d1 | d1 | c1 | m1 | m1 | e | c1 | d1 | |
| e | d2 | d2 | d2 | c2 | m2 | m2 | e | c2 | d2 | |
| e | d3 | d3 | d3 | c1 | m3 | m3 | e | c1 | d3 | |
| d3 | c2 | m4 | m4 | e | c2 | d3 | ||||
Приведем теперь формальное описание данной CPN в нотации К. Йенсена (см. п. 4.2).
· Множества цветов:
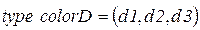 ;
;
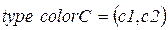 ;
;
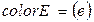 ;
;
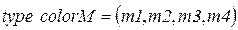 .
.
· Цветовые переменные:
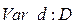 ;
; 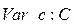 ;
; 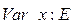 ;
; 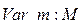 .
.
· Множество позиций:
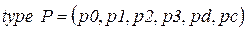 ;
;
переменная типа позиции:
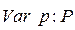 .
.
· Множество переходов:
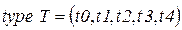 ;
;
переменная типа перехода:
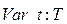 .
.
· Множество дуг 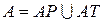 ;
;
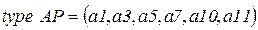 ;
;
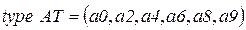 ;
;
переменные типа дуги:
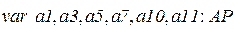 ;
;
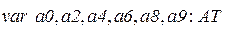 ,
,
где типы 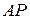 и
и 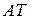 описаны выражениями в соответствии с примером (4.19).
описаны выражениями в соответствии с примером (4.19).
· Цветовая функция
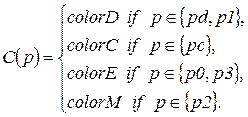
· Блокировочная функция отсутствует, т.е. формально определяется выражениями:
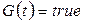 ,
, 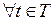 .
.
· функция инициализации 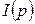 , задающая начальную маркировку
, задающая начальную маркировку 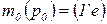 ;
; 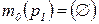 ;
; 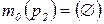 ;
; 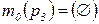 ;
; 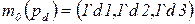 ;
; 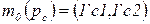
· выражения на дугах 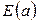 приведены в таблице 4.2.
приведены в таблице 4.2.
Таблица 4.2
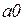
| 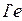
|
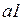
| 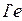
|
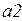
| 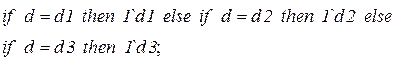
|
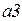
| 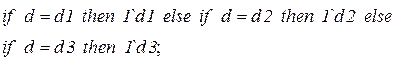
|
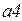
| 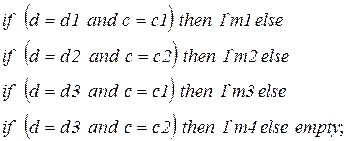
|
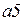
| 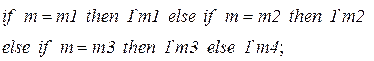
|
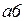
| 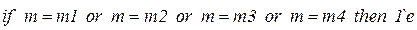
|
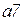
| 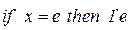
|
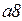
| 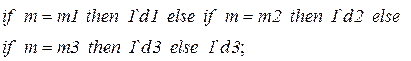
|
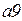
| 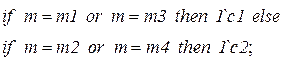
|
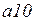
| 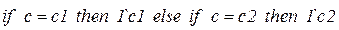
|
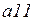
| 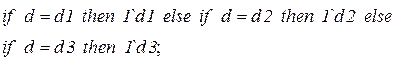
|
Предлагаем читателю самостоятельно проследить схему изменения маркировок при обслуживании поступивших заданий по всем четырем возможным вариантам.
5. Задача об обедающих мудрецах.Моделирование систем с помощью сетей Петри особенно полезно в тех случаях, когда компоненты систем могут взаимодействовать в процессе работы системы. Управление взаимодействующими процессами называют синхронизацией.
Имеется ряд классических задач в этой области: о взаимном исключении, производитель/потребитель, чтения/записи, об обедающих мудрецах. Последнюю рассмотрим подробнее.
Эта задача была предложена Э. Дейкстрой в 1968 году в статье о параллельных вычислениях, где он впервые ввел понятие «семафора» [9]. С тех пор она служит своеобразным тестом для методов решения задач распараллеливания.
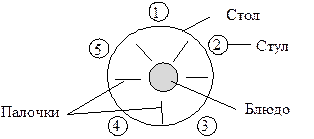
Рис. 4.17. Столовая гуляющих мудрецов
Имеется 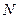 китайских мудрецов, которые то гуляют по парку, то обедают. Каждый из них действует совершенно независимо. Проголодавшись, он идет в столовую, садится на свободный стул за круглый стол, на котором стоит блюдо с рисом, берет две палочки и обедает. Но палочек всего
китайских мудрецов, которые то гуляют по парку, то обедают. Каждый из них действует совершенно независимо. Проголодавшись, он идет в столовую, садится на свободный стул за круглый стол, на котором стоит блюдо с рисом, берет две палочки и обедает. Но палочек всего 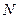 . Если свободных палочек нет, то мудрец ждет, когда освободятся соседние палочки. Насытившись, он кладет палочки на место и уходит. На рисунке 4.17 показана схема столовой для
. Если свободных палочек нет, то мудрец ждет, когда освободятся соседние палочки. Насытившись, он кладет палочки на место и уходит. На рисунке 4.17 показана схема столовой для 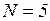 . Обозначим состояния, относящиеся к произвольному i-му мудрецу (
. Обозначим состояния, относящиеся к произвольному i-му мудрецу ( 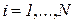 ):
):
Mi – i-ый мудрец гуляет;
Еi – i-ый мудрец ест;
Ck – k-ая палочка свободна;
С1i – i-ый мудрец держит левую палочку;
C2i – i-ый мудрец держит правую палочку.
Рассмотрим возможные события:
ti1 – мудрец начинает есть;
ti2 – мудрец уходит гулять и освобождает палочки;
ti3 – мудрец взял левую палочку;
ti4 – мудрец взял правую палочку.
Тогда для отдельного i-го мудреца имеем обыкновенную сеть Петри (рисунок 4.18).
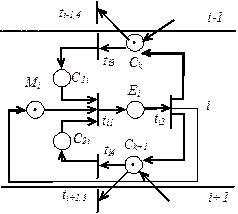
рис. 4.18. Сеть Петри, моделирующая поведение одного мудреца
Из рисунка видно, что мудрецы взаимно связаны орудиями питания, т.е. из-за ресурса Ck (палочек) имеется конкуренция.
В соответствии с расположением мест за обеденным столом (рисунок 4.17), сети Петри для 1-го и 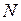 -го мудрецов должны соединяться. При нумерации мест по часовой стрелке правая палочка 1-го мудреца является левой для
-го мудрецов должны соединяться. При нумерации мест по часовой стрелке правая палочка 1-го мудреца является левой для 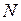 -го. Таким образом, полный граф
-го. Таким образом, полный граф 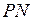 для данного примера представляет собой кольцо, образованное сетями для отдельных мудрецов.
для данного примера представляет собой кольцо, образованное сетями для отдельных мудрецов.
Среди всевозможных маркировок данной сети Петри существуют тупиковые - когда все мудрецы сидят за столом и взяли в руки по одной палочке (например, правой). В этом случае они обречены на голодную смерть, т.к. они никогда не дождутся второй палочки и не смогут начать обед. Этот модельный пример свидетельствует о том, что в реальных параллельно работающих системах должен быть механизм синхронизации, способный разрешить подобные конфликты.
Задача о мудрецах может быть смоделирована с помощью раскрашенных сетей Петри. Эта задача предлагается в качестве одного из заданий самостоятельной работы.
4.3.2 моделирование программ
Напомним некоторые определения, относящиеся к теории программирования. Моделью программирования называют совокупность приемов программирования и структур данных, отвечающих архитектуре используемого компьютера и предназначенных для выполнения определенного класса алгоритмов. Описание алгоритма является иерархическим, его сложность зависит от степени детализации. На самом верхнем уровне иерархии находится задача в целом, нижний уровень включает примитивные операции – машинные команды. Алгоритм можно представить в виде диаграммы – информационного графа, который описывает последовательность выполнения операций и взаимную зависимость между различными операциями или блоками операций. Узлами информационного графа являются операции, а однонаправленными дугами – каналы обмена данными.
Традиционной считается последовательная модель программирования. В этом случае в любой момент времени выполняется только одна операция и только над одним элементом данных. Эта модель характеризуется возможностью применения стандартных языков программирования, хорошей переносимостью программ и невысокой производительностью.
В более поздних вычислительных системах получила развитие идея распараллеливания вычислений, которая воплотилась в архитектуре практически всех современных компьютеров. В связи с этим появились модели параллельного программирования. Их особенностями являются более высокая производительность программ, применение специальных приемов программирования и, как следствие, более высокая трудоемкость программирования и проблемы с переносимостью программ.
Простейшая модель параллельного программирования называется моделью задача/канал. В этом случае программа состоит из нескольких задач, связанных между собой каналами телекоммуникаций и выполняемых одновременно несколькими процессорами. Каждая задача состоит из последовательного кода и локальной памяти. Канал – это очередь сообщений, передающих данные от одной задачи к другой. Каждая задача может записывать и считывать данные из локальной памяти, посылать и принимать сообщения. Операция обмена сообщениями может быть асинхронной, она завершается сразу после пересылки сообщения, либо синхронной, которая блокирует выполнение задачи до тех пор, пока не прейдет подтверждение получения сообщения адресатом. Другой распространенной моделью параллельного программирования является модель параллелизма данных. Она основана на применении одного и того же алгоритма несколькими процессорами к множеству элементов структуры данных (например, к фрагментам одного массива).
Обратимся теперь к описанию алгоритмов с помощью сетей Петри. Эти сети, оперируя терминами условия–события, являются удобным инструментом моделирования как структуры информационных графов программ, так и динамики выполнения программных блоков. При этом наличие данных для выполнения некоторых операций моделируется маркировкой соответствующей позиции, а сама операция моделируется срабатыванием перехода.
Ниже приводятся примеры моделей последовательной и параллельной программ, построенных средствами сетей Петри [18]. Отметим, что данный материал не претендует на изложение теории параллельных вычислений – он лишь демонстрирует моделирующие возможности сетей Петри.
Последовательная модель программирования.На рисунке 4.20 в качестве примера последовательной модели программирования показан информационный граф (стандартная блок-схема) алгоритма циклических вычислений. Здесь же приводится интерпретация этого графа в терминах обыкновенных сете Петри. Нетрудно убедиться, что сеть Петри в данном случае менее выразительна и содержит меньше информации об алгоритме, чем блок-схема, поскольку она требует дополнительного пояснения смысла позиций, переходов и фишек.
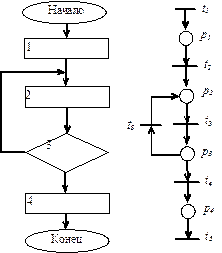
рис. 4.19. Блок-схемы алгоритма в стандартной нотации и
в виде графа сети Петри
Модель параллелизма данных.Рассмотрим теперь схему программы, соответствующую модели параллелизма данных. Предположим, что в программе имеются блоки двух типов: 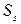 и
и  (рисунок 4.20 а). Алгоритм блока
(рисунок 4.20 а). Алгоритм блока 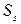 может выполняться только в последовательном режиме одним процессором, а блок
может выполняться только в последовательном режиме одним процессором, а блок 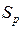 допускает разбивку на
допускает разбивку на 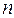 независимых модулей,
независимых модулей, 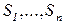 , каждый из которых может выполняться на отдельном процессоре.
, каждый из которых может выполняться на отдельном процессоре.
Сеть Петри показана на рисунке 4.20 б. Мы видим, что блок 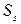 одновременно передает данные и управление модулям
одновременно передает данные и управление модулям 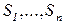 , которые являются отдельными сетями Петри (это происходит при срабатывании перехода
, которые являются отдельными сетями Петри (это происходит при срабатывании перехода 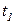 ).
).
Модули выполняются независимо, однако дальнейшие вычисления могут начаться только после завершения выполнения всех модулей (т.е. должны сложиться условия для срабатывания перехода 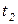 ). Таким образом, с помощью сети Петри можно описать нетривиальные особенности параллельного выполнения модулей. С помощью стандартных блок-схем это было бы сделать затруднительно.
). Таким образом, с помощью сети Петри можно описать нетривиальные особенности параллельного выполнения модулей. С помощью стандартных блок-схем это было бы сделать затруднительно.
На примере данной схемы можно вывести известную формулу Амдала, которая характеризует эффективность параллельных алгоритмов.
Пусть блок 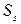 требует для своего выполнения времени
требует для своего выполнения времени 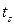 , а блок
, а блок 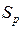 при его выполнении на одном процессоре – времени
при его выполнении на одном процессоре – времени 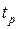 . Тогда общее время решения задачи на одном процессоре составит
. Тогда общее время решения задачи на одном процессоре составит  . Если же блок
. Если же блок 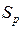 выполняется параллельно на
выполняется параллельно на 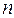 одинаковых процессорах, то время его выполнения в идеальном случае (при равномерной загрузке всех процессоров) составит
одинаковых процессорах, то время его выполнения в идеальном случае (при равномерной загрузке всех процессоров) составит 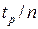 , а общее время решения задачи будет
, а общее время решения задачи будет 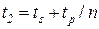 .
.
Коэффициент ускорения вычислений составит
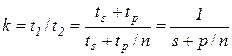 , (4.22)
, (4.22)
где 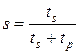 ,
, 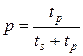 – относительные доли последовательной и параллельной частей (
– относительные доли последовательной и параллельной частей ( 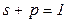 ).
).
Выражение (4.22) носит название формулы Амдала.
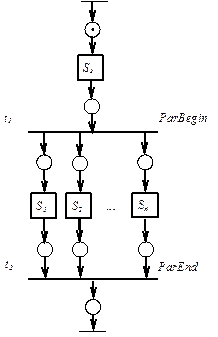
а) б)
рис. 4.20. Модель программы,
допускающей распараллеливание вычислений
Мы видим, что чем больше величина 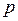 , тем больший эффект дает эффект распараллеливания вычислений. При малых
, тем больший эффект дает эффект распараллеливания вычислений. При малых 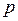 ускорение вычислений за счет увеличения числа процессоров будет незначительным. Например, при
ускорение вычислений за счет увеличения числа процессоров будет незначительным. Например, при 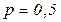 и
и 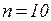 получим
получим 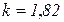 , т.е. десятикратное увеличение числа процессоров уменьшает время вычислений менее чем в 2 раза.
, т.е. десятикратное увеличение числа процессоров уменьшает время вычислений менее чем в 2 раза.
4.3.3 Моделирование протоколов передачи данных
Протоколами называют наборы правил (алгоритмы) для связи между абонентами вычислительной или телекоммуникационной системы. Протоколы управляют форматом, временными интервалами, последовательностью работы и контролем ошибок при передаче сообщений. В соответствии с принятой моделью связи открытых систем OSI (Open System Interconnection) существует семь уровней взаимодействия между абонентами системы – от физического (нижний уровень) до прикладного (верхний уровень). На каждом из уровней должен действовать свой протокол. На практике обычно используется всего три уровня протоколов:
– низший аппаратный (протоколы Ethernet, Tokeu Ring, FDDI);
– средний уровень (протоколы NetBIOS, IPX/SPX, TCP/IP);
– высший уровень (протоколы SMB, NCP).
Реальные протоколы представляют собой достаточно сложные алгоритмы, и поэтому возникает необходимость моделирования их работы с целью определения рабочих характеристик или обнаружения ошибок. Сеть Петри, моделирующая работу реального протокола, обычно содержит сотни узлов-позиций и переходов. В данной книге мы рассмотрим значительно упрощенную модель протокола передачи данных, которая, тем не менее, отражает существенные черты его работы [42].
Раскрашенная сеть Петри с временным механизмом, моделирующая работу протокола, приведена на рисунке 4.21.
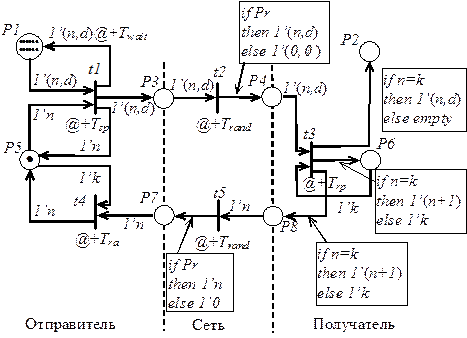
Рис. 4.21. Модель протокола передачи данных
1. Описание работы протокола. Система передачи данных, реализуемая с помощью протокола, состоит из трех подсистем: отправитель, получатель и сеть, по которой в одну сторону передается сообщение, а в обратную сторону – подтверждение о приеме сообщения получателем («квитанция»).
По сети передается сообщение, разбитое на 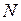 фрагментов, называемых пакетами. Каждый пакет состоит из номера (целое число типа integer с временной меткой) и текстовой части (типа string). Первоначально все
фрагментов, называемых пакетами. Каждый пакет состоит из номера (целое число типа integer с временной меткой) и текстовой части (типа string). Первоначально все 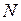 пакетов находятся в позиции
пакетов находятся в позиции 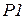 . Целью работы системы является передача всех пакетов получателю в позицию
. Целью работы системы является передача всех пакетов получателю в позицию 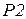 с сохранением последовательности их номеров. Кроме того, отправитель должен получить «квитанции» о передаче всех пакетов, и эти «квитанции» с пометкой о времени передачи помещаются в
с сохранением последовательности их номеров. Кроме того, отправитель должен получить «квитанции» о передаче всех пакетов, и эти «квитанции» с пометкой о времени передачи помещаются в 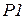 .
.
позиции 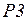 ,
, 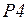 моделируют, соответственно, условия начала и конца передачи пакетов, а позиции
моделируют, соответственно, условия начала и конца передачи пакетов, а позиции  ,
, 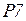 моделируют условия начала и конца передачи «квитанций».
моделируют условия начала и конца передачи «квитанций».
позиции 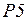 ,
, 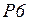 являются счетчиками, т.е. хранят номера отправленных и принятых пакетов.
являются счетчиками, т.е. хранят номера отправленных и принятых пакетов.
Переход 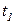 моделирует начало передачи очередного пакета, переходы
моделирует начало передачи очередного пакета, переходы 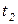 и
и 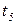 - прохождение, соответственно, пакета и «квитанции» через сеть, переход
- прохождение, соответственно, пакета и «квитанции» через сеть, переход 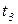 - прием и анализ очередного пакета, переход
- прием и анализ очередного пакета, переход 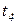 - прием и анализ очередной «квитанции».
- прием и анализ очередной «квитанции».
2. формальное описание CPN, моделирующей протокол. ниже приведено формальное описание сети на рисунке 4.21 в сокращенном виде.
· Множество цветов:
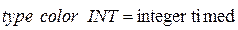 ;
;
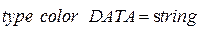 ;
;
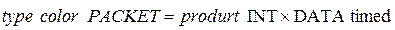 ;
;
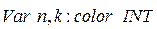 ;
; 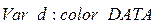 ;
;
· Множества позиций 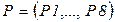 и переходов
и переходов 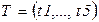 показаны непосредственно на рисунке.
показаны непосредственно на рисунке.
· Цветовая функция имеет вид
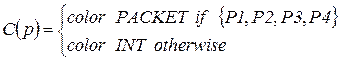
· Выражения на дугах 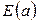 показаны непосредственно на рисунке 4.21. Обратим внимание на дуги
показаны непосредственно на рисунке 4.21. Обратим внимание на дуги 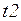 to
to 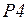 и
и 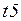 to
to 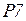 . Выражения на этих дугах зависят от датчика случайного кода
. Выражения на этих дугах зависят от датчика случайного кода 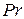 , который с определенной вероятностью вырабатывает значение true или false. Прохождение сигнала по этим дугам рассмотрено ниже.
, который с определенной вероятностью вырабатывает значение true или false. Прохождение сигнала по этим дугам рассмотрено ниже.
· функции на переходах 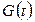 , определяющие временные задержки при срабатывании переходов, (т.е. передаче сообщений), также показаны на рисунке.
, определяющие временные задержки при срабатывании переходов, (т.е. передаче сообщений), также показаны на рисунке.
Дата добавления: 2015-09-07; просмотров: 1137;
