Задания для самостоятельной работы 6 страница

· функция инициализации имеет вид (рисунок 4.21) 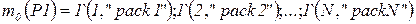- иными словами, в начальный момент времени ( 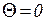, 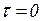) в позиции 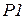находится 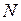подлежащих передаче пакетов, структура которых определена типом ;

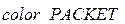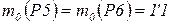- начальный номер передаваемого пакета;

.

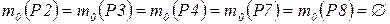3. Временной механизм работы CPN. Важную роль в работе рассматриваемой модели играет временной механизм.

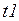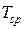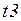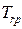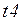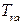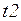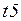
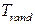Все переходы осуществляют временную задержку: - на время , - на время , - на время , задержка срабатывания переходов и является случайной величиной, которую генерирует датчик случайных чисел. На дуге 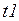to 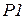введена задержка на время .

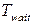Перемещаемые в сети фишки имеют временные метки, и при их прохождении через переходы значения «прикрепленного» времени возрастают, что моделирует задержку передачи как сообщений, так и «квитанций».

Помимо временной задержки, в рассматриваемой CPN моделируется потеря сообщения как при передаче пакета (на 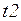to 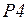), так и при передаче «квитанции» (на дуге 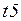to 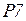). Моделирование этих событий состоит в том, что с некоторой вероятностью, генерируемой специальным датчиком 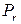, вместо очередного пакета вида 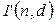по дуге 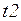to 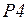передается «пустой» пакет 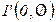, а по дуге 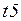to 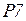вместо сообщения 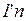– «пустое» сообщение .

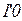4. Описание работы CPN. Проследим передачу одного пакета в системе. Пусть часы глобального времени в момент начала передачи показывают 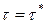. В позиции 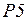находится фишка 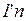, в позиции 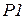- фишки 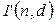,…, , 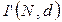а в позиции 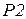- фишки 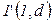,…, , 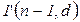где 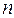-номер очередного передаваемого пакета, .

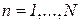При срабатывании 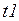из 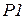извлекается фишка 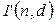и с задержкой 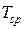передается в 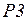. Кроме того, фишка 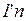с задержкой 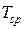по дуге 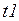to 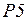возвращается в 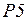, а фишка 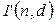по дуге 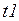to 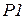с временной меткой 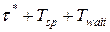направляется в .

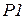Следующим срабатывает переход 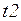и со случайной задержкой 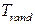передает в 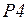либо фишку 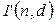, либо «пустою» 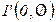- в зависимости от сигнала датчика 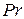. Переход 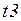анализирует пришедшую в 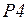информацию. Если пришел очередной ожидаемый пакет, т.е. если хранимая в 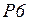фишка 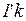имеет тот же номер, что и фишка 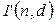( 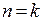), то после задержки 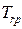происходят следующие действия:

- принятый пакет 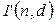передается получателю в 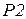с временной меткой ;

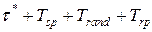- содержимое счетчика в 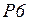увеличивается на 1;

- в 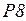отправляется фишка 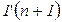с временной меткой .

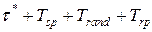Если же в 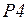пришло «пустое» сообщение (т.е. 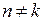), то в 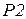ничего не передается, содержимое 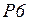не изменяется и в позицию 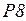отправляется фишка с прежним номером 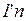и указанной выше временной меткой.

Передача «квитанции» по обратному каналу происходит аналогичным образом. Фишка 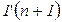или 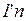с накопленной временной задержкой проходит через переход 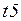, при этом временная метка увеличивается на случайную величину 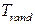. Затем на дуге 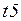to 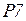происходит проверка потери «квитанции». При срабатывании датчика 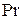в позицию 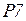вместо фишек 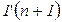или 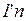приходит фишка 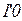. Переход 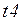анализирует пришедшую фишку. При совпадении номера пришедшей фишки с номером отправленной переход 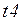срабатывает и отправляет фишку 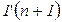в 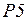, в противном случае срабатывания не происходит, и в 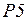остается прежний номер пакета 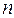. В первом случае может сработать переход 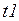и начнется передача пакета 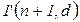в описанном выше порядке. Во втором случае система оказывается заблокированной до тех пор, пока предыдущий пакет по дуге 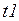to 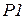не вернется в 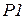. После этого начнется повторная передача пакета 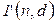с начальной временной отметкой .

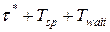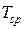
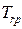
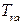
Описанная модель протокола передачи данных позволяет исследовать характеристики его работы. Варьируя времена задержки 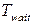, функции распределения величины 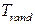и датчика 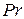, можно путем имитационного моделирования (многократного «прогона» пакетов через CPN) подобрать параметры протокола, обеспечивающие его эффективную работу.

4.3.4. Об исследовании сетей Петри с помощью ЭВМ

1. Специализированные программные средства. К настоящему времени разработано большое количество программных систем автоматизированного анализа сетей Петри, реализующих различные аспекты их использования: анализ общих сетей Петри и имитация их функционирования, ориентация на различные расширения этих сетей, использование средств машинной графики для ввода и редактирования сетей и др. Методы анализа общих и частных свойств сетей Петри - безопасность, ограниченность, консервативность, живость переходов, достижимость, наличие тупиков и циклов - также успешно реализуются на ЭВМ. Некоторые из этих программных систем являются автономными системами анализа сетей Петри (как, например, самая развитая и полная интерактивная система OVIDE [11]), в других сеть Петри используется в качестве имитационной модели, позволяющей провести верификацию и определить динамические характеристики реального моделируемого объекта (коммуникационных протоколов, систем с управлением потоком данных, логических схем, параллельных систем и др.).

Как уже упоминалось в п. 4.2, для анализа систем с помощью CPN создан специальный язык моделирования CPNML и соответствующий пакет программ [43].

Промышленные программы, предназначенные для анализа реальных вычислительных систем с помощью сетей Петри, обычно имеют дело с десятками и сотнями тысяч позиций и переходов и требуют соответствующих вычислительных ресурсов. Так, для моделирования процессора большой ЭВМ CDC 6600 потребовалась сеть Петри, содержащая около 500 тысяч позиций и переходов.

В рамках данного ознакомительного курса, естественно, нет необходимости обращаться к таким сложным и дорогостоящим системам. В то же время программирование работы небольших по объему сетей Петри и их расширений не представляет сложности для студентов третьего и четвертого курсов, обучающихся по направлениям, связанным с информационными технологиями. Поэтому составление таких программ предусмотрено в лабораторном практикуме и в качестве упражнений для самостоятельной работы.

2. Использование параллельных и кластерных вычислительных систем. Как мы видели выше, исследование сетей Петри реальных размерностей представляет собой сложную задачу компьютерного моделирования. Поэтому понятен большой интерес к оценке возможностей, которые открываются при использовании для этих целей кластерных вычислительных систем, и алгоритмов параллельных вычислений. Этот интерес оправдывается еще и тем, что кластерные вычислительные системы становятся доступными не только ведущим научным учреждениям, но широкому кругу исследователей, в том числе студентам.

Ниже рассмотрен один из возможных подходов к распараллеливанию процесса построения дерева маркировки обыкновенной сети Петри [11].

В отличие от задач, в которых имеется весь исходный материал для вычислений и трудоемкость которых зависит от размерности и трудоемких математических операций, в данном случае основные временные затраты приходятся на порождение дерева маркировок, которое растет динамически. Предсказать скорость роста и размеры дерева либо провести качественный анализ можно лишь в отдельных случаях.

проблему можно попытаться решить, если распараллеливать вычисления по мере роста дерева, т.е. обрабатывать каждую новую ветку на отдельном потоке. Таким образом, получится, что каждый узел кластера будет обрабатывать свое собственное поддерево.

Для определения некоторых параметров, например поиска циклов, необходимо иметь все дерево маркировок. Поиск циклов необходимо производить после получения новой маркировки. Поэтому нужно либо передавать все дерево на каждый узел кластера (при этом растет нагрузка на сеть, т.к. нужно часто передавать большие объемы данных), либо хранить все дерево маркировок на одном узле. При этом повышаются требования к производительности этого узла, но, с другой стороны, массированные операции парного сравнения разметок могут быть также выполнены в параллельном режиме. В этом же процессе может производиться порождение свободного словаря сети Петри.

Если ставить перед собой только задачу прямой достижимости (или другие задачи, не требующие операций над всем деревом маркировок одновременно), то тогда проблема хранения этого дерева вообще не возникает. В противном случае эту проблему можно разрешить, также распределив и эти вычисления. Например, поиск циклов выполнять не сразу по всему дереву, а только в том поддереве, которое доступно в данный момент, а дальнейшем производить вторичный поиск в оставшихся ветках. Программирование и решение этой задачи может составить содержание курсового проекта или выпускной квалификационной работы.

4.4 ГЕРТ-сети

4.4.1 Описание ГЕРТ-сети

Структура ГЕРТ-сети может быть описана в виде графа

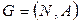, (4.23)

где 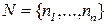–множество узлов сети, 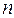- количество узлов,

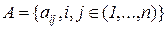– множество ориентированных дуг. Дуга 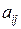соединяет два узла 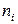и 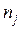и направлена от 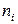к .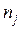

Среди узлов выделяют источники (начальные вершины графа) истоки (конечные вершины графа).

Узлы ГЕРТ-сети интерпретируются как состояния системы, а дуги – как переходы из одного состояния в другое. Такие переходы связываются с выполнением обобщенных операций, характеризуемых плотностью распределения случайных величин и вероятностью выполнения операции.

Каждый узел 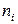может находиться в пассивном и активном состоянии. В последнем случае говорят, что узел выполнен.

Дуга 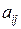в ГЕРТ-сети также может находиться в пассивном и активном состоянии (выполняться), кроме того, она характеризуется некоторым аддитивным параметром (называемым «весом дуги» или «работой на дуге»). В качестве этого параметра выступает вектор [ 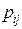, 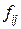], где 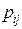– условная вероятность выполнения дуги 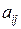при условии активации узл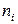а , а 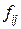– условная функция распределения времени выполнения дуги 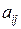при условии, что работа на этой дугевыполняется. Вместо функций 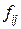могут использоваться их преобразования – производящие функции M_ij , которые будут рассмотрены ниже. На дуге 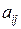, для которой 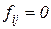, работа не выполняется, она называется «холостой» дугой.

Каждый узел сети имеет входную и выходную функции активации. Входная функция определяет условие, при котором узел может быть активирован. Выходная функция определяет совокупность условий, порождаемых в результате активизации узла.

Активация узла означает, что система перешла в некоторое новое состояние, и определяет множество дальнейших работ (операций). Эти работы (операции) начинают свое выполнение сразу после активации узла, являющегося их началом. Активация узла происходит, если его функция на его входной дуге выполнена. После выполнения выходной функции активированного узла он становится неактивным.