Задания для самостоятельной работы 4 страница

Пример. Приведем описание простой CPN, схема которой и начальная маркировка приведены на рисунке 4.7 а.

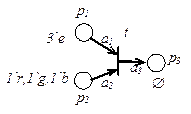
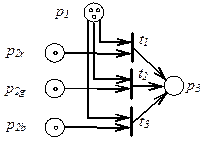
а) б)

Рис. 4.7. Раскрашенная сеть Петри и эквивалентная ей обыкновенная СП

· Множества цветов:

; .

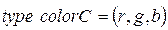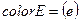· Переменные:

; .

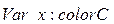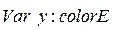· Множество позиций:

.

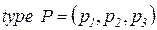· Множество переходов:

.

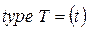· Множество дуг , , , , ,

; ;

; ;

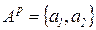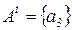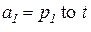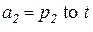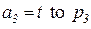
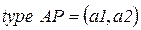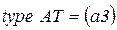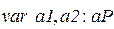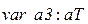· Цветовая функция

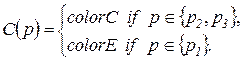
· Блокировочная функция отсутствует: .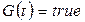

· функция 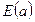, задающая выражения на дугах:

;

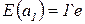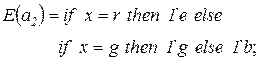
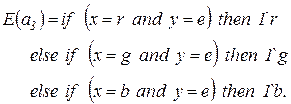
· функция инициализации 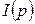, задающая начальную маркировку ; ; .

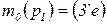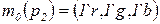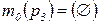Ниже приведено полное дерево маркировок рассмотренной сети.

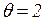
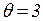
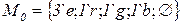
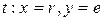
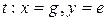
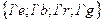
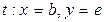
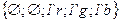
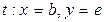
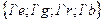
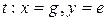
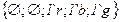
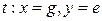
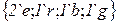
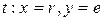
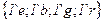
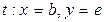
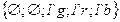
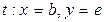
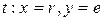
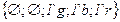
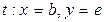
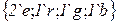
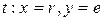
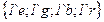
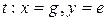
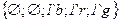
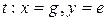
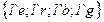
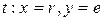
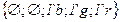
Поясним описание сети. Для позиции 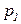разрешен цвет 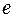, для позиций 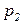, 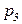разрешены цвета 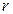, , 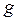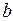. Переход 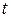может сработать, если в позиции 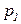находится хотя бы одна фишка цвета 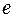и в позиции 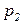находится хотя бы одна фишка цветов , , .

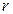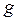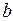В позицию 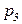при срабатывании перехода пересылается та фишка, которая была извлечена из 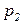при срабатывании перехода. Начальная маркировка – 3 фишки цвета 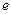в позиции 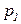, по одной фишке всех цветов в позиции .

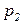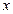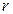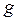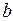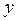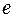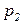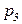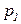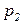При работе сети переменная принимает поочередно (в произвольном порядке) значения , , , а переменная - значение . Работа сети продолжается до тех пор, пока все фишки из не будут пересланы в . При этом позиции и оказываются пустыми. Дерево маркировок описывает все возможные варианты последовательности пересылки фишек.

Эквивалентная рассмотренной CPN обыкновенная сеть Петри приведена на рисунке 4.8 б.

Построив дерево маркировок этой сети, нетрудно убедиться, что оно структурно совпадает с рассмотренным выше деревом CPN. Однако раскрашенная сеть содержит больше информации, поскольку ресурсы в позиции 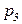не обезличиваются, и можно проследить порядок их поступления.

4.2.4 Расширения CPN

Как уже отмечалось в п. 4.1.5, использование сетей Петри в различных прикладных задачах может потребовать придания им дополнительных возможностей, что приводит к созданию расширений этих сетей. Некоторые расширения аналогичны рассмотренным в п. 4.1.5, (например иерархические CPN), потребность в ряде других отсутствует, т.к. формализм CPN позволяет их описать (CPN с приоритетами, ингибиторные сети, самомодифицируемые сети).

Ниже мы рассмотрим одно важное расширение CPN, значительно увеличивающее их моделирующие возможности: CPN с временным механизмом.

Существует ряд задач моделирования, в которых необходимо учитывать не только последовательность событий, но и время их наступления, а также продолжительность. Для этой цели предусмотрено расширение возможностей раскрашенных сетей Петри путем введения временного механизма (так называемых timed CPN [42]). В несколько упрощенном виде сущность такого расширения описана ниже.

А. В модель системы вводятся часы, показывающие глобальное время . Обычно это время считается дискретным, т.е. означает номер такта, выдаваемого тактовым генератором системы моделирования. Глобальное время 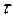отличается от времени 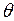, которое содержится в определении (4.13), поскольку 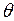есть номер шага работы CPN, а 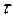изменяется независимо от работы сети.

Б. Ресурсы, перемещаемые в сети (фишки) могут получить временные метки. Такие ресурсы, в общем виде, задаются мультимножествами с временными метками (timed multi-sets), однако мы эту теорию не рассматриваем. Отметим лишь, что при описании множества цветов добавляются пометки timed, а переменные соответствующего типа снабжаются знаками @ (по-английски читается at, т.е. «во время»). Это означает, что переменная привязана к глобальному времени. После значка @ в квадратных скобках указывается значение глобального времени, в течение которого возможно использование данных фишек при срабатывании переходов, для которых они являются входными. При этом запись вида @[500] говорит о том, что фишка «включается» в момент 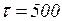и далее готова для работы в сети, а запись @[500, 600] означает, что фишка может использоваться в диапазоне глобального времени .

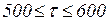Приведем пример.

;

;

;

.

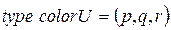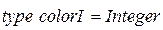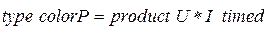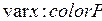Возможное значение мультимножества определяемого переменной :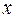

.

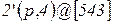В. Каждый переход, на вход которого поступают фишки, имеющие временные метки, получает дополнительное условие срабатывания: он может сработать только в том случае, если системное время удовлетворяет всем условиям на входных фишках.

В свою очередь, при срабатывании переход может увеличить временную метку фишки, т.е. смоделировать задержку в работе системы. Величина задержки определяется специальным выражением связанным с переходом, и имеющим вид 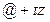, где 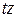- время задержки, задаваемое числом или функцией.

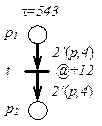
Рис. 4.8. Фрагмент CPN с временными метками

Пусть в сети на рисунке 4.8 начальная маркировка такова:

, .

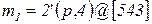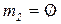Выражения на дугах показаны на схеме. Глобальное время 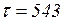. Переход 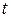может сработать, при этом он осуществит задержку передачи фишек в 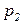на 12 единиц времени в соответствии с выражением на 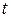. Таким образом, после срабатывания 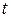получим маркировку:

, .

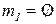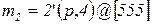Пример CPN с временным механизмом приведен в п. 4.3.3.

4.2.5 Сравнение формализмов обыкновенных и
раскрашенных сетей Петри

Подведем некоторые итоги данного раздела. Мы кратко рассмотрели теорию сетей Петри в двух вариантах:

· формализм классических или обыкновенных СП (РТ – сетей в терминологии К. Йенсена);

· формализм раскрашенных сетей Петри - CPN.

Нетрудно убедиться в том, что формализм описания структуры и функционирования CPN справедлив и для обыкновенных СП. При этом пункты 1, 3, 4 и 10 совпадают с описанием в разделе 4.1.1; цветовое множество всего одно и имеет единственный цвет; описание связей между узлами вместо матриц 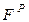и 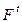следует задавать множеством дуг 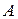, узловой функций 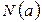и выражениями на дугах 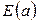. Функция 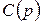тривиальна и поэтому не нужна, а функция всегда истинна. Правила срабатывания и изменения маркировок (4.20) и (4.21) при сделанных предположениях совпадают соответственно с (4.6) и (4.7). В то же время очевидно, что формализм CPN К. Йенсена при всех своих преимуществах в ряде случаев более громоздок и менее удобен по сравнению с формализмом классических обыкновенных сетей Петри. Поэтому при моделировании конкретных систем исследователь должен выбирать наиболее подходящую в данном случае методологию. Именно так мы и будем поступать в дальнейшем.

4.2.6 О моделирующих возможностях сетей Петри

С точки зрения инженерных приложений наибольший интерес представляет анализ динамики изменения маркировок сети Петри и возникающих при этом ситуаций.

Однако важен и вопрос о том, насколько широкий класс объектов могут моделировать сети Петри. В п. 4.1.3 говорилось о свободном языке сети Петри, который представляет собой некоторое подмножество всех слов в алфавите T. Множество свободных языков всех сетей Петри образует класс свободных языков сетей Петри.

В ряде случаев язык сети Петри можно изменить, связав с некоторыми переходами сети N определенные символы из алфавита 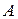, и часть переходов оставить непомеченными (вернее, помеченными пустым символом l). В этом случае говорят о помеченной сети Петри 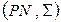, где 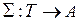– помечающая функция, ставящая в соответствие переходам 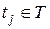символы 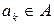. Ясно, что обычная сеть Петри есть частный случай помеченной сети Петри при .

Помеченную сеть Петри можно рассматривать как генератор слов и изучать ее возможности с точки зрения математической лингвистики.

Рассмотренные в п. 4.1.5 расширения сетей Петри порождают другие классы языков.

Эти классы языков интересно сравнивать с языками, порождаемыми иными типами абстрактных систем, в частности с языками конечных автоматов и машин Тьюринга. Такое сравнение позволяет характеризовать моделирующие возможности сетей Петри, их способность адекватно описывать системы со сложной динамикой функционирования.

В монографии В.Е. Котова [18] доказываются следующие утверждения:

1. Класс помеченных сетей Петри строго мощнее класса конечных автоматов и строго менее мощен, чем класс машин Тьюринга.

2. Классы ингибиторных сетей и сетей с приоритетами строго мощнее класса сетей Петри и равномощны классу машин Тьюринга.

3. Класс раскрашенных сетей при конечном количестве цветов равномощен классу сетей Петри.

4. Класс самомодифицируемых сетей эквивалентен классу ингибиторных сетей и сетей с приоритетами.

4.3 Моделирование дискретных систем

Сети Петри были разработаны и используются для поддержки принятия решений путем моделирования и исследования сложных систем. С помощью различных модификаций этих сетей можно описать многие системы, в особенности системы с независимыми элементами, например, аппаратное и программное обеспечение ЭВМ, системы телекоммуникаций, физические, химические, экономические, социальные и другие системы.

При описании сетей Петри выделяют два понятия: события и условия.

Событие– это действие в системе. В сетях Петри они моделируются переходами.

Условие – предикат или логическое описание системы, принимающее значение «истина» или «ложь». Условия моделируются позициями и условиями на дугах. Различаются предусловия и постусловия.

Предусловие – это условие до срабатывания перехода, постусловие – соответственно условие после срабатывания перехода.

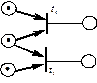
рис. 4.9. Сеть Петри, моделирующая конфликт

Если процесс в системе достаточно сложный, то его подсистемы можно представить в виде непримитивных событий. На рисунке. 5, составной переход – непримитивное событие, моделируемое отдельной сетью Петри. При этом процесс моделируется иерархической сетью Петри (п. 4.1.5).

Следующая особенность Сети Петри - одновременность. Если переходы и 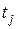не влияют друг на друга, то в возможный словарь языка сети Петри входят как слова, начинающиеся с 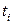, так и слова начинающиеся с t_j.

Еще одна ситуация называется конфликтом.

Переходы 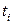и 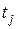находятся в конфликте, если запуск одного из них блокирует запуск другого (рисунок 4.9).

Рассмотрим несколько примеров применения сетей Петри.

4.3.1 Моделирование вычислительных систем

1. Простейшая система массового обслуживания. Рассмотрим систему массового обслуживания (СМО), например, вычислительную систему, схема, которой показана на рисунке 4.10 а. Система имеет входной и выходной потоки заданий, и пока она занята выполнением очередного задания, она не может ввести следующее задание.

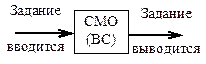
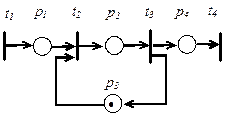
а) б)

рисунок 4.10. Общее представление о системе массового обслуживания (а) модель простейшей СМО в виде сети Петри (б)

Модель СМО в виде сети Петри показана на рисунке 4.10б.

Рассмотрим множество условий и событий, характеризующих систему.

условия:

p₁ - задание ждет обработки,

p₂ - задание обрабатывается,

p₃ - процессор свободен,

p₄ - задание ожидает вывода.

события:

t₁ - задание помещается во входную очередь,

t₂ - начало выполнения задания,

t₃ - конец выполнения задания,

t₄ - задание выводится.

Поясним работу данной сети. Показанная на рисунке начальная маркировка 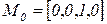соответствует состоянию, когда система свободна, и заявки на обслуживание отсутствуют. При срабатывании перехода (от внешнего источника) поступает задание и получается маркировка 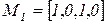. При этом может сработать переход 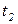, что означает начало обслуживания задания и приводит к маркировке 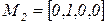. Затем может сработать переход 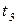, что означает окончание обслуживания задания и освобождение системы, т.е. переход к маркировке 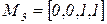. 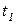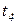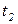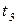Переходы и могут работать независимо от и моделируя поступление и вывод заданий. Построение сети Петри, моделирующей последовательность обслуживающих устройств, соединенных в очередь типа FIFO, предлагается в качестве задания для самостоятельной работы.

2. Двухпоточная СМО. Пусть теперьСМО выполняет задания, поступающие от двух источников и находящиеся в двух очередях. Вывод обработанных заданий осуществляется одним потоком. В этом случае модель системы имеет вид, показанный на рисунке 4.11.

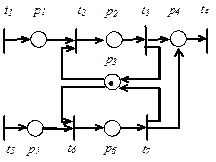
рисунок 4.11. Модель СМО с двумя потоками входных заявок

Здесь введены дополнительные условия:

p₅ – задание из второй очереди ждет обработки;

p₆ – задание из второй очереди обрабатывается,

и дополнительные события:

t₅ – задание помещается во вторую очередь;

t₆ – начало выполнения задания из второй очереди;

t₇ – завершение выполнения задания из второй очереди.

Как видно, здесь имеет место конфликт. Одновременно может выполняться только одно задание из любой очереди.

В то же время, если в позиции p₃ имеются две заявки (это соответствует двухпроцессорной системе), то возможно одновременное выполнение двух заданий из обеих очередей в любой комбинации.

3. Конвейер. В качестве следующего примера рассмотрим схему управления асинхронной ЭВМ с конвейерной обработкой.

Поясним работу конвейера на примере операции сложения двух двоичных чисел с плавающей точкой

,

.

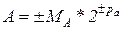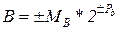Здесь

М_А , М_В – мантиссы чисел А и В,

р_а, р_b – двоичные порядки этих чисел.

Требуется получить результат

.

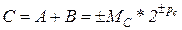Как известно, эта операция состоит из следующих этапов:

СП – сравнение порядков;

ВП – выравнивание порядков;

СМ – сложение мантисс;

НР – нормализация результата.

Каждый из этих этапов выполняется отдельным функциональным устройством в устройстве конвейерной обработки. Связь между функциональными устройствами и синхронизация их работы осуществляется с помощью пары регистров: входного Pг_i и выходного Pг_o

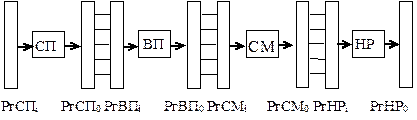
рис. 4.12. Схема конвейера при сложении двух чисел

Выпишем для i-того функционального устройства условия:

p_i1 – входной регистр свободен;

p_i2 – входной регистр заполнен;

p_i3 – блок занят;

p_i4 – выходной регистр свободен;

p_i5 – выходной регистр заполнен;

p_i6 – пересылка в следующий блок возможна;

и события:

t_i1 – начало работы i-го блока;

t_i2 – завершение работы i-го блока;

t_i3 – начало пересылки в (i+1)-й блок;

t_i4 – завершение пересылки в (i+1)-й блок.

При этом модель i-го блока конвейера при начальной маркировке примет вид, показанный на рисунке 4.13.

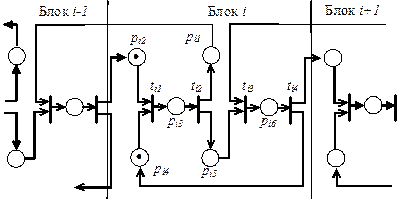
рис. 4.13 Сеть Петри, моделирующая фрагмент конвейера

Предоставляем читателям самостоятельно проследить последовательность срабатывания переходов и получаемые при этом маркировки.

4. Вычислительная система с альтернативными ресурсами. Рассмотрим пример моделирования, в котором удобно использовать раскрашенные сети Петри.

Пусть необходимо смоделировать фрагмент вычислительной системы, в которой осуществляются обмены между тремя накопителями на магнитных дисках D₁, D₂, D₃ и центральным процессором ЦП через два канала С₁ и С₂. При этом требуется, чтобы D₁ использовал канал С₁, D₂ - канал С₂, D₃ - оба канала С₁ и С₂ (рисунок 4.14).