Задания для самостоятельной работы 3 страница

Вектор 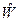, удовлетворяющий условию (4.12), называется инвариантом переходов.

Приведенные рассуждения легко обобщаются и на случай, когда число линейно зависимых строк (и столбцов) в матрице 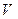больше двух. Напомним, что число линейно независимых строк матрицы 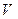равно числу ее линейно независимых столбцов и равно рангу матрицы 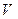, который обозначается буквой 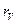. Величина 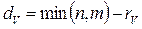называется дефектом матрицы 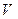. Таким образом, для того, чтобы можно было построить инварианты позиций и переходов сети Петри 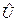, 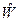удовлетворяющие условиям (4.10, 4.12), необходимо, чтобы дефект матрицы 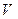был больше нуля: .

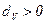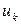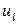Из сказанного вытекает также, что задача нахождения инвариантов сети Петри решается неоднозначно. Так, например, умножив веса и на постоянное число 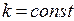, мы получим другой вектор-инвариант 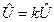, который обладает теми же свойствами, что и .

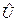Отметим один частный случай. Если для некоторой сети Петри существует вектор-инвариант позиций 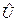, все элементы которого равны единице, то это означает, что при работе сети сумма фишек во всех позициях постоянна и равна этой сумме в начальной маркировке:

, .

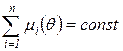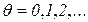Такая сеть Петри, как было сказано выше, называется консервативной.

Пример. Рассмотрим сеть Петри, изображенную на рисунке 4.1, и составим для нее матрицу :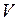

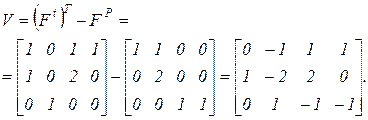
Легко видеть, что в этой матрице первая и третья строки линейно зависимы, причем достаточно взять веса 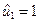, , 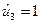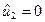. При этом получим вектор-инвариант по позициям 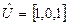, следовательно, сумма фишек в позициях 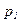и 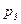постоянна при срабатывании любого перехода: 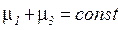, в чем легко убедиться, проанализировав дерево маркировок на рисунке 4.2.

Рассмотрим теперь столбцы матрицы 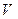. Мы видим, что второй и третий столбец линейно зависимы, при этом вектор-инвариант по переходам может быть взят следующим:

.

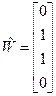Это означает, что при последовательном срабатывании переходов 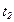, 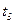(в любом порядке) маркировка сети повторяется. Это также видно на рисунке 4.2.

4.2 Раскрашенные (цветные) сети Петри (CPN)

В последние годы широко используется методология моделирования дискретных систем, основанная на использовании раскрашенных (цветных) сетей Петри – Coloured Petri Nets (CPN). Эта методология является обобщением формализма обыкновенных сетей Петри на случай многих видов ресурсов и позволяет более эффективно моделировать сложные системы. На базе методологии CPN разработан специальный язык моделирования – Coloured Petri Nets Modeling Language (CPN ML) и созданы соответствующие программные средства.

Правила функционирования CPN сложнее правил для обыкновенных сетей Петри. В то же время структура сети – двудольный ориентированный мультиграф и основной шаг работы – изменение маркировок при срабатывании переходов – принципиально не различаются.

Ниже рассмотрено несколько упрощенное и по возможности неформа-лизованное описание CPN, ориентированное на синтаксис языка Паскаль. Полное и строгое описание CPN содержится в книге Курта Йенсена [42].

4.2.1 Мультимножества

Одним из важных понятий, используемых в теории раскрашенных сетей Петри, является понятие мультимножества.

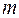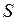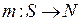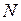Формально мультимножеством на непустом множестве называется функция , где - множество натуральных чисел.

Иными словами, мультимножество 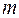состоит из элементов множества 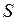, каждый из которых может быть повторен 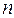раз ( 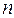- переменная целого типа). мультимножество может быть представлено в виде кортежа, в котором перечислены входящие в него элементы с указанием их кратности. Указатель кратности – выражение целого типа - ставится перед названием элемента множества и отделяется от него кавычкой. Отсутствие какого либо элемента из 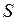в мультимножестве эквивалентно его присутствию с нулевой кратностью. Формально мультимножество на 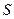можно представить суммой

,

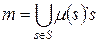где 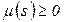– число появлений (кратность) элемента 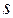в мультимножестве .

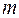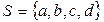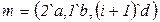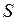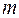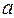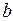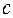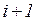Пример. Пусть – множество элементов и – мультимножество на . Последняя запись означает, что состоит из двух элементов , одного элемента , нуля (ни одного) элементов и элементов 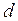, где 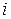– переменная типа integer.

Рассмотрим операции над мультимножествами.

1. Сложение мультимножеств.

Пусть , .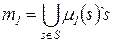

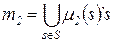Тогда .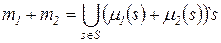

2. Умножение мультимножества на скаляр.

Пусть 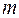мультимножество, 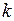- скаляр типа integer.

Тогда .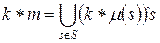

3. Сравнение мультимножеств.

Мы будем говорить, что ,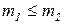

если .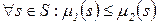

4. Вычитание мультимножеств. если 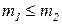, то можно определить разность мультимножеств:

.

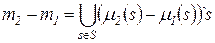5. Мощность мультимножества – суммарное число элементов в мультимножестве:

.

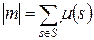4.2.2 Формальное определение CPN

раскрашенная сеть Петри CPN – это кортеж

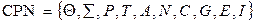. (4.13)

Рассмотрим элементы определения (4.13).

1. 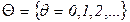- множество дискретных моментов времени (шагов), в которые происходит функционирование сети. Номер шага есть переменная целого типа:

var teta: Integer; .

2. 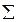– конечное множество непустых типов, называемое цветами. Типы имеют общее название 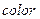и задаются аналогично тому, как это принято в языках программирования. Например:

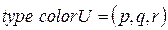; – перечисляемый тип, здесь 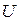- имя цветного множества, 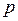, , 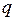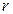– входящие в него цвета;

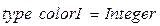; – целый тип;

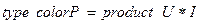; – прямое произведение типов.

При описании переменных, используемых в сети, указывают их принадлежность к типу, например:

; ; .

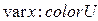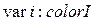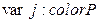В последнем примере переменная 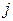состоит из пары элементов 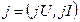, где элемент 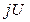принадлежит типу 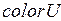, а 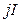– типу .

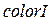3. – конечное множество позиций. Это множество может быть представлено перечисляемым типом:

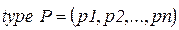; (4.14)

а для работы с ним вводится переменная

.

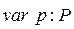С каждой позицией может быть связана определенная маркировка, которая учитывает наличие различных типов ресурсов. Маркировка позиции 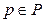представляет собой мультимножество, например, следующего вида:

.

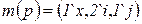Здесь 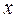, , 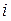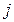- переменные указанных в п.2 цветовых типов, определяющие различные виды ресурсов, а цифры, стоящие перед кавычками, – количество фишек соответствующего типа, в позиции .

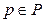Совокупность маркировок всех позиций называется маркировкой сети:

.

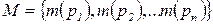В языке Паскаль мультимножество, определяющее маркировку позиции, может быть представлено, например, типом – множество, состоящим из записей вида

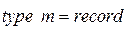; (4.15)

; ; ; .

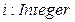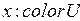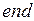Операции над мультимножествами можно определить соответствующими процедурами. Аналогично определяется мультимножество, задающее маркировку сети.

4. – конечное множество переходов, которое можно представить перечисляемым типом

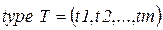; (4.16)

и соответствующей переменной:

.

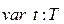Это множество не отличается от множества переходов для обыкновенных сетей Петри, однако правила их срабатывания могут быть более сложными. Эти правила рассмотрены ниже.

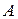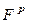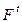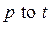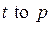5. – конечное множество дуг, связывающих между собой позиции и переходы. В отличие от обыкновенных сетей Петри, где дуги задаются матрицами инцидентности и , в языке CPN ML указываются все дуги с помощью выражений вида: и , где 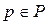, 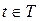. Такая нотация введена для того, чтобы можно было пару элементов 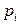, 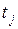соединить несколькими дугами с различными свойствами.

В этих выражениях первый элемент указывает начало дуги, второй элемент – конец дуги.

множество 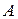имеет следующую структуру:

,

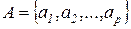где дуги 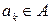определяются одним из видов выражений:

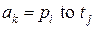или , , .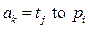

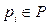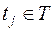Поскольку дуги имеют два вида: от позиции к переходу ( 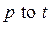) и от перехода к позиции ( 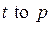), то множество 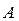можно представить в виде суммы непересекающихся множеств:

, ,

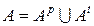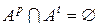где множество 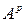содержит элементы вида 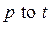, а множество 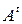–элементы вида .

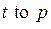Как и в случае обыкновенных сетей Петри, элементы множеств , , 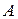не пересекаются:

.

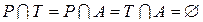6. 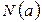– узловая функция, которая для каждой дуги 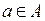указывает ее исходный и конечный узел. Формально

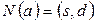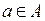, , если в множестве 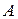элементу 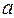соответствует выражение 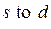. Здесь 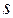- имя узла, от которого начинается дуга, 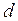– имя узла, где она заканчивается.

Рассмотрим один из способов задания этой функции.

Каждая дуга может быть представлена в виде записи. Дуги типа 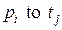задаются записью

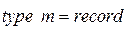; (4.17)

; ; ; .

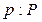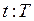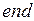Дуги типа 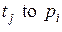задаются аналогично:

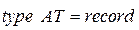; (4.18)

; ; ; .

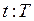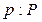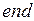Множества дуг 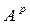и 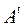могут быть представлены перечисляемыми типами:

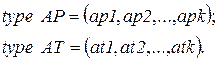(4.19)

Для работы с дугами вводятся переменные соответствующих типов:

; .

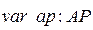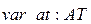7. 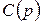– цветовая функция, определяющая множество типов цветов, разрешенных для каждой позиции. Например, запись

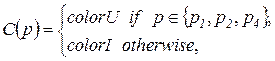
означает, что цвета типа 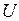разрешены для позиций 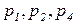, а цвета типа 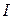разрешены для всех остальных позиций из .

8. 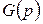– блокировочная (спусковая) функция, описывающая дополнительные условия, которые должны быть выполнены для срабатывания перехода 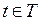. Эта функция представляет собой предикат, составленный из переменных, принадлежащих типам цветов 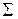. Например, функция

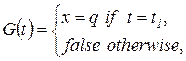
принимает истинное значение для перехода 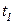, если переменная 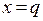, а во всех остальных случаях она ложь. Таким образом, для того, чтобы было разрешено срабатывание перехода 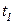, требуется выполнение дополнительного условия 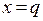на входной дуге к 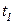. Если эта функция не определена, то по умолчанию предполагается истинной.

9. 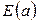– функция, задающая выражения на дугах 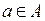. Эта функция для каждой дуги 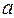определяет мультимножество, состоящее из элементов, описанных в множестве цветов 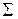. Мы будем говорить, что это мультимножество помечает дугу. Введение в CPN функции 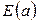является развитием понятия кратности дуг в формализме обыкновенных СП.

Рассмотрим примеры задания функции .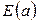

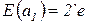
- дуга 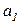помечается двумя фишками типа ;

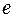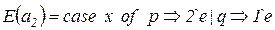
- дуга 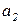помечается двумя фишками типа 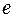, если переменная 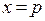, и одной фишкой типа 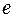, если .

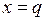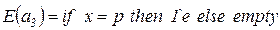
- дуга 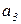помечается одной фишкой типа 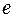, если 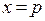, иначе не помечается.

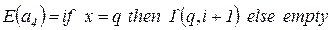
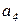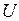- дуга помечается одной фишкой типа состоящей из типов и 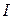(см. пример в п. 2 определения), если 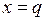, и не помечается в противном случае.

Отсутствие выражения для какой-либо дуги означает, что дуга не помечена.

9. 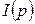- функция инициализации сети CPN. Эта функция по аналогии с обыкновенными СП задает начальную маркировку (разметку) сети 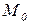, т.е. для каждой позиции 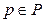указывает цветовое мультимножество, обозначаемое .

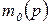Например, 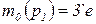; ; 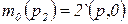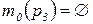- начальные маркировки позиций; 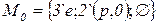- начальная маркировка сети.

4.2.3 Функционирование CPN

Рассмотрим работу раскрашенных сетей Петри. Как и в случае обыкновенных СП, функционирование сети состоит в срабатывании переходов и происходящих вследствие этого изменениях маркировок.

Мы будем говорить, что переход 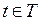может сработать (может быть запущен), если выполняется условие:

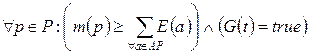. (4.20)

В первой скобке выражения (4.20) происходит поэлементное сравнение мультимножества, являющегося маркировкой позиции 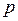с мультимножеством, которым помечены дуги, ведущие от 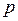к.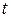

Суммирование мультимножеств 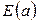связано с тем, что, как отмечалось в п.5, два узла могут быть соединены несколькими дугами, и суммирование производится по всем таким дугам.

Во второй скобке записано условие отсутствия блокировки перехода 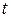(см. п. 8 определения).

Если условие срабатывания перехода 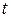выполняется, то он может сработать, при этом говорят, что выполнится шаг работы CPN. Отсчет шагов производится в дискретном времени 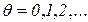. Поэтому маркировку отдельных позиций 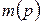и сети в целом 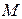мы будем также привязывать ко времени и записывать соответственно в виде 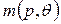и .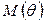

Изменение маркировки узла 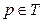при осуществлении шага работы CPN рассчитывается по формуле:

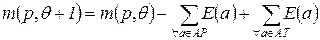. (4.21)

В выражении (4.21) все слагаемые являются мультимножествами, и вычисления производятся в соответствии с правилами сложения и вычитания мультимножеств. Знаки суммирования мультимножеств используются в формуле по причине, которая уже пояснена выше: каждая пара узлов может быть связана несколькими дугами, а каждая дуга 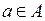помечена отдельным выражением 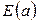. Если на некотором шаге 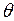выполняются условия срабатывания нескольких переходов, то по аналогии с обыкновенными СП, в зависимости от задачи исследования CPN мы можем разрешить сработать всем переходам (при построении дерева возможных маркировок) либо дать такую возможность только одному из них на основе некоторых дополнительных условий (например, приоритетов).