Методика экономического анализа.
В отличие от метода экономического анализа как общего подхода к исследованию явлений выделяют методику экономического анализа как совокупность специальных приемов (методов), применяемых для обработки экономической информации. методику экономического анализа подразделяют на общую и частную. Общая методика представляет собой совокупность приемов аналитической работы в любой отрасли народного хозяйства, в любом виде хозяйственной деятельности. Частная методика конкретизирует общую методику применительно к хозяйственным процессам, происходящим в определенной отрасли народного хозяйства, к определенному типу производства. Степень конкретизации частных методик может быть различной.
Традиционные методы экономического анализа. Важнейшими способами обработки экономической информации, применяемыми при анализе экономики, являются сводка и группировка, абсолютные и относительные величины, средние величины, ряды динамики, индексы, метод цепных подстановок, элиминирование и др.
Сводка и группировка – важные элементы экономического анализа. Путем сводки можно подвести общий результат действия различных факторов на выпуск продукции, снижение себестоимости, повышение рентабельности и т.д.
Группировкой называют выделение среди изучаемых явлений характерных групп и подгрупп по тем или иным признакам. Сгруппированные данные обычно оформляются в виде таблиц. Такая таблица представляет собой форму рационального изложения цифровых характеристик, изучаемых явлений и процессов. Данные в таблице располагаются так, чтобы легко было сделать вывод из анализа.
Абсолютные и относительные величины. С помощью абсолютных величин характеризуются размеры (уровни, объемы) экономических явлений и показателей. Относительные величины используются для характеристики степени выполнения планов, измерения темпов (относительной скорости) развития производства и т.д. Величина, полученная в результате сопоставления двух однородных показателей, один из которых принимается за единицу, называется коэффициентом. Особой формой относительных величин являются проценты, при которых базисная величина принимается не за 1, а за 100. Относительные величины иногда выражаются в промилле, когда базисная величина принимается за 1000. В каждом отдельном случае надо выбрать такую форму относительной величины, которая выразила бы интересующее нас соотношение с наибольшей наглядностью.
Средние величины. Для обобщающей характеристики массовых, качественно однородных экономических явлений пользуются средними величинами, способы расчета которых различны.
Средняя величина выражает относительную особенность данной совокупности явлений, устанавливает ее наиболее типичные черты. Степень колеблемости признака необходимо изучать, чтобы получить более полное представление об изучаемом объекте.
Некоторое представление о степени колеблемости дает вариационный ряд, в котором отражаются все уровни с указанием, насколько часто встречается каждый уровень. Простейшей мерой колеблемости является размах вариации – расстояние между наибольшим и наименьшим вариантом. Для более точного отражения степени колеблемости используют также среднее линейное отклонение, среднее квадратическое отклонение и коэффициент вариации.
Ряды динамики. Рядом динамики называется ряд данных, характеризующих изменение явления, показателей по времени. Каждое отдельное значение показателя ряда динамики называется уровнем. Для характеристики изменения уровня ряда динамики исчисляют абсолютный прирост и темп роста и прироста.
Темп роста характеризует степень изменения уровня продажи продукции от одного года к другому. Для получения общей характеристики темпа изменения уровня продукции за весь период исчисляют средний темп. Характеристикой среднего темпа служит средняя геометрическая из темпов. Для расчета среднего темпа роста и прироста динамического ряда применяется логарифмирование.
Индексы – относительные показатели сравнения таких явлений, которые состоят из элементов, непосредственно не поддающихся суммированию. Так, большинство предприятий изготавливают разнородную продукцию, которую невозможно суммировать – например, нельзя складывать число автобусов, грузовых автомобилей, велосипедов, выпускаемых автомобильным заводом; однако общим для них является то, что они есть продукты труда и имеют стоимость. Значит, количество автобусов, грузовиков и велосипедов можно складывать, используя трудовые измерители или рубли. Но как трудовые измерители, так и цены не постоянны. Если сравнить, например, продукцию предприятия за два года, то разница в показателе будет результатом изменения как количества продуктов, так и цен на эти продукты.
С помощью индексов можно рассчитать изменение отдельно количества продуктов и отдельно – цен на продукцию. Для определения изменения количества выпущенных изделий вся продукция отчетного и базисного года оценивается в одинаковых постоянных ценах (обычно в ценах базисного года). И наоборот, для определения изменения цен за эти годы продукция одного года (обычно отчетного) оценивается в ценах старых и новых.
С помощью индексов сравнивают данные не только двух периодов, но и данные за ряд лет. В этом случае используют индексы цепные и базисные. Примером цепных индексов может быть таблица о темпах роста продажи продукции, где изделия каждого года сравниваются в сопоставимых ценах с продукцией предшествующего года. При расчетах базисных индексов базу сравнения принимают за 100, а вес последующие показатели выражают в процентах (или коэффициентах) к базисной величине.
Метод цепных подстановок. Индексный метод широко применяется для анализа роли отдельных факторов. Обычно экономический показатель можно разложить на ряд составляющих его факторов или показателей. Например, объем продукции есть результат умножения таких факторов, как часовая выработка, продолжительность рабочего для, число дней, отработанных каждым рабочим, число рабочих. Если все факторы плановые, то в результате получим плановый объем продукции; если все факторы фактические – фактический объем продукции. Сущность приема цепных подстановок заключается в последовательной замене плановой (базисной) величины каждого фактора величиной фактической. После каждой замены новый результат сравнивают с прежним. Например, если все факторы в формуле плановые, а средняя часовая выработка фактическая, то полученный в итоге такой замены результат будет отличаться от планового объема продукции. Разница вновь полученного итога и планового объема есть результат влияния изменения часовой выработки.
Элиминирование. В экономическом анализе используются обобщающие показатели хозяйственной деятельности, на которые влияют как основные, так и побочные, внешние факторы. Метод, при помощи которого исключается действие ряда факторов и выделяется один из них, называется элиминированием. Оно осуществляется различными приемами, в том числе и способом цепных подстановок.
Детализация. Это последовательное расчленение изучаемых экономических явлений, показателей и факторов. Детализация позволяет на основе знания экономической теории упорядочить анализ, содействует комплексному рассмотрению всех факторов, влияющих на показатель, указывает значимость каждого фактора, является основой математического моделирования взаимной зависимости различных показателей и факторов. Детализацию можно проводить по различным признакам. Так, себестоимость продукции можно раскрыть по видам продукции (деталь, узел, изделие, сравнимая продукция, вся продукция), по факторам формирования затрат в сфере производства и сфере обращения (производство, снабжение, сбыт), по факторам формирования, например, в сфере производства (конструкция, техника и технология, организация производства и труда) и т.д. Особую ценность для экономического анализа представляет детализация показателей по их формированию и учету.
Балансовая увязка. В экономическом анализе используются различные балансовые сопоставления и увязки. Например, сопоставляется товарный баланс для определения суммы реализации товарной продукции и анализа влияния различных факторов на эту продукцию; сопоставляется баланс влияния различных факторов на итоговые показатели хозяйственной деятельности.
Особенностью бухгалтерского баланса является то, что он содержит сведения о капитале в двух разрезах: по размещению и назначению средств (актив баланса) и по источникам образования этих средств (пассив баланса). Например, производственные запасы в активе рассматриваются по видам; в пассиве же эти запасы исследуются по источникам формирования: собственные средства, кредиты банков и пр. рассматривать сопряженные статьи баланса можно в виде таблицы, где в подлежащем указываются запасы, а в сказуемом – источники их образования. Такое сопоставление даст ответ о правильности использования оборотных средств в форме производственных запасов или в других формах.
Отметим, что в экономическом анализе полезно использовать многие методы бухгалтерского учета и составления отчетности: метод двойной записи, калькуляции себестоимости отдельных изделий, нормативный метод, метод отклонений и т.п.
Выборочное и сплошное наблюдение. Проведение сплошных и выборочных наблюдений широко применяется в экономическом анализе работы предприятия. Примером сплошных наблюдений в изучении экономики могут быть полные инвентаризации основных средств, складских запасов материалов и т.д. Выборочными наблюдениями являются проводимые на предприятиях «фотографии» рабочего дня, работы оборудования, смотры резервов в производстве и т.п. Объектом наблюдения являются в данном случае не все рабочие места, или станки, а лишь их часть. По данным выборочных наблюдений на основе методов теории вероятностей определяется возможность распространения выводов на всю совокупность изучаемых явлений. Например, по выборочным «фотографиям» рабочего места судят об использовании рабочего времени в цехе, на заводе.
Сравнения – важнейший метод экономического анализа, позволяющий выразить характеристику явления через другие однородные явления. В широком смысле слово сравнение присуще каждому экономическому расчету. Мы же рассматриваем сравнение как аналитический прием, позволяющий выявить взаимосвязь экономических явлений, их развитие и степень достижения эффективности в использовании материальных, трудовых и финансовых ресурсов.
Основные виды сравнений:
∙ сравнение отчетных показателей с плановыми – позволяет выявить причины невыполнения плановых заданий по отдельным показателям и наметить мероприятия для улучшения работы предприятия в дальнейшем;
∙ сравнение отчетных показателей с показателями предшествующих периодов – показывает темпы роста производства, динамику показателей, тенденцию развития производства;
∙ межхозяйственные сравнения, т.е. сравнение показателей предприятия с показателями других предприятий, - позволяет вскрыть многие резервы, перенять передовой опыт. Межхозяйственные сравнения конкурентов получили широкое распространение в экономическом анализе и практически выделились в самостоятельный вид анализа – так называемый межхозяйственный сравнительный анализ. В условиях рыночной экономики сравнительный анализ работы предприятий-конкурентов является объективной необходимостью для повышения эффективности и выживаемости в конкурентной борьбе. Можно проводить сравнение не только родственных предприятий. Финансовые коэффициенты, взятые во всеобщей денежной оценке, позволяют найти общий знаменатель для сравнения качества работы предприятий разных отраслей;
∙ сравнение со среднеотраслевыми данными – позволяет определять, соответствуют ли индивидуальные затраты на данном предприятии общественно необходимым; установить организационно-технический уровень предприятия и место, занимаемое им в ряду других предприятий данной отрасли;
∙ сравнение показателей предприятия со средними показателями рыночной экономики – в основном в форме финансовых коэффициентов.
Использование приема сравнения предполагает сопоставимость сравниваемых показателей: единство оценки, сравнимость календарных сроков, устранение влияния различий в объеме и ассортименте в отдельных случаях, сезонных особенностей и территориальных различий, географических условий, различий в методике расчета показателей и т.д. Перечисленные виды сравнения являются основными, но при изучении экономики используется много других видов сравнения.
Графический метод. В экономическом анализе графики являются не только средством иллюстрации хозяйственных процессов, но и методом изучения экономики, который, однако, слабо разработан. Значение графического метода в анализе повышается в связи с расширением сферы изучения экономики на предприятиях не только менеджерами, но и общественностью.
В экономике связь между экономическими явлениями и показателя находит свое количественное выражение – например, чем выше производительность труда рабочего и чем их больше, тем больше выпуск продукции. Такую зависимость, когда изменение одних величин обусловливает изменение других, называют функциональной.
Связь между переменными можно выразить тремя способами: таблицей, формулой и графиком. Табличный способ задания функции состоит в том, что значения функции, отвечающие определенным значениям аргумента или аргументов, приводятся в виде таблиц. Способ выражения зависимости с помощью формулы (уравнения) называется аналитическим. Наконец, при графическом способе зависимость между показателями изображается при помощи диаграммы (графика). В экономическом анализе для изображения функции одного аргумента пользуются в основном прямоугольными координатами.
Исходной базой экономического анализа являются данные бухгалтерского учета и отчетности, аналитический просмотр которых должен восстановить все основные аспекты хозяйственной деятельности и совершенных операций в обобщенной форме, т.е. с необходимой для анализа степенью агрегирования.
Практика анализа выработала основные методы чтения финансовых отчетов. Среди них можно выделить следующие стандартные приемы, которые будут рассмотрены в соответствующих лекциях учебного курса:
∙ анализ абсолютных данных;
∙ горизонтальный анализ;
∙ вертикальный анализ;
∙ трендовый анализ;
∙ метод финансовых коэффициентов.
В практике экономического анализа активно используются различные количественные методы, которые разделяются на статистические, бухгалтерские и экономико-математические.
Экономико-математические методы анализа. В экономическом анализе придается большое значение математическим методам, моделям, формулам, но эти методы, модели и формулы не могут заменить и подменить теоретический анализ сущности экономических явлений и процессов. Как указывал английский естествоиспытатель Т.Г.Гексли, математика, подобно жернову, перемалывает то зерно, которое засыпают, и как, засыпав лебеду, вы не получите пшеничной муки, так, исписав целые страницы формулами, вы не получите истины из ложных предпосылок.
Проникновение математики и компьютеров в экономический анализ – объективный процесс. Происходит обогащение экономического анализа. Систематизировать применяемые в анализе хозяйственной деятельности математические методы можно по различным признакам. Наиболее целесообразной представляется классификация экономико-математических методов по содержанию метода, т.е. принадлежности к определенному разделу современной математики.
Методы элементарной математики используются в обычных традиционных экономических расчетах при обосновании потребностей в ресурсах, учете затрат на производство, обосновании планов, проектов, балансовых расчетов и т.д.
Классические методы математического анализа применяются не только в рамках других методов, например, методов математической статистики и математического программирования, но и отдельно. Так, факторный анализ изменения многих экономических показателей может быть осуществлен при помощи дифференцирования и других разработанных на базе дифференцирования методов.
Широкое распространение в экономическом анализеимеют методы математической статистики и теории вероятностей. Эти методы применяются в тех случаях, когда изменение анализируемых показателей можно представить как случайный процесс.
Статистические модели как основное средство изучения массовых, повторяющихся явлений играют важную роль в прогнозировании поведения экономических показателей. Когда связь между анализируемыми характеристиками не детерминированная, а стохастическая, то статистические и вероятностные методы – практически единственный инструмент исследования. Наибольшее распространение из математико-статистических методов в экономическом анализе получили методы множественного и парного корреляционного анализа.
Для изучения одномерных статистических совокупностей используются: вариационный ряд, законы распределения, выборочный метод; а для изучения многомерных статистических совокупностей корреляции, регрессии – дисперсионный и статистический факторный анализ.
Эконометрические методы строятся на синтезе трех областей знаний: экономики, математики и статистики. Основа эконометрии – экономическая модель, т.е. схематическое представление экономического явления или процесса при помощи научной абстракции, отражения их характерных черт. Наибольшее распространение получил метод анализа «затраты-выпуск». Это матричные (балансовые) модели, строящиеся по шахматной схеме и позволяющие в наиболее компактной форме представить взаимосвязь затрат и результатов производства. Удобство расчетов и четкость экономической интерпретации – главные особенности матричных моделей, важные при создании систем компьютерной обработки данных.
Математическое программирование – важный раздел современной прикладной математики. Методы математического (прежде всего линейного) программирования служат основным средством решения задач оптимизации производственно-хозяйственной деятельности. По своей сути эти методы есть средство плановых расчетов. Их ценность для экономического анализа выполнения плана в том, что они позволяют оценивать напряженность плановых заданий, определять лимитирующие группы оборудования, виды сырья и материалов, получать оценки дефицитности произведенных ресурсов и т.п.
Под исследованием операций подразумеваются разработка методов целенаправленных действий (операций), количественная оценка полученных решений и выбор наилучшего из них. Предметом исследования операций являются экономические системы, в том числе хозяйственная деятельность предприятий. Цель – такое сочетание структурных взаимосвязанных элементов систем, которое в наибольшей степени отвечает задаче получения наилучшего экономического показателя из ряда возможных.
Экономическая кибернетика позволяет анализировать экономические явления и процессы в качестве очень сложных систем с точки зрения законов и механизмов управления и движения информации в них. Наибольшее распространение в экономическом анализе получили методы кибернетического моделирования и системного анализа.
Математическая теория оптимальных процессов применяется для управления технико-экономическими процессами и ресурсами.
Эвристические методы (решения) – это неформализованные методы решения аналитических задач, связанные с опросом и экспертными оценками специалистов, высказывающих свое мнение на основе интуиции, опыта, с математической обработкой разных мнений для нахождения правильного решения.
Экономико-математическое моделирование. Применение математики в экономике принимает форму экономико-математического моделирования. С помощью экономико-математической модели изображается тот или иной действующий экономический процесс. Такая модель может быть сконструирована только на основе глубокого теоретического исследования экономической сущности процесса. Только в этом случае математическая модель будет адекватна действительному экономическому процессу, будет объективно отражать его.
В экономическом анализе используются главным образом математические модели, описывающие изучаемое явление или процесс с помощью уравнений, неравенств, функций и других математических средств. Различают математические модели:
∙ с количественными характеристиками, записанными в виде формул;
∙ числовые модели с конкретными числовыми характеристиками;
∙ логические, записанные с помощью логических выражений, и
∙ графические, выраженные в графических образах.
Модели, реализованные с помощью ЭВМ, называют машинными или электронными.
Таким образом, экономико-математическое моделирование работы предприятия должно быть основано на анализе деятельности и обогащать этот анализ результатами и выводами, полученными после решения соответствующих задач.
Построение, или моделирование, конечной факторной системы для анализируемого экономического показателя хозяйственной деятельности может быть осуществлено как формальным, так и эвристическим путем на основе качественного анализа сущности экономического явления, отражаемого через данный результативный показатель. Моделирование факторной системы основывается на следующих экономических критериях выделения факторов как элементов факторной системы: причинность, достаточная специфичность, самостоятельность существования, учетная возможность. С формальной точки зрения факторы, включаемые в факторную систему, должны быть количественными и измеримыми.
В детерминированном моделировании факторных систем можно выделить небольшое число типов конечных факторных систем, наиболее часто встречающихся в анализе хозяйственной деятельности, где ∑ - сумма, Π – произведение факторов:
∙ аддитивные модели:
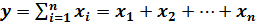 ,
,
∙ мультипликативные модели:
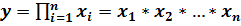 ,
,
∙ кратные модели:
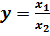 ,
, 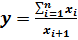 ,
, 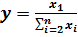 ,
, 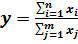 ,
,
где y – результативный показатель (исходная факторная система);
xi и xj – факторы (факторные показатели).
Применительно к классу детерминированных факторных систем различают следующие основные приемы моделирования:
1. Метод удлинения факторной системы. Исходная факторная система y=a1/a2. Если a представить в виде суммы отдельных слагаемых-факторов
a1=a11+a12+a13+…+a1n , то 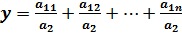 – конечная факторная система вида
– конечная факторная система вида
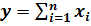 .
.
2. Метод расширения факторной системы. Исходная факторная система y=a1/a2. Если и числитель, и знаменатель дроби «расширить» умножением на одно и то же число, то получим новую факторную систему:
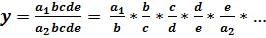 , т.е. мультипликативную модель вида
, т.е. мультипликативную модель вида 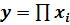 .
.
3. Метод сокращения факторной системы. Исходная факторная система y=a1/a2. Если и числитель, и знаменатель дроби разделить на одно и то же число, то получим новую факторную систему (при этом, естественно, должны быть соблюдены правила выделения факторов):
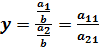 .
.
В данном случае имеем конечную факторную систему вида y=x1/x2.
Таким образом, сложный процесс формирования уровня изучаемого показателя хозяйственной деятельности может быть разложен с помощью различных приемов на составляющие (факторы) и представлен в виде модели детерминированной факторной системы.
Основу детерминированного моделирования факторной системы составляет возможность построения тождественного преобразования для исходной формулы экономического показателя с другими показателями-факторами. Детерминированное моделирование факторных систем – простое и эффективное средство формализации связи экономических показателей; оно служит основой для количественной оценки роли отдельных факторов в динамике изменения обобщающего показателя.
Детерминированное моделирование факторных систем ограничено длиной факторного поля прямых связей. При недостаточном уровне знаний о природе прямых связей того или иного показателя хозяйственной деятельности часто необходим иной подход к познанию объективной действительности. Размах количественных изменений экономических показателей можно выяснить только методами стохастического моделирования массовых эмпирических данных.
Стохастический анализ направлен на изучение косвенных связей, т.е. опосредованных факторов (в случае невозможности определения непрерывной цепи прямой связи). Из этого следует важный вывод о соотношении детерминированного и стохастического анализа: так как прямые связи необходимо изучать в первую очередь, то стохастический анализ носит вспомогательный характер. Стохастический анализ выступает в качестве инструмента углубления детерминированного анализа факторов, по которым нельзя построить детерминированную модель.
Корреляционно-регрессионный анализ – классический метод стохастического моделирования хозяйственной деятельности. Он изучает взаимосвязи показателей хозяйственной деятельности, когда зависимость между ними не является строго функциональной и искажена влиянием посторонних, случайных факторов. При проведении корреляционно-регрессионного анализа строят различные корреляционные и регрессионные модели хозяйственной деятельности. В этих моделях выделяют факторные и результативные показатели (признаки). В зависимости от количества исследуемых показателей различают парные и многофакторные модели корреляционно-регрессион-ного анализа.
Основной задачей корреляционно-регрессионного анализа является выяснение формы и тесноты связи между результативным и факторным показателями. Под формой связи понимают тип аналитической формулы, выражающей зависимость результативного показателя от изменений факторного. Существует прямая связь, когда с ростом (снижением) значения факторного показателя наблюдается тенденция к росту (снижению) значений результативного показателя. В противном случае между показателями существует обратная связь. Форма связи может быть прямолинейной (ей соответствует уравнение прямой линии), когда наблюдается тенденция равномерного возрастания или убывания результативного показателя, в противном случае форма связи называется криволинейной (ей соответствует уравнение параболы, гиперболы и др.).
Основные модели корреляционного анализа: коэффициент парной корреляции, коэффициент частной корреляции, коэффициент множественной корреляции, коэффициент детерминации.
Современный факторный анализ – направление многомерного статистического анализа, которое позволяет выявить внутренние, непосредственно неизмеримые переменные (факторы) между коррелирующими показателями хозяйственной деятельности. Различают два основных метода современного факторного анализа: метод главных компонент и классический факторный анализ.
Методы детерминированного факторного анализа. В анализе хозяйственной деятельности, который иногда называют бухгалтерским, преобладают методы детерминированного моделирования факторных систем, которые дают точную (а не с некоторой вероятностью, характерной для стохастического моделирования) сбалансированную характеристику влияния факторов на изменение результативного показателя. Но достигается эта сбалансированность разными методами. Рассмотрим основные методы детерминированного факторного анализа.
Метод дифференциального исчисления является теоретической основой для количественной оценки роли отдельных факторов в динамике результативного (обобщающего) показателя.
Метод дифференциального исчисления основан на формуле полного дифференциала. Для функции от двух переменных z=f(x,y) имеем полное приращение функции ∆z:
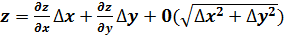 ,
,
где ∆x, ∆y – факторные приращения соответствующих переменных;
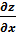 ,
, 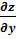 – частные производные;
– частные производные;
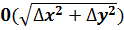 – бесконечно малая величина более высокого порядка, чем
– бесконечно малая величина более высокого порядка, чем 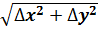 . Эта величина в расчетах отбрасывается (ее часто обозначают как ε).
. Эта величина в расчетах отбрасывается (ее часто обозначают как ε).
Таким образом, влияние фактора х на обобщающий показатель определяется по формуле:
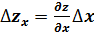 ,
,
а влияние фактора y – по формуле:
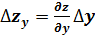 .
.
В методике дифференциального исчисления предполагается, что общее приращение функций (результирующего показателя) разлагается на слагаемые, и значение каждого из них определяется как произведение соответствующей гибкой производной на приращение переменной (фактора), по которой исчислена данная производная. В этом методе так называемый неразложимый остаток, который интерпретируется как логическая ошибка метода дифференцирования, просто отбрасывается. В этом состоит «неудобство» дифференцирования для экономических (особенно бухгалтерских) расчетов, в которых, как правило, требуется точный баланс изменения результативного показателя и алгебраической суммы влияния всех факторов.
Индексный метод определения влияния факторов на обобщающий показатель применяется в статистике, планировании и анализе хозяйственной деятельности как основа для количественной оценки роли отдельных факторов в динамике изменений обобщающих показателей.
Так, изучая зависимость объема выпуска продукции на предприятии от изменений численности работающих и производительности труда, можно воспользоваться следующей системой взаимосвязанных индексов:
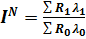 , (3.1)
, (3.1)
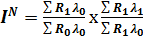 , (3.2)
, (3.2)
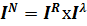 , (3.3)
, (3.3)
где IN – общий индекс изменения объема продаж продукции;
IR – индивидуальный (факторный) индекс изменения численности работающих;
Iλ – факторный индекс изменения производительности труда работающих;
R0, R1 – среднегодовая численность персонала соответственно в базисном и отчетном периодах;
λ0, λ1 – среднегодовая продажа продукции на одного работающего соответственно в базисном и отчетном периодах.
Приведенные формулы показывают, что общее относительное изменение объема продукции образуется как произведение относительных изменений двух факторов – численности работающих и производительности их труда. Формулы отражают принятую в статистике практику построения факторных индексов, суть которой можно сформулировать следующим образом:
Если обобщающий экономический показатель представляет собой произведение количественного (объемного) и качественного показателей-факторов, то при определении влияния количественного фактора качественный показатель фиксируется на базисном уровне, а при определении влияния качественного фактора количественный показатель фиксируется на уровне отчетного периода.
Индексный метод позволяет провести разложение по факторам не только относительных, но и абсолютных отклонений обобщающего показателя.
В нашем примере формула (3.1) позволяет вычислить величину абсолютного отклонения (прироста) обобщающего показателя – объема продаж продукции предприятия:
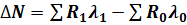 ,
,
где ∆N – абсолютный прирост объема продаж продукции в анализируемом периоде.
Это отклонение образовалось под влиянием изменений численности работающих и производительности их труда. Чтобы определить, какая часть общего изменения объема продаж продукции достигнута за счет изменения каждого из факторов в отдельности, необходимо при расчете влияния одного из них элиминировать влияние другого фактора.
Формула (3.2) соответствует данному условию: в первом сомножителе элиминировано влияние производительности труда, во втором – численности работающих. Следовательно, прирост объема продукции за счет изменения численности работающих определяется как разность между числителем и знаменателем первого сомножителя:
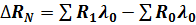 .
.
Прирост выпуска продукции за счет изменения производительности труда работающих определяется аналогично по второму сомножителю:
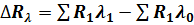 .
.
Этот принцип разложения абсолютного прироста (отклонения) обобщающего показателя по факторам пригоден для случая, когда число факторов равно двум (один из них количественный, другой – качественный), а анализируемый показатель представлен как их произведение.
Теория индексов не дает общего метода разложения абсолютных отклонений обобщающего показателя по факторам при наличии более двух факторов и если их связь не является мультипликативной.
Метод цепных подстановок заключается в получении ряда промежуточных значений обобщающего показателя путем последовательной замены базисных значений факторов на фактические. Разность двух промежуточных значений обобщающего показателя в цепи подстановок равна изменению обобщающего показателя, вызванного изменением соответствующего фактора.
В общем виде имеем следующую систему расчетов по методу цепных подстановок:
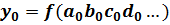 – базисное значение обобщенного показателя;
– базисное значение обобщенного показателя;
(факторы)
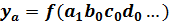 – промежуточное значение;
– промежуточное значение;
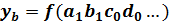 – промежуточное значение;
– промежуточное значение;
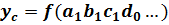 – промежуточное значение;
– промежуточное значение;
 ;
;
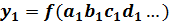 – фактическое значение.
– фактическое значение.
Общее абсолютное отклонение показателя определяется по формуле:
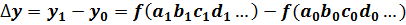 .
.
Общее отклонение обобщающего показателя раскладывается на факторы:
∙ за счет изменения фактора а:
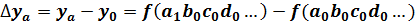 ;
;
∙ за счет изменения фактора b:
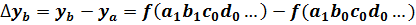 ;
;
и т.д.
метод цепных подстановок, как и индексный, имеет недостатки. Во-первых, результаты расчетов зависят от последовательности замены факторов; во-вторых, активная роль в изменения обобщающего показателя необоснованного часто приписывается влиянию изменения качественного фактора.
Например, если исследуемый показатель z имеет вид функции z=f(x,y)=xy, то его изменение за период ∆t=t1-t0 выражается формулой:
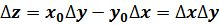 ;
;
где ∆t – приращение обобщающего показателя;
∆x, ∆y – приращение факторов;
x0, y0 – базисные значения факторов;
to, t1 – соответственно базисный и отчетный период времени.
Группируя в этой формуле последнее слагаемое с одним из первых, получаем два различных варианта цепных подстановок:
∙ первый вариант:
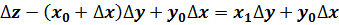 ;
;
∙ второй вариант:
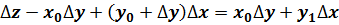 .
.
На практике обычно применяется первый вариант при условии, что х - количественный фактор, а у – качественный.
В этой формуле выявляется влияние качественного фактора на изменение обобщающего показателя, т.е. выражение (х0+∆х)∆у более активно, поскольку величина его устанавливается умножением приращения качественного фактора на отчетное значение количественного фактора. Тем самым весь прирост обобщающего показателя за счет совместного изменения факторов (ε) приписывается влиянию только качественного фактора. Таким образом, задача точного определения роли каждого фактора в изменении обобщающего показателя обычным методом цепных подстановок не решается.
Интегральный метод факторного анализа основан на суммировании приращений функции, определенной как частная производная, умноженная на приращение аргумента на бесконечно малых промежутках.
Интегральный метод дает наиболее общий подход к решению задач факторного анализа по разложению общего прироста показателя по факторным приращениям. Основу интегрального метода составляет интеграл Эйлера-Лагранжа, устанавливающий связь между приращением функции и приращением факторных признаков. Для функции z=f(x,y) имеем следующие формулы расчета факторных влияний:
∙ по методу дифференцирования:
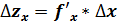 – влияние фактора х;
– влияние фактора х;
где f'x – частная производная функция по х;
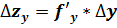 – влияние фактора y;
– влияние фактора y;
где f'y – частная производная функция по y;
∙ по интегральному методу:
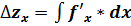 – влияние фактора х;
– влияние фактора х;
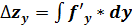 – влияние фактора y.
– влияние фактора y.
Интегральный метод дает точные оценки факторных влияний. Результаты расчетов не зависят от последовательности подстановок и последовательности расчета факторных влияний. Метод применим для всех видов непрерывно дифференцируемых функций; не требует предварительных знаний о том, какие факторы являются количественными, а какие – качественными.
Для применения интегрального метода требуются знание основ дифференциального исчисления, техники интегрирования и умение находить производные различных функций. Вместе с тем в теории анализа хозяйственной деятельности для практических приложений разработаны конечные рабочие формулы интегрального метода[8] для наиболее распространенных видов факторных зависимостей, что делает этот метод доступным для каждого аналитика. Приведем некоторые из них:
1. Факторная модель типа u=xy:
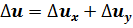 ;
;
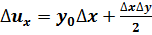 ;
;
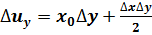 ;
;
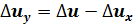 .
.
2. Факторная модель типа u=xyz:
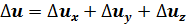 ;
;
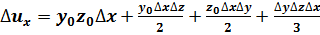 ;
;
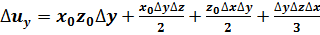 ;
;
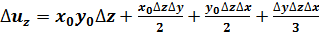 .
.
3. Факторная модель типа u=x/y:
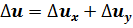 ;
;
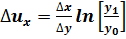 ;
;
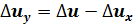 .
.
4. Факторная модель типа u=x/(y+z):
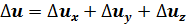 ;
;
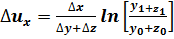 ;
;
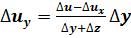 ;
;
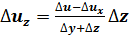 .
.
На рис.3.1 приведен пример использования основных методов факторного анализа на основе показателей предприятия за два года (см. Приложение 4). Рассматривается двухфакторная мультипликативная модель N=R*λ, где N – продажа продукции; R – производственный персонал; λ – производительность труда.
Продажа первого года составила: N0=R0*λ0 = 381*209 186 = 79 700 (тыс.руб.).
Продажа второго года - соответственно: N1=R1*λ1 = 382*218 874 = 83 610 (тыс.руб.).
Отклонение продажи второго года от первого года составило: ∆N=N1-N0 = 83 610 – 79 700 = 3 910 (тыс.руб.).
Задача - разложить это отклонение в зависимости от влияния двух рассматриваемых факторов. Схема и расчеты основных методов экономического факторного анализа приведены ниже.
Прямоугольник А на схеме означает продукцию первого года [N0=R0*λ0 = 79 700 (тыс.руб.)];
большой прямоугольник В – продукцию второго года [N1=R1*λ1 = 83 610 (тыс.руб.)];
прямоугольник С – приращение продукции за счет фактора численности персонала, рассчитанное методом дифференциального исчисления [∆NR-∆λ*R0=209,2 (тыс.руб.)];
прямоугольник D – приращение продукции за счет фактора производительности труда, также рассчитанное методом дифференциального исчисления [∆Nλ-∆λ*R0 =369,1 (тыс.руб.)];
прямоугольник Е – ε, т.е. бесконечно малую величину при дифференцировании [ε=∆R*∆λ = 9,7 (тыс.руб.)].
Таким образом, продукция второго года превышает продукцию первого года на три величины: B – A = C + D + E, а B = A + B + C + E.
Метод дифференциального исчисления разлагает приращение продукции на три элемента: ∆N = C + D + E.
Индексный метод разлагает приращение продукции на два элемента: ∆N = (D + E) + C.
R0=381 человек R1=382 человек
∆R=1
1. Метод дифференциального исчисления:
∆N = ∆NR + ∆Nλ + ε = ∆R * λ0 + ∆λ * R0 + ∆R * ∆λ = 209,2 + 3 691,1 + 9,7 = 3 910 (тыс.руб.);
2. Индексный метод:
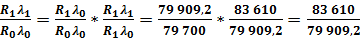 ;
∙ влияние в коэффициентах:
1,003 * 1,046 = 1,049;
∙ влияние в абсолютных цифрах:
∆NR = 79 909,2 - 79 700 = 209,2 (тыс.руб.) ;
∆Nλ = 83 610 - 79 909,2 = 3 700,8 (тыс.руб.) ;
3. Метод цепных подстановок;
1-й вариант: N0 = R0*λ0 ∆NR = R1*λ0 – R0*λ0 = 79 909,2 – 79 700 = 209,2 (тыс.руб.);
NR = R1*λ0
N1 = R1*λ1 ∆Nλ = R1*λ1 – R1*λ0 = 83 610 – 79 909,2 = 3 700,8 (тыс.руб.);
2-й вариант: N0 = R0*λ0 ∆Nλ = R0*λ1 – R0*λ0 = 83 391 – 79 700 = 3 691 (тыс.руб.);
Nλ = R0*λ1
N1 = R1*λ1 ∆NR = R1*λ1 – R0*λ1 = 83 610 – 83 391 = 219 (тыс.руб.);
4. Интегральный метод:
∆N = ∆NR + ∆Nλ ;
∆NR = ∆R * λ0 + ∆R * ∆λ / 2 = 1 * 209,2 + (1 * 9,7) / 2 = 209,2 + 4,85 = 214,05 (тыс.руб.);
∆Nλ = ∆λ * R0 + ∆R * ∆λ / 2 = 9,7 * 381 + (1 * 9,7) / 2 = 3 691,1 + 4,85 = 3 695,95 (тыс.руб.). ;
∙ влияние в коэффициентах:
1,003 * 1,046 = 1,049;
∙ влияние в абсолютных цифрах:
∆NR = 79 909,2 - 79 700 = 209,2 (тыс.руб.) ;
∆Nλ = 83 610 - 79 909,2 = 3 700,8 (тыс.руб.) ;
3. Метод цепных подстановок;
1-й вариант: N0 = R0*λ0 ∆NR = R1*λ0 – R0*λ0 = 79 909,2 – 79 700 = 209,2 (тыс.руб.);
NR = R1*λ0
N1 = R1*λ1 ∆Nλ = R1*λ1 – R1*λ0 = 83 610 – 79 909,2 = 3 700,8 (тыс.руб.);
2-й вариант: N0 = R0*λ0 ∆Nλ = R0*λ1 – R0*λ0 = 83 391 – 79 700 = 3 691 (тыс.руб.);
Nλ = R0*λ1
N1 = R1*λ1 ∆NR = R1*λ1 – R0*λ1 = 83 610 – 83 391 = 219 (тыс.руб.);
4. Интегральный метод:
∆N = ∆NR + ∆Nλ ;
∆NR = ∆R * λ0 + ∆R * ∆λ / 2 = 1 * 209,2 + (1 * 9,7) / 2 = 209,2 + 4,85 = 214,05 (тыс.руб.);
∆Nλ = ∆λ * R0 + ∆R * ∆λ / 2 = 9,7 * 381 + (1 * 9,7) / 2 = 3 691,1 + 4,85 = 3 695,95 (тыс.руб.).
|
| B D ∆N1=9,7*381=3 691,1 (тыс.руб.) Е 9,7*1=9,7 (тыс.руб.) Λ0=209,2 (тыс.руб.) А N0=R0*λ0=79 700 (тыс.руб.) С ∆NR=209,2*1=209,2 (тыс.руб.) ∆λ=9,7 (тыс.руб.) N1=R1*λ1=83 610 (тыс.руб.) Λ1=218,9 (тыс.руб.) ∆N=3 910 (тыс.руб.) |
Рис.3.1. Иллюстрация методов факторного анализа.
Метод цепных подстановок разлагает приращение продукции на два элемента, но при рассмотрении двухфакторной мультипликативной модели возможны два варианта расчетов: ∆N = (D + E ) + C или ∆N = D + (C + E) – в зависимости от порядка подстановок.
При рассмотрении трехфакторной функции уже возможны шесть вариантов результата и т.д. (т.е. n! вариантов результатов).
Интегральный метод дает всегда однозначный результат, в данном примере ∆N = (C + E / 2) + (D + E / 2).
Классификация задач экономического анализа. Задачи экономического анализа могут классифицироваться по разным признакам.
По квалификационному признаку оптимальности все задачи (методы) подразделяются на оптимизационные и неоптимизационные.
По признаку получения точного решения все задачи подразделяются на точные и приближенные.
Особое значение в анализе хозяйственной деятельности имеет группировка задач на балансовые и факторные.
Балансовые задачи (методы) – это анализ структуры, пропорций, соотношений (анализ финансового состояния по данным бухгалтерского баланса, анализ денежных потоков, анализ баланса материальных ресурсов и т.д.).
Наибольший удельный вес задач экономического анализа решаются методами факторного анализа (примерно 90% задач приходится на факторный анализ и лишь 10% - на балансовый анализ).
Под экономическим факторным анализом понимаются постепенные переход от исходной факторной модели (результативный показатель) к конечной факторной модели (или наоборот), раскрытие полного набора количественно измеримых факторов, влияющих на изменение результативного показателя.
Примерная классификация задач факторного анализа приведена на рис.3.2.
| Ретроспективный анализ |
| Перспективный анализ |
| Оперативный анализ |
| Пространственный анализ |
| Временной анализ |
| Статический анализ |
| Динамический анализ |
| Одноступенчатый анализ |
| Цепной анализ |
| Детерминированный факторный анализ |
| Стохастический анализ |
| Прямой факторный анализ |
| Обратный факторный анализ (синтез) |
| Экономический факторный анализ |
Рис.2.2. Классификация задач экономического факторного анализа.
При проведении прямого факторного анализа выявляются отдельные факторы, влияющие на изменение результативного показателя или процесса, устанавливаются формы детерминированной (функциональной) или стохастической зависимости между результативным показателем и определенным набором факторов и выясняется роль отдельных факторов в изменении результативного экономического показателя.
Постановка задачи прямого факторного анализа распространяется на детерминированные и стохастические случаи.
Пусть y=f(x) – некоторая функция, характеризующая изменение результативного показателя или процесса; x1, x2, …, xn – факторы, от которых зависит функция f(xi). Задана функциональная детерминированная форма связи изучаемого показателя y с набором факторов x1, x2, …, xn: y=f(x1, x2, …, xn). Пусть показатель y получил приращение (∆y) за анализируемый период. Требуется определить, какая часть численного приращения функции y=f(x1, x2, …, xn) обусловлена приращением каждого аргумента (фактора). Сформулированная таким образом задача есть постановка прямого детерминированного факторного анализа.
Примерами прямого детерминированного факторного анализа являются:
∙ анализ влияния производительности труда и численности работающих на объем продукции (y – объем продукции; x, z – факторы; задана функциональная форма связи y=xz);
∙ анализ влияния величины прибыли, стоимости основных производственных фондов и нормируемых оборотных средств на уровень рентабельности (y – уровень рентабельности; x, z, v – соответствующие факторы; заданная функциональная форма связи y=x/(z+v)).
Задачи прямого детерминированного факторного анализа являются наиболее распространенными в анализе хозяйственной деятельности.
Рассмотрим особенности постановки задачи прямого стохастического факторного анализа. Если в случае прямого детерминированного факторного анализа исходные данные для анализа имеются в форме конкретных чисел, то в случае прямого стохастического факторного анализа они заданы выборкой (временной или поперечной). Решение задач стохастического факторного анализа требуют глубокого экономического исследования для выявления основных факторов, влияющих на результативный показатель; подбора вида регрессии, которой бы наилучшим образом отражал действительную связь изучаемого показателя с набором факторов; разработки метода, позволяющего определить влияние каждого фактора на результативный показатель. Если результаты прямого детерминированного анализа должны получиться точными и однозначными, то результаты стохастического – с некоторой вероятностью (надежностью), которую следует оценить.
Примером стохастического факторного анализа является регрессионный анализ производительности труда и других экономических показателей.
В экономическом анализе кроме задач детализации показателя, разбивки его на составляющие части существует группа задач синтеза, требующих увязать ряд экономических характеристик в комплексе, т.е. построить функцию, содержащую основное качество всех рассматриваемых экономических показателей-аргументов. Иными словами, в данном случае ставится обратная задача (относительно задачи прямого факторного анализа) – объединения ряда показателей в комплекс.
Пусть имеется набор показателей x1, x2, …, xn, характеризующих некоторый экономический процесс (L). Требуется построить функцию f(xi) изменения процесса L, содержащую в себе основные характеристики всех показателей x1, x2, …, xn, или некоторых из них в комплексе. В зависимости от цели исследования функция f(xi) должна характеризовать процесс в статике или в динамике. Данная постановка задачи называется задачей обратного факторного анализа.
Задачи обратного факторного анализа могут быть детерминированными (например, задачи комплексной оценки хозяйственной деятельности, а также задачи математического программирования, в том числе и линейного) и стохастического (например, производственные функции, которыми устанавливаются зависимости между величиной продукции и затратами производственных факторов первичных ресурсов).
Для детального исследования экономических показателей или процессов необходимо проводить не только одноступенчатый, но и цепной факторный анализ: статический (пространственный) и динамический (пространственный и во времени).
Пусть исследуется экономический показатель y; x1, x2, …, xn – факторы, влияющие на этот показатель. В зависимости от цели исследования анализируется поведение показателя y одним из методов факторного анализа. Если x1, x2, …, xn – функции более детальных факторов, то для анализа y надо объяснить поведение x1, x2, …, xn. Для этого проводят дальнейшую детализацию.
Закончив ее, решают обратную задачу факторного анализа, синтезируя результаты исследования для характеристики результативного показателя y. Такой метод исследования называется цепным статическим методом факторного анализа.
При использовании цепного динамического факторного анализа для полного изучения поведения результативного показателя недостаточно его статического значения: факторный анализ показателя проводится на различных интервалах дробления времени, на которых исследуется показатель.
Экономический факторный анализ может быть направлен на выяснение действия факторов, формирующих результаты хозяйственной деятельности, по различным источникам пространственного и временного происхождения.
Анализ динамических (временных) рядов показателей хозяйственной деятельности, расщепление уровня ряда на его составляющие (основную линию развития – тренд; сезонную, или периодическую, составляющую; циклическую составляющую, связанную с воспроизводственными явлениями; случайную составляющую) – задача временного факторного анализа.
Классификация задач факторного анализа упорядочивает постановку многих экономических задач, позволяет выявить общие закономерности в их решении. При исследовании сложных экономических процессов возможна комбинация постановки задач, если последние не относятся целиком к какому-либо типу, указанному в классификации.
Дата добавления: 2015-10-09; просмотров: 4433;
