Теоретическое введение. Рассмотрим процесс заряда конденсатора в электрической цепи, содержащей последовательно соединенные конденсатор С

Рассмотрим процесс заряда конденсатора в электрической цепи, содержащей последовательно соединенные конденсатор С, сопротивление R и источник ЭДС ε (рис. 6.1). Первоначально конденсатор не заряжен. Пусть I, q, U – мгновенные значения тока, заряда и разности потенциалов между обкладками конденсатора. Полагаем, что токи и напряжения удовлетворяют условиям квазистационарности, т.е. мгновенное значение тока во всех сечениях провода и элементах цепи (рис. 6.1) одно и то же, и соотношение между мгновенными значениями I, q и U такое же, как и в цепи постоянного тока. В момент времени t=0 ключ К замкнули, и в цепи пошел ток, заряжающий конденсатор 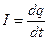, где q – заряд конденсатора. Применим закон Ома к цепи (рис. 6.1):

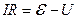, (6.1)

где R – полное сопротивление цепи, включающее внутреннее сопротивление источника ЭДС. Учитывая, что разность потенциалов на пластинах конденсатора U=q/C, запишем предыдущее уравнение в виде

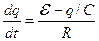, (6.2)

Разделим переменные и проинтегрируем это уравнение с учетом начального условия: при t=0, q=0:

;

;

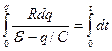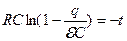Откуда

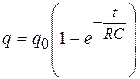, (6.3)

Напряжение на конденсаторе изменяется по закону

,

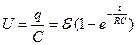закон изменения тока в цепи получим дифференцированием:

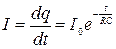, (6.4)

где 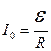. Графики зависимостей q(t) и I(t) представлены на рис. 6.2.

Рассмотрим процесс разряда конденсатора емкостью С, пласти­ны которого замкнуты сопротивлением R. Пусть dq – уменьшение заряда конденсатора за время dt. При разряде конденсатора в це­пи (рис. 6.3) протекает ток 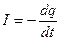. Известно, что 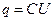, где U – разность потенциалов на конденсаторе, а следовательно, и на сопротивлении R . По закону Ома имеем U=IR , тогда

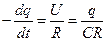, (6.5)

Уравнение (6.5) показывает, что скорость уменьшения заряда конден­сатора пропорциональна величине этого заряда. Интегрируя уравнение (6.5) при условии, что в момент времени t=0 q=q₀, получим

,

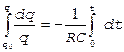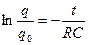, (6.6)

откуда

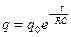, (6.7)

Функция q(t) называется экспоненциальной. График зависимости q(t) приведен на рис. 6.4. Закон изменения напряжения на конденсаторе в процессе разряда аналогичен (6.7):

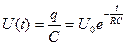, (6.8)

где 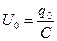. Произведение RС имеет размерность времени ( 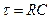) и назы­вается постоянной времени, или временем релаксации 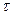. За время 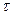заряд конденсатора уменьшается в e раз. Для определения RС часто удобно измерять время, за которое величина заряда падает до поло­вины первоначального значения, так называемое "половинное время" t_1/2. "Половинное время" определяется из выражения

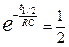, (6.9)

Взяв натуральный логарифм от обеих частей уравнения (6.9), получа­ем 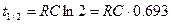, или

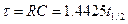(6.10)

Способ измерения постоянной времени состоит в определении t_1/2 и умножении полученной величины на 1.44. Так как экспонента асимптотически приближается к оси абсцисс, то точно установить окончание процесса разряда конденсатора (так же как и процесса заряда) не представляется возможным. Поэтому целесообразно изме­рять время уменьшения величины заряда в 2 раза, т.е. “половинное время”. За каждый интервал времени t_1/2=0.693ּRC заряд на емкости уменьшается в два раза (рис. 6.5).

Кроме того, постоянную времени можно найти графическим способом. Из формулы (6.8) находим:

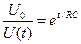, (6.11)

Логарифмируя левую и правую части формулы (6.11), получаем

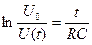. (6.12)

Построив логарифмическую зависимость, y=f(x), где 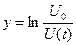, а , получим прямую, котангенс угла наклона которой к оси Х есть характеристическое время релаксации заряда, или постоянная времени RC:

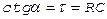. (6.13)

Если обкладки конденсатора попеременно подключать к источнику тока и к сопротивлению R (рис. 6.6), то график процесса заряд-разряд конденсатора будет иметь вид, показанный на рис. 6.7. Процесс заряда-разряда можно наблюдать с помощью осциллографа, подавая на вход Y напряжение с конденсатора C.