Теоретическое введение. Релаксационные колебания – незатухающие негармонические колебания нелинейных систем, для которых характерно накопление и сбрасывание энергии (relaxation –

Релаксационные колебания – незатухающие негармонические колебания нелинейных систем, для которых характерно накопление и сбрасывание энергии (relaxation – ослабление). Их генератором может служить система «газонаполненная лампа-конденсатор» (рис.7.1).

При подключении генератора к источнику e начальное сопротивление незажженной лампы велико, конденсатор С заряжается, одновременно растет разность потенциалов на электродах газонаполненной лампы.

Газы в естественном состоянии состоят из электрически нейтральных атомов и молекул, т.е. не содержат свободных зарядов и поэтому не проводят электрический ток. Проводить они могут, только если часть молекул ионизируется – расщепляется на положительные и отрицательные ионы. Обычно происходит расщепление на одновалентный положительно заряженный ион и электрон. Ионизация может происходить под влиянием различных воздействий на газ, например, нагрева, космических лучей, бомбардировки молекул газа быстро движущимися ионами и электронами (ударная ионизация) и др. (Заметим, что наряду с процессом ионизации в газе происходит и обратный процесс – рекомбинация, т.е. воссоединение положительных и отрицательных ионов в нейтральный атом.)

Так как в обычных условиях газ всегда подвергается действию космических лучей и радиоактивных излучений, то в нем всегда имеются свободные заряды. Однако интенсивность ионизации Δn_i, измеряемая числом пар ионов равного знака, возникающих в единице объема газа в единицу времени, в обычных условиях очень мала и не может обеспечить существенной электропроводности. Поэтому газы ведут себя как изоляторы. Наряду с процессом ионизации в газе происходит и обратный процесс – рекомбинация, т.е. воссоединение положительных и отрицательных ионов в нейтральные атомы. Вероятность такого процесса пропорциональна как числу положительных, так и числу отрицательных ионов. Поэтому количество рекомбинирующих за 1 с в единице объема пар ионов Δn_r пропорционально квадрату имеющихся в единице объема пар ионов:

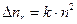, (7.1)

где k – коэффициент рекомбинации.

Под влиянием ионизации и рекомбинации в газе устанавливается равновесное состояние (так называемое динамическое равновесие), когда число пар ионов, возникающих в единичном объеме в единицу времени, равно числу рекомбинирующих пар: 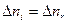. В состоянии равновесия в единице объема газа будет находиться n пар ионов:

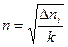(7.2)

Если газ, находящийся под действием внешнего ионизатора, заключен в колбу с впаянными в нее электродами (“лампа”), то при подаче на электроды напряжения через газ потечет ток, который называют газовым разрядом. В этом случае электропроводность газа создается за счет внешнего ионизатора, и ток, возникающий в нем, называется несамостоятельным разрядом. С прекращением действия внешнего ионизатора такой разряд прекращается.

Электрический ток в газе, сохраняющийся после прекращения действия внешнего ионизатора, называется самостоятельным газовым разрядом. Для его осуществления необходимо, чтобы в результате самого разряда в газе непрерывно образовывались свободные заряды.

Плотность электрического тока в газе j (электрический ток, проходящий через единицу площади поперечного сечения) обусловлена движением как положительных, так и отрицательных зарядов:

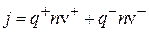, (7.3)

где q⁺ и q^– – величины положительных и отрицательных зарядов; 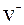и 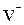– средние квадратичные скорости упорядоченного движения зарядов; n – концентрация зарядов.

Средние скорости упорядоченного движения пропорциональны напряженности электрического поля Е:

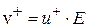; (7.4)

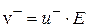. (7.4а)

где 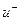и 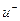– подвижности положительных и отрицательных зарядов (скорости их упорядоченного движения при напряженности электрического поля Е=1 В/м).

Тогда

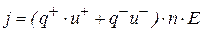. (7.5)

Сравним эту формулу с законом Ома в дифференциальной форме:

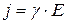; (7.6)

где γ – электропроводность (электропроводимость; проводимость).

Электропроводность будет равна:

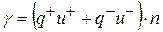. (7.7)

Учитывая, что газы ионизируются, как правило, на электрон и одновалентный положительно заряженный ион, можно записать:

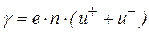. (7.8)

Зависимость тока от приложенного к электродам напряжения называется вольтамперной характеристикой. Она изображена на рис. 7.2. Если к электродам приложить напряжение, то ионы и электроны под действием сил со стороны электрического поля будут двигаться к противоположным электродам. При малых напряжениях (участок 1) концентрация зарядов остается постоянной, так как интенсивность ионизации 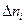будет постоянной, а электродов будет достигать лишь незначительное число заряженных частиц. Поэтому электропроводность также остается постоянной, а сила тока пропорциональна напряженности электрического поля в соответствии с законом Ома (7.6).

С увеличением разности потенциалов (участок 2) линейная зависимость нарушается. Это связано с тем, что под действием электрического поля значительная часть ионов и электронов достигает электродов. Начиная с некоторого значения напряжения (участок 3) ток остается неизменным с увеличением напряжения (I_н – ток насыщения). Это объясняется тем, что все заряды, возникшие в газе под действием внешнего ионизатора, достигают электродов лампы, не успевая рекомбинировать. Поэтому при неизменной интенсивности ионизации не происходит дальнейшего роста тока при увеличении напряжения. Если в объеме трубки V в единицу времени образуется 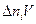пар свободных зарядов и все они приходят на электроды, то ток в трубке будет:

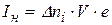(7.9)

где I_н – ток насыщения – максимально возможный ток при данной интенсивности ионизации. Газовый разряд, происходящий на участках 1, 2 и 3 является несамостоятельным газовым разрядом.

При дальнейшем увеличении напряжения (участок 4) происходит резкое увеличение тока. Это объясняется ударной ионизацией: электроны, возникшие в газе за счет внешнего ионизатора, во время своего движения к аноду под действием электрического поля приобретают энергию, достаточную для ионизации нейтральных молекул газа при столкновении с ними. При столкновении образуются вторичные электроны и ионы. В свою очередь вторичные электроны, ускоряясь полем, могут также ионизировать нейтральные молекулы газа.

Число носителей тока лавинообразно возрастает, возрастает и величина тока. Но разряд в газе остается еще несамостоятельным, так как ударная ионизация, вызванная одними электронами, недостаточна для поддержания разряда при удалении внешнего ионизатора. Это вызвано тем, что электроны движутся в электрическом поле от катода к аноду. Поэтому они могут ионизировать только те молекулы газа, которые лежат ближе к аноду по сравнению с местом возникновения данного электрона. Вблизи катода электроны еще не имеют энергии, достаточной для ионизации, и в этой области электроны могут возникать только благодаря внешнему ионизатору.

Если действие ионизатора прекратится, то область ударной ионизации будет постепенно сокращаться, стягиваясь к аноду по мере движения к нему электронов, и в конце концов ударная ионизация и электрический ток в газе прекратятся. Переход от несамостоятельного разряда к самостоятельному становится возможным лишь при таком напряжении между электродами, когда положительные ионы также приобретают энергию, достаточную для ионизации молекул газа, т.е. возникают два встречных потока, каждый из которых способен вызвать ионизацию газа. В этом случае внешний ионизатор не играет существенной роли в осуществлении газового разряда, так как число создаваемых им первоначальных ионов мало по сравнению с числом вторичных ионов, и прекращение действия ионизатора не влияет на протекание разряда.

Опыт показывает, что в большинстве случаев наблюдается не ударная ионизация молекул газа ионами, а выбивание ими электронов с поверхности катода, так как в этом случае работа, совершаемая ионом, меньше, чем при ударной ионизации. Наряду с процессом выбивания ионами электронов из катода – вторичной эмиссией, не менее важным является фотоэффект – выбивание электронов из катода под действием света: достаточно быстрый электрон может не только ионизировать молекулу, но и перевести образовавшийся ион в возбужденное состояние. Переходя затем в устойчивое состояние, ион испускает квант энергии, который способен вызвать фотоионизацию. Испускание света происходит при рекомбинации положительных ионов с электронами – “рекомбинационное свечение”.

Повышая напряжение на электродах, можно возбудить все эти процессы и осуществить переход от несамостоятельного разряда к самостоятельному. Этот переход называется электрическим пробоем газа, а соответствующее напряжение – напряжением зажигания (U_з). Оно зависит от химической природы газа, материала катода, формы электродов и расстояния между ними, давления газа и наличия в нем примесей.

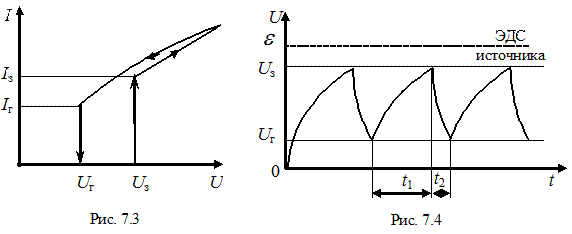
Идеализированная вольтамперная характеристика газонаполненной лампы приведена на рис.7.3. При напряжении U<U_з токи в лампе при обычных внешних ионизаторах малы, и мы их рассматривать не будем

Если увеличивать разность потенциалов на электродах лампы, то при значении U=U_з скачком устанавливается значение тока, равное I_з – лампа “загорается”. При дальнейшем возрастании напряжения ток растет по закону, близкому к линейному.

Если затем уменьшать напряжение на “горящей” лампе, то при напряжении, равном U_з, лампа еще не гаснет. Продолжая уменьшать напряжение, можно увидеть, что лишь при некотором напряжении – напряжении гашения U_г, которое меньше, чем U_з, лампа “гаснет” и ток скачком резко падает. На этом самостоятельный разряд в лампе прекращается. При дальнейшем возрастании напряжения процесс повторяется. Следует заметить, что для реальной лампы зависимость I=f(U) не является линейной, причем при U>U_з кривые, снятые при возрастании и убывании напряжения, не вполне совпадают. Но эти отличия несущественны, и мы можем ими в данной работе пренебречь.

Газонаполненные лампы часто используют для получения релаксационных колебаний. Релаксационные колебания – периодические колебания, по форме резко отличающиеся от синусоидальных и представляющие собой периодически повторяющийся процесс возрастания электрического напряжения и последующего его уменьшения.

Рассмотрим работу генератора релаксационных колебаний. Принципиальная схема представлена на рис. 7.1. Он состоит из источника, дающего постоянное напряжение U₀, конденсатора емкостью С, сопротивления R и лампы Л. Если включить источник, то в цепи появится ток. Сопротивление незажженной лампы бесконечно велико, и ток I_ЗАР будет заряжать конденсатор. Разность потенциалов на его обкладках будет расти. Соответственно растет и разность потенциалов на электродах лампы, подсоединенной параллельно конденсатору. Когда она достигнет значения напряжения зажигания U_з, лампа “зажжется” – ее сопротивление R_Л скачком уменьшится, и она начнет проводить ток. Так как R>>R_Л, то ток разряда конденсатора потечет через лампу. Это вызовет быстрое падение напряжения на конденсаторе, и когда оно достигнет значения напряжения гашения U_г, лампа “гаснет”, и процесс начинается сначала. Возникают релаксационные колебания. Кривая изменения напряжения на конденсаторе представлена на рис. 7.4 и представляет собой негармонические релаксационные колебания. Наблюдая эти колебания на экране осциллографа, можно рассчитать их период: 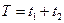; здесь t₁ – время накопления энергии, t₂ – время сброса.

Период релаксационных колебаний в генераторе лампа-конденсатор может быть также определен, если наблюдать на осциллографе фигуры Лиссажу (замкнутые линии, получающиеся при сложении двух взаимно перпендикулярных колебаний). Для этого на одну пару пластин осциллографа подается напряжение с генератора лампа-конденсатор, на другую – переменное напряжение известной частоты от звукового генератора.

Отношение частот колебаний можно определить по виду фигуры Лиссажу, оно равно отношению числа касаний фигуры с прямой, параллельной оси Х и с прямой, параллельной оси Y. На рис. 7.6 (стр.68) показан вид фигуры Лиссажу для соотношения частот 1:1.

Найдем закон, по которому будет меняться напряжение на конденсаторе.

В любой момент времени величина напряжения U₀ равна сумме напряжений в элементах цепи:

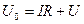; (7.10)

где U – разность потенциалов на обкладках конденсатора.

Заряд конденсатора изменяется вследствие протекания по цепи электрического тока:

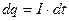; (7.11)

изменение заряда вызывает изменение разности потенциалов:

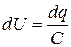. (7.12)

Из уравнений (7.11) и (7.12) находим:

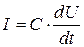. (7.13)

Подставляя (7.13) в (7.10) получаем:

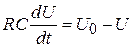. (7.14)

Преобразуем выражение (7.14):

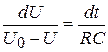(7.15)

и проведем интегрирование:

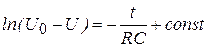. (7.16)

Постоянная интегрирования находится из условия: при t=0 U=0: 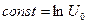. Потенцируя выражение (7.16), получим закон возрастания напряжения на конденсаторе генератора релаксационных колебаний:

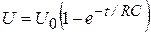. (7.17)

Критическое значение энергии конденсатора

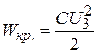. (7.18)