Полупроводники
Определим концентрацию носителей заряда в полупроводнике. Электроны в зоне проводимости и свободные места в валентной зоне возникают в полупроводнике за счет теплового движения решетки кристалла. Вероятность передачи атому энергии eg от тепловых колебаний кристаллической решётки пропорциональна 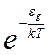 . Скорость образования свободных мест в валентной зоне также пропорциональна этой величине. Свободные места называют "дырками". Это, по сути дела, есть разорванные электронные связи между атомами кристалла. Покинутый электроном атом перестает быть нейтральным, на нем возникает избыточный положительный заряд (+e). Этот заряд приписывается разорванной валентной связи или свободному месту в валентной зоне, то есть введенной фиктивной частице (квазичастице) – дырке. Под действием электрического поля на свободное место в атоме может перейти один из связанных электронов соседних атомов. Эта связь восстановится, но одновременно образуется новая разорванная связь (дырка) в соседнем атоме. То есть движение всей совокупности электронов в почти заполненной валентной зоне полупроводника можно заменить движением пустых мест или квазичастиц – дырок. Электроны в зоне проводимости и дырки в валентной зоне возникают парами, то есть концентрация электронов n равна концентрации дырок: p=n. Скорость их генерации равна
. Скорость образования свободных мест в валентной зоне также пропорциональна этой величине. Свободные места называют "дырками". Это, по сути дела, есть разорванные электронные связи между атомами кристалла. Покинутый электроном атом перестает быть нейтральным, на нем возникает избыточный положительный заряд (+e). Этот заряд приписывается разорванной валентной связи или свободному месту в валентной зоне, то есть введенной фиктивной частице (квазичастице) – дырке. Под действием электрического поля на свободное место в атоме может перейти один из связанных электронов соседних атомов. Эта связь восстановится, но одновременно образуется новая разорванная связь (дырка) в соседнем атоме. То есть движение всей совокупности электронов в почти заполненной валентной зоне полупроводника можно заменить движением пустых мест или квазичастиц – дырок. Электроны в зоне проводимости и дырки в валентной зоне возникают парами, то есть концентрация электронов n равна концентрации дырок: p=n. Скорость их генерации равна
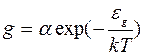 , (5.10)
, (5.10)
где a – коэффициент, различный для разных полупроводников.
Одновременно с генерацией электронно-дырочных пар идет обратный процесс – рекомбинация. При встрече электрон и дырка исчезают, то есть рекомбинируют, восстанавливается разорванная валентная связь, исчезает пустое место в валентной зоне. Скорость рекомбинации r должна быть пропорциональна произведению концентраций электронов и дырок, и так как n=p , то
r=b×n×p=b×n2=b×p2. (5.11)
В состоянии равновесия g=r, тогда
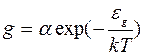 = b n2 = b p2 ,
= b n2 = b p2 ,
а равновесная концентрация
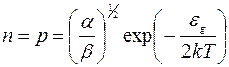 , (5.12)
, (5.12)
или:
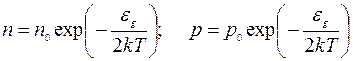 , (5.13)
, (5.13)
где n0 и p0 – концентрации, соответствующие условию T ®¥.
Чистые (беспримесные) полупроводники, в которых равновесные носители заряда возникают за счет переходов электронов из валентной зоны в зону проводимости, называются собственными. Соответственно, для концентрации и проводимости таких полупроводников имеем названия собственная концентрация и собственная проводимость. При этом собственная проводимость обусловлена направленным движением электронов и дырок во внешнем электрическом поле.
В собственном полупроводнике полный ток складывается из тока электронов и тока дырок, концентрации которых одинаковы (n=p):
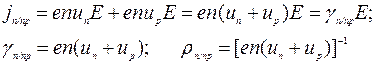 (5.14)
(5.14)
Подвижности электронов и дырок зависят от температуры, но эти слабые зависимости маскируются более сильной температурной зависимостью концентрации носителей (5.13). Поэтому для полупроводника можно записать удельную электропроводимость gп/пр, удельное сопротивление rп/прр и сопротивление Rп/пр следующим образом:
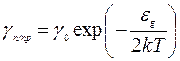 (5.15)
(5.15)
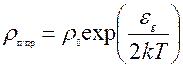 (5.16)
(5.16)
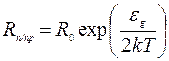 (5.17)
(5.17)
Здесь температура Т в градусах Кельвина; g0, r0 и R0 - значения параметров, полученные при экстраполяции температуры Т®¥. Таким образом, сопротивление полупроводников очень сильно (экспоненциально) зависит от температуры: с ростом температуры резко возрастает концентрация свободных носителей тока – электронов и дырок – при переходе электронов из валентной зоны в зону проводимости за счет энергии теплового движения, поэтому сопротивление полупроводника уменьшается.
 Зависимости (5.15), (5.16) и (5.17), построенные в координатах lngпр=f(1/T), lnrпр=f(1/T) и lnRпр=f(1/T), являются прямыми (рис.5.3).
Зависимости (5.15), (5.16) и (5.17), построенные в координатах lngпр=f(1/T), lnrпр=f(1/T) и lnRпр=f(1/T), являются прямыми (рис.5.3).
По угловому коэффициенту этих прямых можно определить ширину запрещенной зоны (энергию активации eg) полупроводника. Например, для уравнения (5.17) имеем:
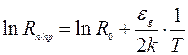 , (5.18)
, (5.18)
откуда получим:
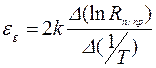 . (5.19)
. (5.19)
Дата добавления: 2015-09-07; просмотров: 875;
