Метод интегрирования по частям

Пусть u = u(х) и v = v(x) - дифференцируемые функции. По свойству дифференциала d(uv) = v du + u dv;

u dv = d(uv) – v du

Интегрируя левую и правую части последнего равенства, получим

ò u dv = uv - ò v du

Выведенная формула называется формулой интегрирования по частям для неопределенного интеграла. При ее применении в подынтегральном выражении в левой части выделяют два сомножителя - u и dv. При переходе к правой части первый сомножитель u дифференцируется (при нахождении du = u'dx), а второй интегрируется (v = ò dv + С). Формулу применяют, если дифференцирование существенно упрощает один из сомножителей (при условии, что интегрирование не слишком усложняет другой).

Пример 1. Например, найдем ò xe^-2xdx. Так как х' = 1, а функция e^-2x при интегрировании практически не изменится (по теореме о линейной подстановке появится лишь постоянный множитель -1/2), то данный интеграл можно найти интегрированием по частям, полагая u = х, dv = e^-2xdx. Найдем v и du:

du = dx

v = ò dv = ò e^-2xdx = (- ½)e^-2x + C

Применяя формулу интегрирования по частям, получим:

ò xe^-2xdx = х ((- ½)e^-2x + C) - ò ((- ½)e^-2x + C)dx

Для нахождения интеграла в правой части применим метод разложения:

ò xe^-2xdx = (- ½)e^-2xх + Cx - (1/4)e^-2x - Cx + C₁ = (- ½)e^-2xх - (1/4)e^-2x + C₁

Замечание. Анализ полученного решения показывает, что постоянная С, возникшая при нахождении v (по заданному dv), не входит в запись окончательного ответа. Можно показать, что и в общем случае постоянная С, возникающая при нахождении v, исключается в процессе решения. Поэтому в дальнейшем, применяя формулу интегрирования по частям и найдя v, будем пренебрегать С для упрощения записи решения.

Пример 2. Найдем .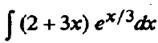

Пример 3. Найдем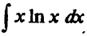

Здесь представлят сложность присутствие логарифма в записи подынтегральной функции. Ее устраняют интегрированием по частям, полагая u = ln х. Тогда dv = x dx (отметим, что при интегрировании функции х получается функция того же типа, т.е. степенная).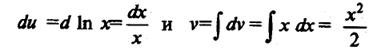

Получим

Пример 4. Найдем .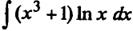

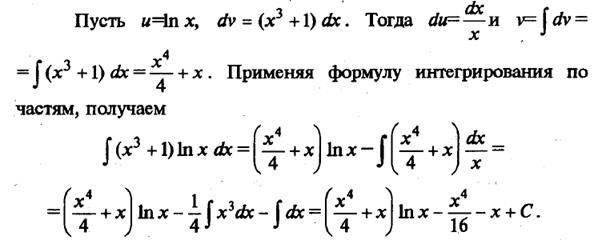
Рассмотрим пример, в котором формулу интегрирования по частям приходится применять более одного раза.

Пример 5. Найдем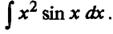

Полученный в результате преобразований интеграл не является табличным, но по сравнению с исходным интегралом степень переменной х в подынтегральном выражении уменышилась на единицу (при этом второй сомножитель cos х того же типа, что и в исходном интеграле). Повторим применение формулы интегрирования по частям (при этом мы избавимся от х и получим табличный интеграл). Положим теперь

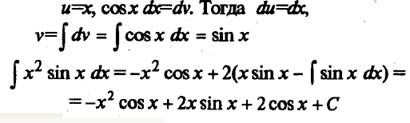
Можно указать следующие основные типы интегралов (но не все), для нахождения которых используется формула интегрирования по частям:

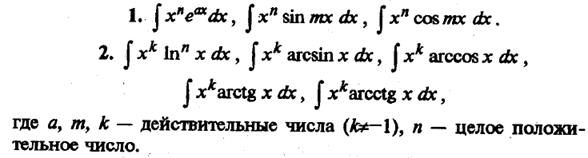
Для нахождения интегралов из первой группы формулу интегрирования по частям применяют n раз. При первом применении полагают u = xⁿ, а остальные сомножители подынтегрального выражения задают dv. Процедуру повторяют, пока степень еременной х не станет равной нулю, а сам интеграл — табличным (см. примеры 1, 2 и 5).

Для нахождения интегралов второй группы полагают x^kdx = dv. Оставшиеся сомножители подынтегрального выражения задают u. При этом если в подынтегральном выражении присутствует n-тая степень логарифма, формулу интегрирования по частям придется применить n раз. После каждого применения эта степень уменьшается на единицу, пока не станет равной нулю, а сам интеграл - табличным.

Метод интегрирования по частям часто комбинируют с другими методами и приемами интегрирования.

Пример 6. Найдем

Выполним сначала замену переменной t = 2x + 3.

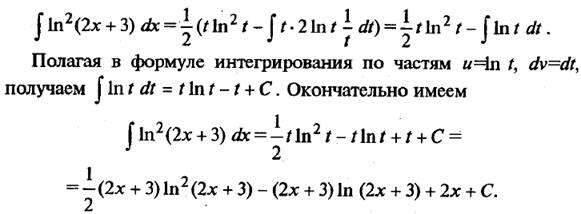
Пример 7. Найдем .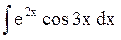

Пусть u = cos 3x, dv = e^2xdx. Тогда du = -3sin 3x dx, v = ½ e^2x.

Искомый интеграл обозначим J («йот»).

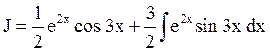
Ко второму слагаемому применим интегрирование по частям еще раз, обозначив u = sin 3x, а dv такой же (dv = e^2xdx). Тогда du = 3cod 3x dx и по-прежнему v = ½ e^2x.

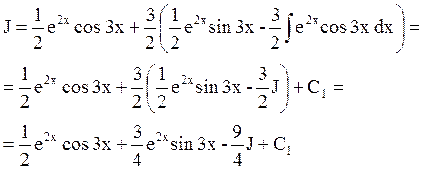
Выразим из полученного уравнения J:

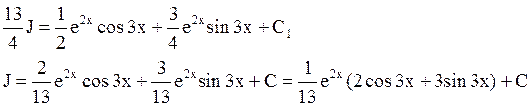
Рассмотренными выше методами далеко не исчерпываются все разработанные методы интегрирования функций. Тем не менее, на их основании можно наметить общий подход к интегрированию функций различных видов.