Методы интегрирования. Рассмотрим некоторые основные методы интегрирования

Рассмотрим некоторые основные методы интегрирования. К ним относятся:

1. Метод разложения (непосредственного интегрирования).

Этот методоснован на непосредственном применении табличных интегралов, а также на применении свойств 4 и 5 неопределенного интеграла (т.е. на выносе за скобку постоянного сомножителя и/или представления подынтегральной функции в виде суммы функций – разложения подынтегральной функции на слагаемые).

Пример 1. Например, для нахождения ò(dx/x⁴) можно непосредственно воспользоваться табличным интегралом для òxⁿdx. В самом деле,
ò(dx/x⁴) = òx^-4dx = x^-3/(-3) + C = -1/3x³ + C.

Рассмотрим еще несколько примеров.

Пример 2. Для нахождения 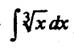воспользуемся тем же интегралом:

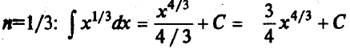
Пример 3. Для нахождения 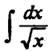надо взять

Пример 4. Чтобы найти 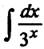, представим подынтегральную функцию в виде 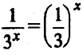и используем табличный интеграл для показательной функции:

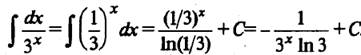
Рассмотрим использование выноса за скобку постоянного сомножителя.

Пример 5. 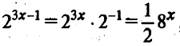Найдем, например 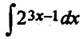. Учитывая, что , получим

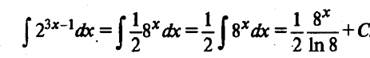
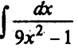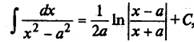Пример 6. Найдем . Поскольку , воспользуемся табличным интегралом Получим

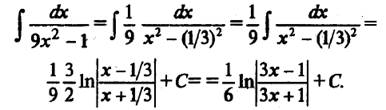
В следующих двух примерах также можно использовать вынос за скобки и табличные интегралы:

Пример 7.

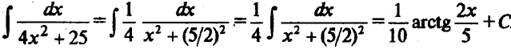
(используем 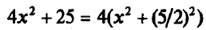и );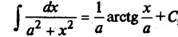

Пример 8.

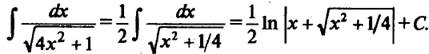
(используем и ).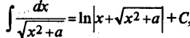

Рассмотрим более сложные примеры, в которых используется интеграл суммы.

Пример 9. Например, найдем 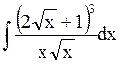. Для применения метода разложения в числителе используем формулу куба суммы*, а затем полученный многочлен почленно разделим на знаменатель.

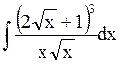= ò ((8x^3/2 + 12x + 6x^1/2 + 1)/(x^3/2))dx = ò (8 + 12x^-1/2 + 6/x + x^-3/2)dx = 8ò dx + 12ò x^-1/2dx +
+ 6ò dx /x + ò x^-3/2dx =

Следует отметить, что в конце решения записана одна общая постоянная С (а не отдельные при интегрировании каждого слагаемого). В дальнейшем также предлагается опускать в процессе решения постоянные от интегрирования отдельных слагаемых до тех пор, пока выражение содержит хотя бы один неопределенный интеграл (будем записывать одну постоянную в конце решения).

Пример 10. Найдем 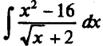. Для решения этой задачи разложим на множители числитель (после этого удастся сократить знаменатель).

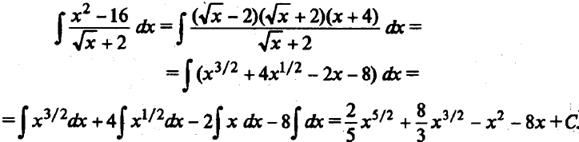
Пример 11. Найдем 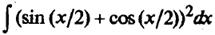. Здесь можно использовать тригонометрические тождества.

Иногда, чтобы разложить выражение на слагаемые, приходится применять более сложные приемы.

Пример 12. Найдем 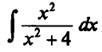. В подынтегральной функции выделим целую часть дроби 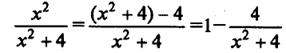. Тогда

.

Пример 13. Найдем