Свойства неопределенного интеграла

Рассмотрим без доказательства основные свойства неопределенного интеграла.

1. Производная от неопределенного интеграла равна подынтегральной функции, т.е. (ò f(x)dx)` = f(x).

2. Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е. d(ò f(x)dx) = f(x)dx.

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.
ò dF(x) = F(x) + C.

Сравнивая между собой свойства 2 и 3, можно сказать, что операции нахождения неопределенного интеграла и дифференциала взаимнообратны (знаки d и ò взаимно уничтожают друг друга, в случае свойства 3, правда, с точностью до постоянного слагаемого).

4. Постоянный множитель можно выносить за знак интеграла, т.е.
ò C*f(x)dx = C*ò f(x)dx.

5. Интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций, т.е. ò (f₁(x) + f₂(x))dx = ò f₁(x)dx + ò f₂(x)dx (это свойство остается справедливым для любого конечного числа слагаемых).

Список («таблица») основных интегралов

Перечислим интегралы от элементарных функций, которые иногда называют табличными:

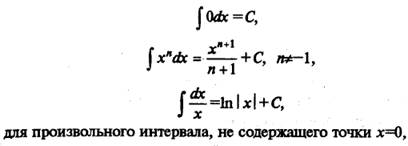
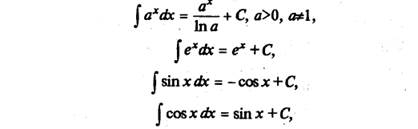
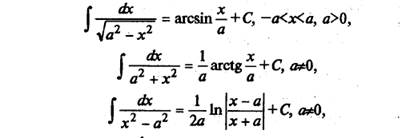
Любую из приведенных выше формул можно доказать, взяв производную от правой части (в результате будет получены подынтегральная функция).